[PYTHON] [Statistik] Visualisieren und verstehen Sie die Hamiltonsche Monte-Carlo-Methode mit Animation.

In diesem Artikel wird versucht, das Funktionsprinzip der Hamilton-Monte-Carlo-Methode (HMC) mithilfe von Animationen zu verstehen. Dies ist eine Fortsetzung des Artikels des anderen Tages: "[Statistik] Ich werde das Sampling mit der Markov-Ketten-Monte-Carlo-Methode (MCMC) mit Animation erläutern."](Http://qiita.com/kenmatsu4/items/55e78cc7a5ae2756f9da).

Ich habe das Beispiel von Professor Toyodas Buch "Bayes Statistics from the Basics" verwendet. Die zu untersuchende Verteilung ist diesmal die Gammaverteilung. Dieser Artikel enthält nur eine theoretische Erläuterung der für die Animation verwendeten Teile. Eine ausführliche Erläuterung der HMC finden Sie in diesem Buch.

Einführung

Das zu schätzende Ziel ist die Gammaverteilung mit $ \ theta $ als Variable. Da die durch die Bayes'sche Schätzung zu schätzenden Parameter durch $ \ theta $ dargestellt werden, werden sie als Verteilung von $ \ theta $ dargestellt. [^ 1]

[^ 1]: Die Gammaverteilung ist eine relativ einfache Verteilung, die so wie sie ist ausreichende Informationen liefern kann, aber hier werden wir annehmen, dass dies eine schwierige hintere Verteilung war. Aus dieser posterioren Verteilung werden wir mit HMC Zufallszahlen generieren und versuchen, die Informationen der posterioren Verteilung aus der erhaltenen Zufallszahlenfolge herauszufinden.

Hier ist die Gammaverteilung. $ f(\theta|\alpha, \lambda) = {\lambda^{\alpha} \over \Gamma(\alpha)} \theta^{\alpha-1}e^{-\lambda \theta} \quad \quad 0 \le x,\quad 0 < \lambda,\quad 0 < \alpha $

Konzentrieren Sie sich nur auf den Kernel-Teil dieser Gamma-Verteilung ohne die Normalisierungskonstante. $ f(\theta|x) \propto e^{-\lambda \theta} \theta ^{\alpha -1} $ Es wird sein.

In der HMC wird dies protokolliert und mit Minus multipliziert $h(\theta) = -\log (f(\theta|x)) = \lambda \theta - (\alpha -1) \log(\theta) $ Entspricht der Positionsenergie in der Physik. Dieses Mal verwenden wir $ \ alpha = 11, \ lambda = 13 $ für die Parameter. Die Grafik sieht wie folgt aus.

Hamiltonian abgeleitet aus der Beziehung zwischen Positionsenergie $ h (\ theta) $ und kinetischer Energie $ p $ $H(\theta, p) = h(\theta) + {1 \over 2} p^2$ In Anbetracht der Eigenschaft, dass es konstant wird, wenn keine externe Kraft angewendet wird, nimmt die kinetische Energie jedoch zu, wenn die Positionsenergie abnimmt. Die obige Abbildung ist eine Animation dieser Situation. Die Länge des roten Pfeils gibt die Größe der kinetischen Energie $ p $ an.

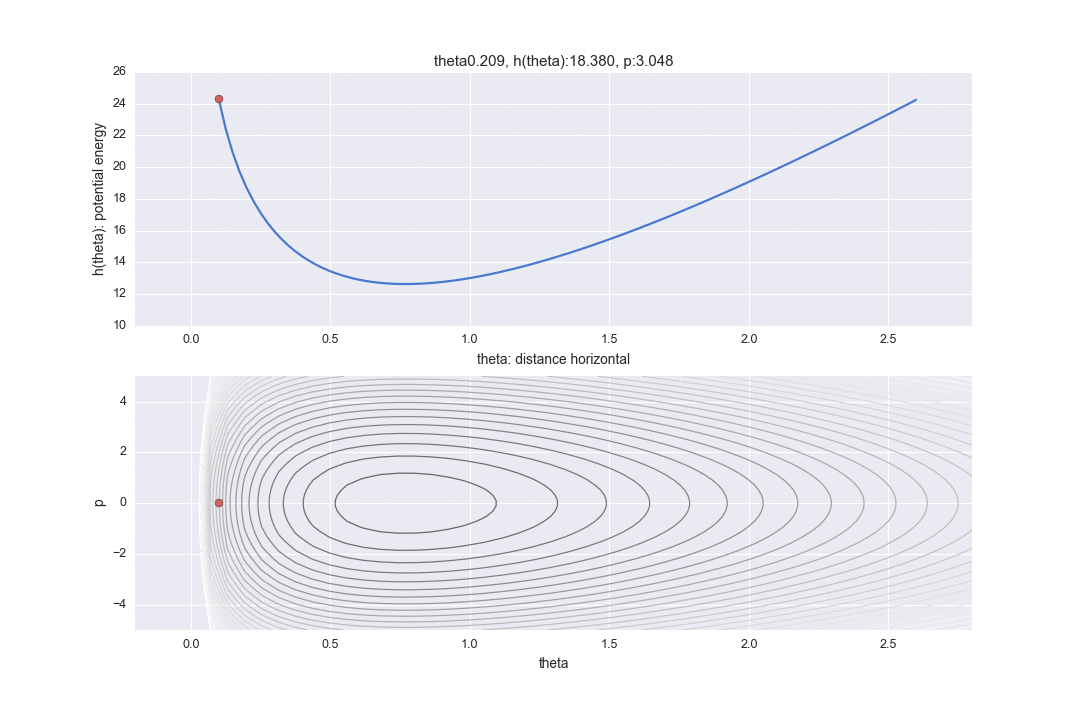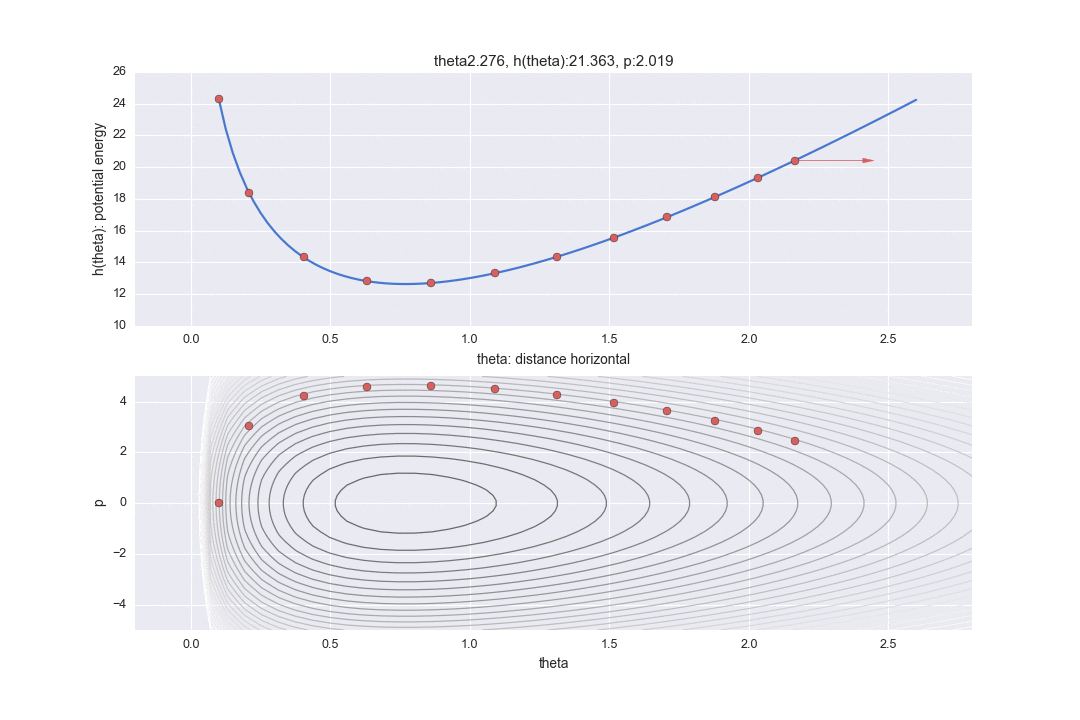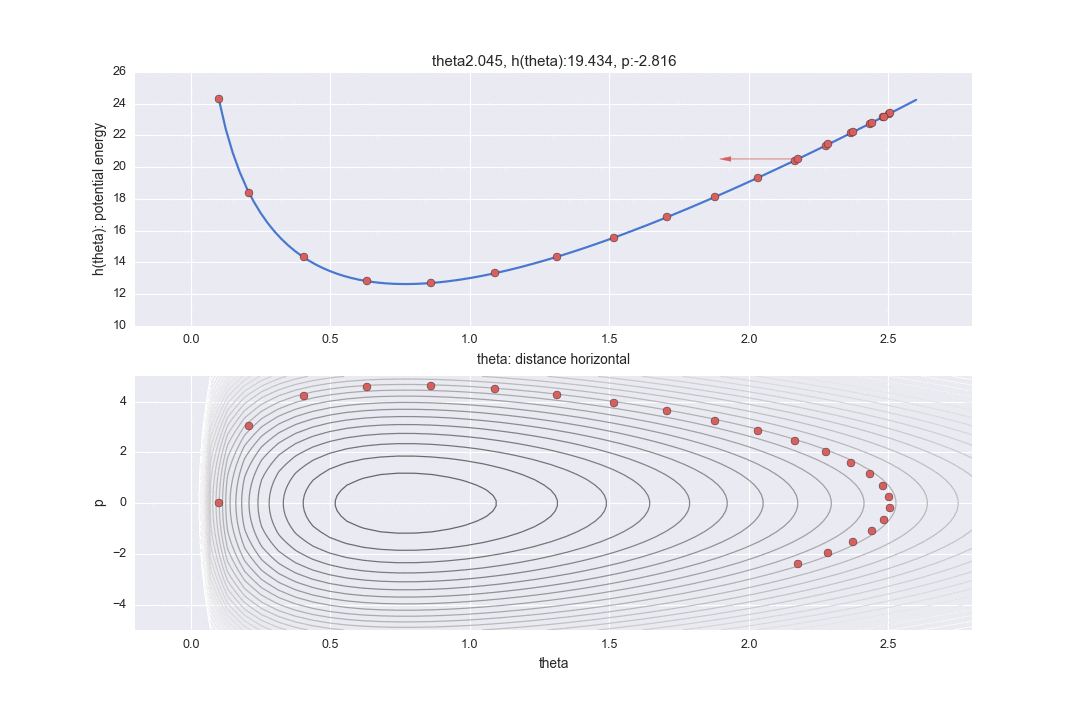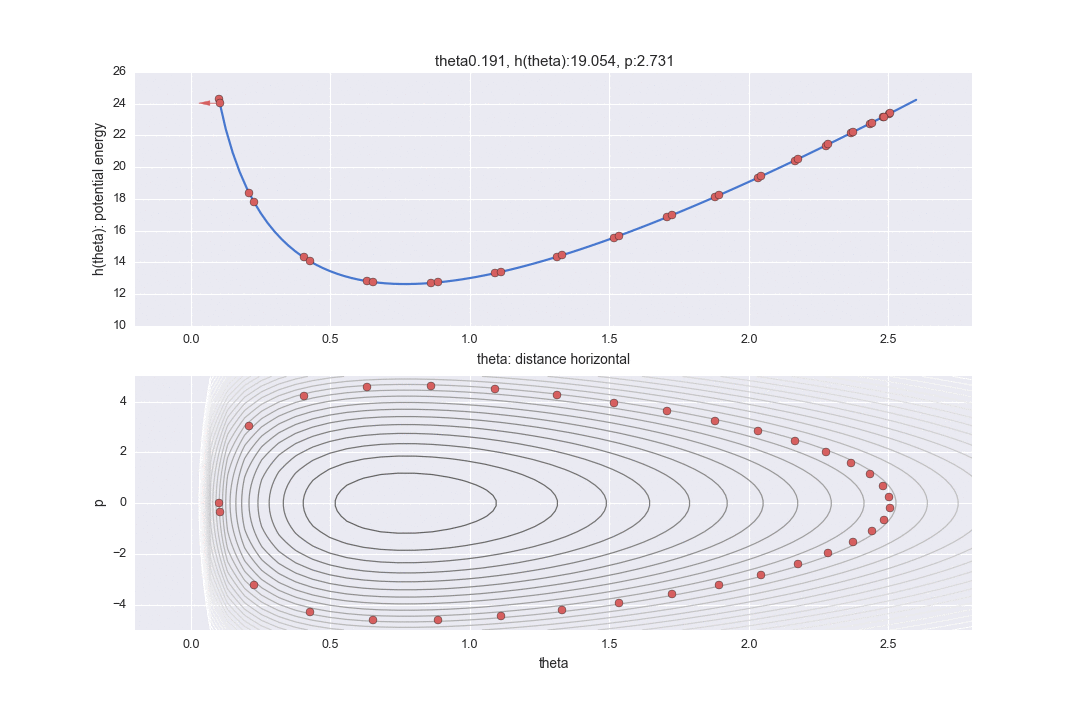
Außerdem ist der Graph im unteren Teil ein Graph eines sogenannten Phasenraums, wobei die horizontale Achse den horizontalen Abstand $ \ theta $ und die vertikale Achse die kinetische Energie $ p $ darstellt. (Im Gegensatz zu Lehrbüchern wird die Figur vertikal und horizontal invertiert, um die horizontale Achse an der obigen Grafik auszurichten.) Die Konturlinie zeigt den Teil, in dem der Hamilton-Wert konstant ist. Unter der Voraussetzung, dass Hamiltonian konstant ist, wird es daher in zwei Anzeigemethoden gezeigt, der entsprechenden horizontalen Position und der Ansicht, dass die kinetische Energie unterschiedlich ist.

Sprungfroschmethode

Wie in der obigen Abbildung gezeigt, wird die Leapfrog-Methode als Methode zur numerischen Berechnung des Hamilton-Operators verwendet, damit er sich an einer bestimmten Stelle bewegt. Einzelheiten zur Theorie finden Sie im Buch, aber hier werde ich den Python-Code veröffentlichen. Es ist eine Methode, um den Fehler aufgrund numerischer Berechnungen zu reduzieren, indem die Position neben $ p $ in zwei Hälften berechnet wird.

# function definitions

def h(theta):
    global lam, alpha
    return lam * theta - (alpha-1)*np.log(theta) 

def dh_dtheta(theta):
    global lam, alpha
    return lam - (alpha - 1)/theta

def hamiltonian(p, theta):
    return h(theta) + 0.5*p**2

vhamiltonian = np.vectorize(hamiltonian)  # vectorize

def leapfrog_nexthalf_p(p, theta, eps=0.01):
    """
    1/Berechnen Sie p nach 2 Schritten
    """
    return p - 0.5 * eps* dh_dtheta(theta)

def leapfrog_next_theta(p, theta, eps=0.01):
    """
Berechnen Sie θ nach einem Schritt
    """
    return theta + eps*p


def move_one_step(theta, p, eps=0.01, L=100, stlide=1):
    """
Führen Sie einen Schritt aus, der L-mal mit der Sprungfroschmethode verschoben wurde
    """
    ret = []
    ret.append([1, p, theta, hamiltonian(p,theta)])
    for _ in range(L):
        p = leapfrog_nexthalf_p(p, theta, eps)
        theta = leapfrog_next_theta(p, theta, eps)
        p = leapfrog_nexthalf_p(p, theta, eps)
        ret.append([1, p, theta, hamiltonian(p,theta)])
    return ret[::stlide]

#Ausführung der Schaltfroschmethode
# initial param
theta = 0.1
p = 0
eps = 0.05
L = 96

result = move_one_step(theta, p, eps=eps, L=100, stlide=1)

Übergang nach der Sprungfroschmethode und Änderung des Impulses p durch Standardnormalverteilung

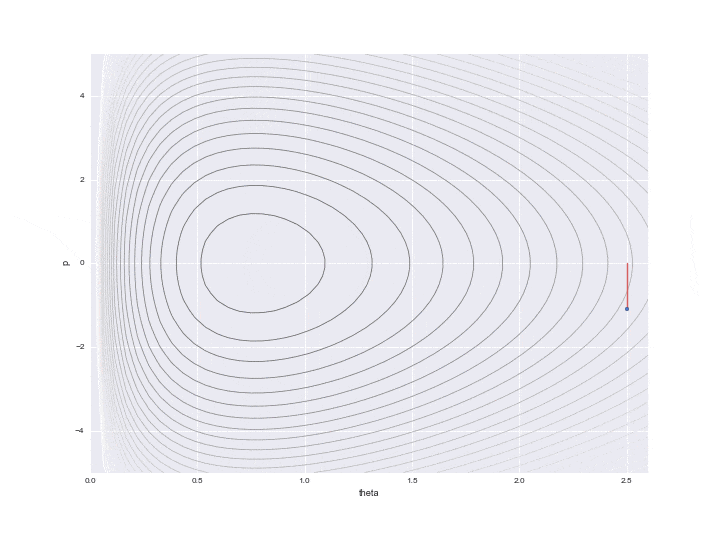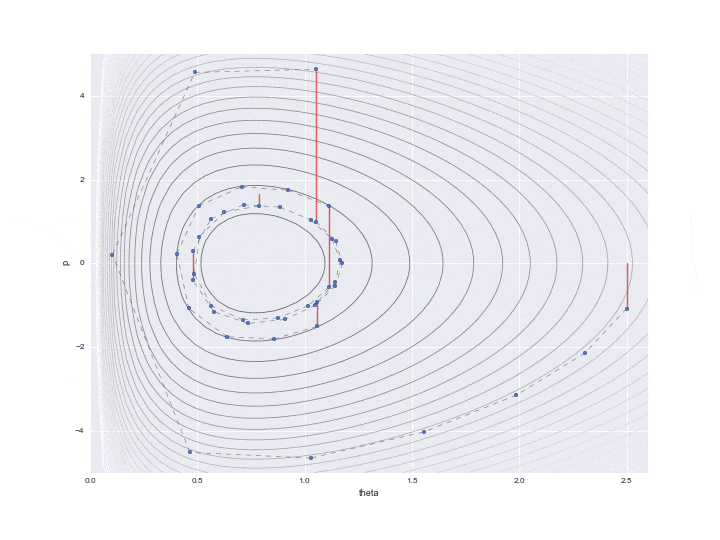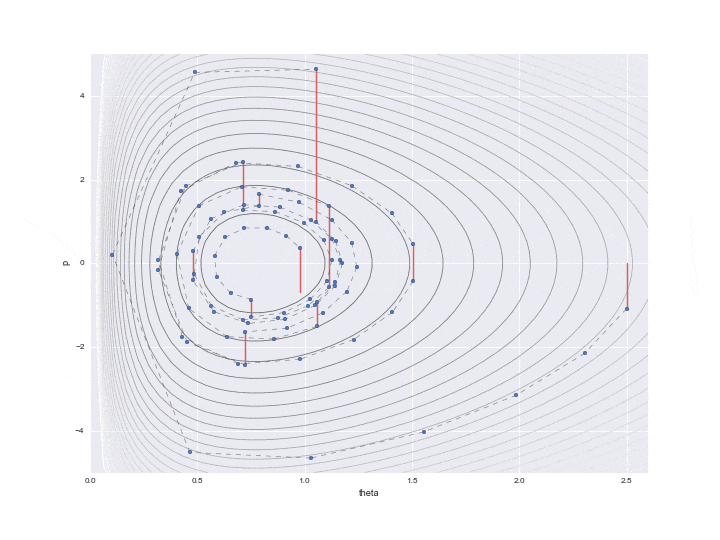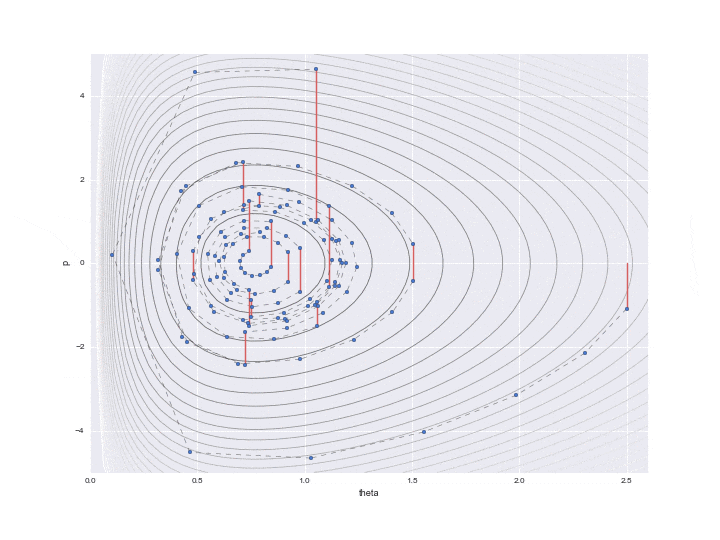
Der durch $ L $ angegebene Übergang wird durch die gepunktete Linie in der folgenden Grafik angezeigt. Es war schwierig, alle L-Trajektorien zu schreiben, deshalb habe ich 12 davon übersprungen. In Wirklichkeit bewegen sich die Punkte also feiner.

Zusätzlich wird in der Mitte eine rote Linie angezeigt, was bedeutet, dass die Positionsenergie nach dem Übergang L einmal zufällig geändert wurde. Speziell

p = rd.normal(loc=0,scale=scale_p)       # ------(*)

$ P $ wird mit einer Zufallszahl aktualisiert, die der durch den Code dargestellten Standardnormalverteilung folgt. (Ich verstehe nicht, warum hier die Normalverteilung ** "Standard" ** verwendet wird. Es scheint nicht schlecht zu sein, die Varianz als Parameter anpassen zu können ... Wenn jemand weiß, lassen Sie es mich bitte wissen ... Zu diesem Zeitpunkt ist die Erhaltung des Hamilton-Werts unterbrochen, und die Konturlinien verschiedener Hamilton-Werte werden erneut L-mal verschoben. Nur ein Punkt kurz vor dem Zeichnen dieser roten Linie wird tatsächlich für die Abtastung verwendet, und die verbleibenden Werte werden einfach als Werte in der Mitte der Berechnung verworfen.

rd.seed(123)
theta = 2.5
eps = 0.01
T = 15

step = []
prev_p = 0

for tau in range(T):
    p = rd.normal(loc=0,scale=scale_p)       # ------(*)
    step.append([2, p, prev_p, 0])
    one_step = move_one_step(theta, p, eps=eps, L=96, stlide=12)
    theta = one_step[-1][2]
    step.extend(one_step)
    prev_p = one_step[-1][1]

    
print len(step)

def animate(nframe):
    global num_frame, n
    sys.stdout.write("{}, ".format(nframe))
    
    if step[n][0] == 1:
        plt.scatter(step[n][2], step[n][1], s=20, zorder=100)
        if step[n-1][0] == 1:
            plt.plot([step[n-1][2], step[n][2]],[step[n-1][1], step[n][1]], c="k", ls="--", lw=.8, alpha=0.5)
        
    else:
        theta = step[n+1][2]
        
        plt.plot([theta, theta], [step[n][2], step[n][1]], c="r")
        
    n += 1
    
    
num_frame = len(step)-1
n = 0
scale_p = 1
fig = plt.figure(figsize=(12,9))

xx = np.linspace(0.01, 2.6)
yy = np.linspace(-5,5)
X, Y = np.meshgrid(xx, yy)
Z = vhamiltonian(Y, X)
plt.contour(X, Y, Z, linewidths=1, cm=cm.rainbow, levels=np.linspace(0,40,40))

plt.ylabel("p")
plt.xlabel("theta")
plt.xlim(0,2.6)
plt.ylim(-5,5)

anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('hmc_sampling_detail.gif', writer='imagemagick', fps=5, dpi=60)

Probenahme

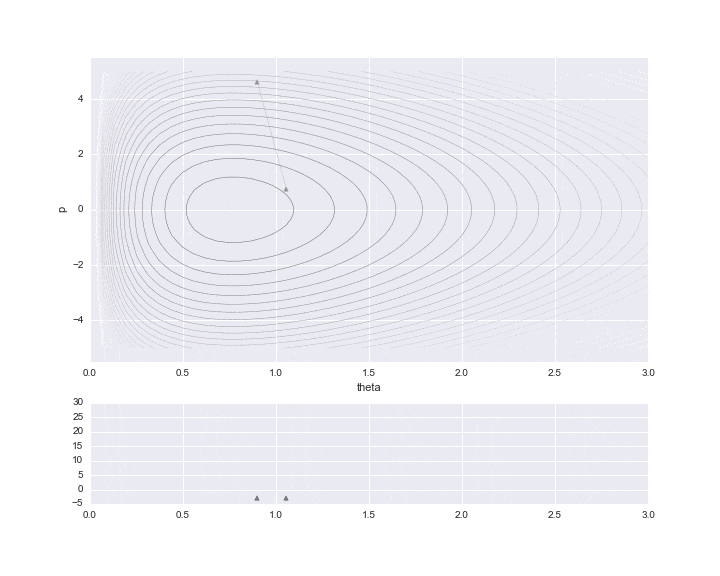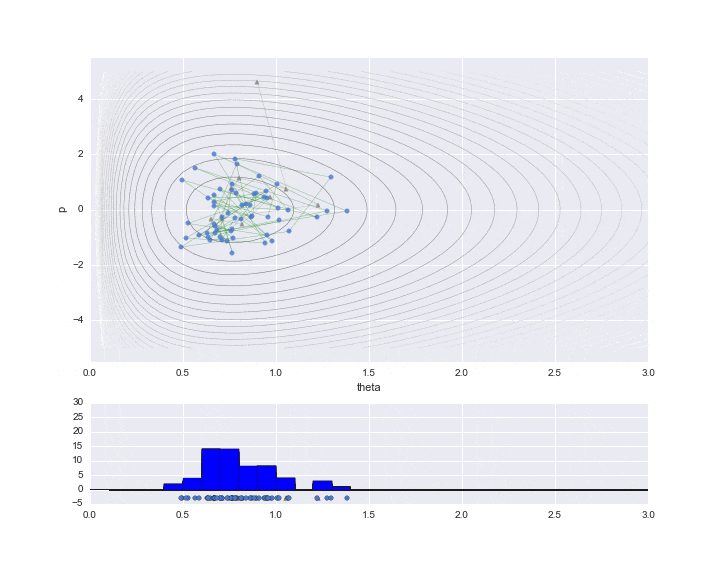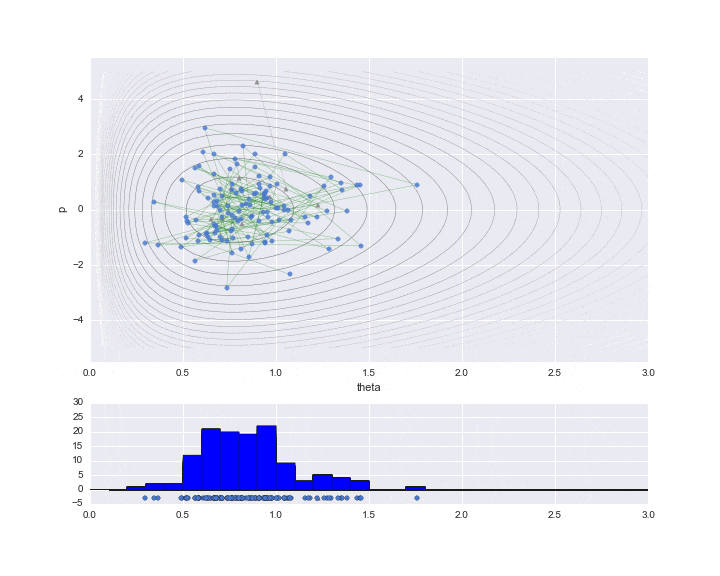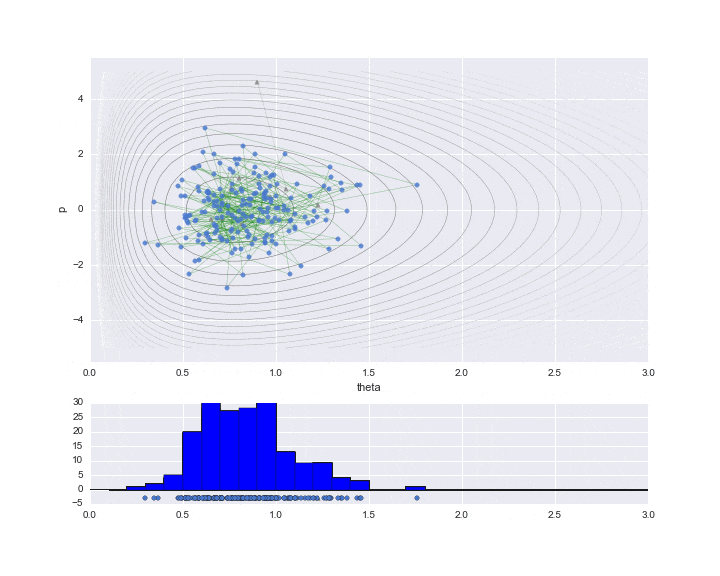
Unten sehen Sie das Ergebnis des Zeichnens nur der Daten, die tatsächlich benötigt werden.

Ebenfalls,

Um die Akzeptanzrate als $ \ min (1, r) $ zu sein

r = np.exp(prev_hamiltonian-H)       # -----(**)

Und rd.uniform () werden verglichen, um Akzeptanz und Nichtakzeptanz zu bestimmen. In diesem Beispiel wurde es jedoch nie abgelehnt, sodass alles akzeptiert wird. Die Einbrennzeit ist auf 10 eingestellt, und die Abtastwerte werden während dieser Zeit durch ▲ angezeigt. Das untere Diagramm ist ein Histogramm des zu schätzenden Wertes von $ \ theta $. Wir haben nur etwas weniger als 200 abgetastet, aber wir können sehen, dass es sich um ein Histogramm der Verteilungsform handelt, wie die nach rechts verzerrte Gammaverteilung.

# HMC simulation
rd.seed(71)
scale_p = 1

# initial param
theta = 2.5
p = rd.normal(loc=0,scale=scale_p)
eps = 0.01
L = 100
T = 10000
sim_result = []
prev_hamiltonian = hamiltonian(p,theta)
sim_result.append([ p, theta, prev_hamiltonian, True])
for t in range(T):
    prev_p = p
    prev_theta = theta
    prev_hamiltonian = hamiltonian(p,theta)
    for i in range(L):
        p = leapfrog_nexthalf_p(p, theta, eps=eps)
        theta = leapfrog_next_theta(p, theta, eps=eps)
        p = leapfrog_nexthalf_p(p, theta, eps=eps)

    H = hamiltonian(p,theta)
    r = np.exp(prev_hamiltonian-H)       # -----(**)
    if  r > 1:
        sim_result.append([ p, theta, hamiltonian(p,theta), True])
    elif r > 0 and rd.uniform() < r:
        sim_result.append([ p, theta, hamiltonian(p,theta), True])
    else:
        sim_result.append([ p, theta, hamiltonian(p,theta), False])
        theta = prev_theta
    
    p = rd.normal(loc=0,scale=scale_p)
    
sim_result = np.array(sim_result)
df = pd.DataFrame(sim_result, columns="p,theta,hamiltonian,accept".split(","))
#df
print "accept ratio: ", np.sum([df.accept == 1])/len(df)

Die Akzeptanz liegt nahe bei 100%: Lächeln:

out

accept ratio:  0.999900009999

Hier ist der Code, der die Animation bis zu T = 200 generiert hat.

def animate(nframe):
    global num_frame, n
    sys.stdout.write("{}, ".format(nframe))
     
    ####Obere Reihe#####
    if n < burn_in:
        marker = "^"
        color  = "gray"
        lc     = "gray"
    else:
        marker = "o"
        color  = "b"
        lc     = "green"

    if sim_result[i,3]  == 0:
        marker = "x"
        color  = "r"
        lc     = "gray"

    axs[0].scatter(sim_result[n,1], sim_result[n,0], s=20, marker=marker, 
                   zorder=100, alpha=0.8, color=color) #,

    if n > 1:
        axs[0].plot([sim_result[n-1,1], sim_result[n,1]],
                    [sim_result[n-1,0], sim_result[n,0]], c=lc, lw=0.5, alpha=0.4)

        
    ####Untere Reihe#####
    axs[1].scatter(sim_result[n,1], -3, alpha=1, marker=marker, c=color)

    if n > burn_in:
        hist_data = pd.DataFrame(sim_result[burn_in:n], columns="p,theta,hamiltonian,accept".split(","))
        hist_data = hist_data[hist_data.accept ==1]
        hist_data.theta.hist(bins=np.linspace(0,3,31),ax=axs[1], color="blue",)
    ### ========================
    
    n += 1
    
burn_in = 10
num_frame = 200
n = 1
n_col = 1
n_row = 2

fig, _ = plt.subplots(n_row, n_col, sharex=False, figsize=(10,8)) 
gs = gridspec.GridSpec(n_row, n_col, height_ratios=[3,1])
axs = [plt.subplot(gs[i]) for i in range(n_row*n_col)]

xx = np.linspace(0.01, 3)
yy = np.linspace(-5,5)
X, Y = np.meshgrid(xx, yy)
Z = vhamiltonian(Y, X)
axs[0].contour(X, Y, Z, linewidths=0.5, cm=cm.rainbow, levels=np.linspace(0,40,40))
    
axs[0].set_ylabel("p")
axs[0].set_xlabel("theta")
axs[0].set_xlim(0,3)
axs[1].set_xlim(0,3)
axs[1].set_ylim(-5,30)
    
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('hmc_simulation2.gif', writer='imagemagick', fps=4, dpi=72)

Vollständige Probenahme

Bis zu dem oben Gesagten wurde T für die Animation auf einen kleinen Wert von 200 eingestellt, aber hier ist eine Darstellung aller T = 10000. Das Einbrennen wird mit 1000 angegeben.

Ein Trace-Plot von $ \ theta $. Der graue Teil in der ersten Hälfte ist der Einbrennteil.

Hier ist ein Histogramm der Ergebnisse. Wenn Sie es mit der Gammaverteilung von $ \ alpha = 11, \ lambda = 13 $ vergleichen, können Sie sehen, dass sie fast gleich sind: grinsen:

abschließend

Es wurde gesagt, dass die Verwendung der Hamilton-Monte-Carlo-Methode die Akzeptanzrate der Probenahme erhöhen würde, aber es wurde festgestellt, dass die Akzeptanzrate sicherlich hoch war (diesmal fast 100%): zufrieden:

Referenz

"Bayes-Statistik aus den Grundlagen - Eine praktische Einführung in die Hamilton-Monte-Carlo-Methode -" (herausgegeben von Hideki Toyoda) https://www.asakura.co.jp/books/isbn/978-4-254-12212-1/

Vollständiger Code für diesen Artikel https://github.com/matsuken92/Qiita_Contents/blob/master/Bayes_chap_05/HMC_Gamma-for_Publish.ipynb (Empfohlenes Surfen auf dem PC, bitte im Desktop-Modus auf dem Smartphone surfen.)

Einstellungen zum Generieren animierter GIFs aus Python auf dem Mac http://qiita.com/kenmatsu4/items/573ca0733b192d919d0e

Einführung in die Bayes'sche Statistik aus den Grundlagen http://stats-study.connpass.com/event/27129/ → Dies ist eine Lernsitzung für dieses Buch, das ich hoste.