[PYTHON] Du kannst es sehen! Vergleich der Optimierungsmethoden (2020)
Zielperson
Für diejenigen, die einen Vergleich jeder Optimierungsmethode sehen möchten. Vergleichen wir die in hier eingeführten Methoden in verschiedenen Suchbereichen. Wenn Sie eine andere gute Suchebene haben oder einen Suchraum haben, den Sie ausprobieren möchten, warten wir auf Informationen.
Inhaltsverzeichnis
- x^2-y^2
- tanh(x)^2+tanh(y)^2
- -sin(x)/x-sin(y)/y+(x^2+y^2)/7
- [Hochwertige Version](# Hochwertige Version)
- [Verwendeter Code](# Verwendeter Code)
x^2-y^2 Vorerst
f(x, y) = x^2 - y^2
Lassen Sie uns nach dem Ursprung suchen.
Die Anfangsposition ist $ (x_0, y_0) = (-1,5, -10 ^ {-4}) $. Die $ y $ -Koordinate ist nicht 0, da die Lernregeln Dinge enthalten, die nicht davon ausgehen, dass die Neigung vollständig $ 0 $ beträgt.
Nun, es ist in Ordnung zu sagen, dass der Gradient nicht vollständig $ 0 $ ist.


 Es gibt viele Lernregeln, die nicht vom Sattel erfasst werden, da es in Richtung der $ y $ -Achse einen leichten Gradienten gibt. Die Lernregeln, die gefangen werden, werden irgendwann fallen.
Übrigens sieht es so aus, wenn es komplett Null ist.
Es gibt viele Lernregeln, die nicht vom Sattel erfasst werden, da es in Richtung der $ y $ -Achse einen leichten Gradienten gibt. Die Lernregeln, die gefangen werden, werden irgendwann fallen.
Übrigens sieht es so aus, wenn es komplett Null ist.
 Der Weihnachtsmann verdunstet augenblicklich, und die Lernregel, die auch dann keine Rolle spielt, wenn der Gradient vollständig Null ist, wird vollständig im Sattelpunkt erfasst. SMORMS3 funktioniert nicht mehr mit einem Ruck. Möglicherweise liegt ein Fehler im Code vor ...
Der Weihnachtsmann verdunstet augenblicklich, und die Lernregel, die auch dann keine Rolle spielt, wenn der Gradient vollständig Null ist, wird vollständig im Sattelpunkt erfasst. SMORMS3 funktioniert nicht mehr mit einem Ruck. Möglicherweise liegt ein Fehler im Code vor ...
tanh(x)^2+tanh(y)^2 Nächster
f(x, y) = \tanh^2 x + \tanh^2 y
Also habe ich es an der Anfangsposition $ (x, y) = (-1, 2) $ versucht.
Immerhin passt nur SMORMS3 in den Sattelpunkt ...
Der Weihnachtsmann ist irgendwohin gegangen, aber Sie können sehen, dass er zurückkommt.



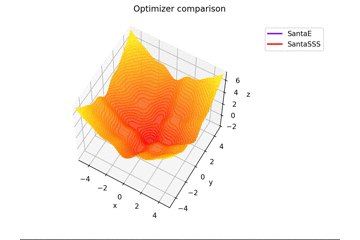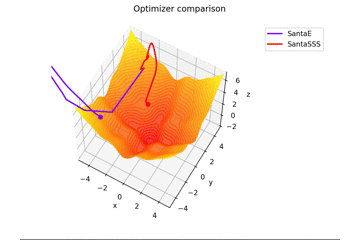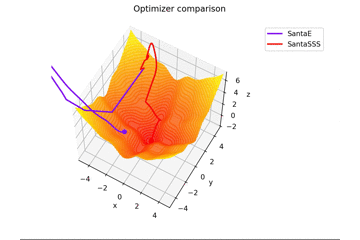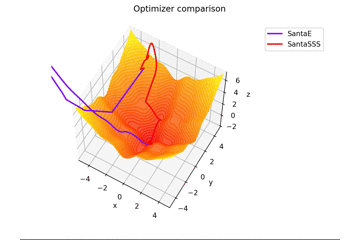
-sin(x)/x-sin(y)/y+(x^2+y^2)/7 fortsetzen
f(x, y) = -\cfrac{\sin (\pi x)}{\pi x} - \cfrac{\sin (\pi y)}{\pi y} + \cfrac{x^2+y^2}{7}
ist. Dies unterscheidet sich von den anderen in $ x, y \ in [-5, 5] $ und die Anfangsposition ist $ (x, y) = (-3, 4) $. $ \ Frac {x ^ 2 + y ^ 2} {7} $ wird hinzugefügt, um eine Lernregel zu erstellen, die genau zum Sattel passt, und eine Lernregel, die nicht passt.


 In Bezug auf $ N $ in Santas Lernregel hatte ich, soweit ich die Zeitung las, das Gefühl, dass es die Anzahl der Mini-Batches war, also habe ich $ N = 1 $ gesetzt, aber wenn $ N = 16 $, wird es fest konvergieren. richtig...
Übrigens vibriert es, wenn $ N = Epoche $.
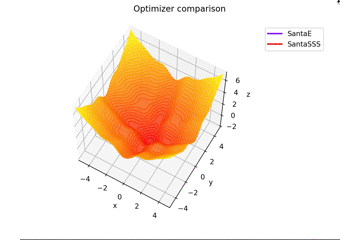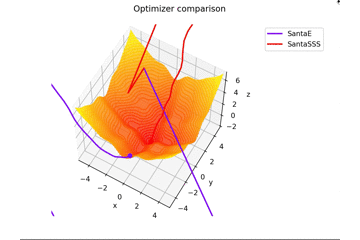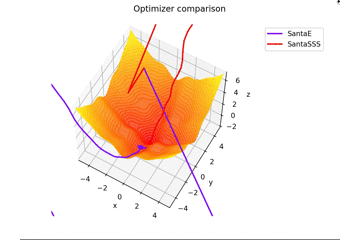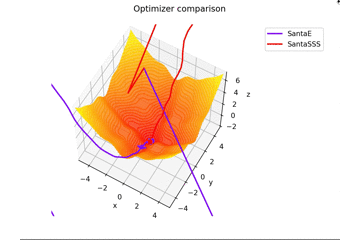
Ich werde es nicht sagen, aber wenn Sie $ epoch $ erhöhen und $ N = epoch $ setzen, wird es wie ein Gemälde aussehen lol
Immerhin sollte es als die Anzahl der Mini-Batch erkannt werden. Praktisch ist $ N = 16,32 $ und bei diesem Wert vibriert es leicht.
In Bezug auf $ N $ in Santas Lernregel hatte ich, soweit ich die Zeitung las, das Gefühl, dass es die Anzahl der Mini-Batches war, also habe ich $ N = 1 $ gesetzt, aber wenn $ N = 16 $, wird es fest konvergieren. richtig...

Übrigens vibriert es, wenn $ N = Epoche $.

Ich werde es nicht sagen, aber wenn Sie $ epoch $ erhöhen und $ N = epoch $ setzen, wird es wie ein Gemälde aussehen lol
Immerhin sollte es als die Anzahl der Mini-Batch erkannt werden. Praktisch ist $ N = 16,32 $ und bei diesem Wert vibriert es leicht.
Hochwertige Version
Die Bildqualität ist rauer als ich erwartet hatte, daher werde ich eine kleine, qualitativ hochwertige Version hinterlassen.
 Das Kapazitätslimit, das geschlossen wurde ...
Das Kapazitätslimit, das geschlossen wurde ...
Code verwendet
Hier ist der experimentelle Code. Wenn ich eine Animation mit einem Jupyter-Notizbuch ausgebe, werden Punkte und Linien unterhalb der Suchebene angezeigt und sind schwer zu erkennen. Daher führe ich sie auf dem Terminal aus.
Experimenteller Code
test.py
#%matplotlib nbagg #Für Jupiter
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from mpl_toolkits.mplot3d import Axes3D
from optimizers import * #Kommentar zu jupyter
#Es wird davon ausgegangen, dass sich das Optimierungsmodul im selben Ordner befindet.
def g(x, y):
#return (x**2 - y**2) * 1
#return np.tanh(x)**2 + np.tanh(y)**2
return -(np.sinc(x) + np.sinc(y)) + (x**2 + y**2)/7
def dgx(x, y):
#return 2*x * 1
#return 2 * np.tanh(x) / np.cosh(x)**2
return np.sin(np.pi*x)/(np.pi * x**2) + 2*x/7 - np.cos(np.pi*x)/x
def dgy(x, y):
#return -2*y * 1
#return 2 * np.tanh(y) / np.cosh(y)**2
return np.sin(np.pi*y)/(np.pi * y**2) + 2*y/7 - np.cos(np.pi*y)/y
num = 401
#x = np.linspace(-2, 2, num)
#y = np.linspace(-2, 2, num)
x = np.linspace(-5, 5, num)
y = np.linspace(-5, 5, num)
X, Y = np.meshgrid(x, y)
Z = g(X, Y)
elevation = np.arange(np.min(Z), np.max(Z), 0.25)
#start_x = -1.5
#start_y = -1e-4
#start_x = -1
#start_y = 2
start_x = -3
start_y = 4
exact_x = 0
exact_y = 0
epoch = 500
N = epoch
seed=2
np.random.seed(seed=seed)
#fig = plt.figure()
#ax = fig.add_subplot(111, projection="3d")
#ax.set_zlim(-1, 1)
#im = ax.plot_surface(X, Y, Z, cmap="autumn")
#fig.show()
opt_dict = {
# "SDG": SGD(eta=5e-2),
# "MSGD": MSGD(eta=5e-2),
# "NAG": NAG(eta=5e-2),
# "AdaGrad": AdaGrad(eta=1e-1),
# "RMSprop": RMSprop(eta=5e-2),
# "AdaDelta": AdaDelta(),
# "Adam": Adam(alpha=5e-2),
# "RMSpropGraves": RMSpropGraves(eta=1e-2),
# "SMORMS3": SMORMS3(eta=1e-2),
# "AdaMax": AdaMax(alpha=2e-2),
# "Nadam": Nadam(alpha=2e-2),
# "Eve": Eve(alpha=5e-2),
"SantaE": SantaE(eta=1e-3, burnin=10, N=N),
"SantaSSS": SantaSSS(eta=1e-3, burnin=10, N=N),
# "AMSGrad": AMSGrad(alpha=5e-2),
# "AdaBound": AdaBound(alpha=5e-2),
# "AMSBound": AMSBound(alpha=5e-2),
}
current_x = np.full(len(opt_dict), start_x, dtype=float)
current_y = np.full(len(opt_dict), start_y, dtype=float)
cmap = plt.get_cmap("rainbow")
coloring = [cmap(i) for i in np.linspace(0, 1, len(opt_dict))]
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.plot_surface(X, Y, Z, cmap="autumn", alpha=0.8)
ax.contour(X, Y, Z, cmap="autumn", levels=elevation, alpha=0.8)
ax.set_xlim(x[0], x[-1])
ax.set_ylim(y[0], y[-1])
ax.set_zlim(np.min(Z), np.max(Z))
ax.set_position([0.1, 0.1, 0.6, 0.8])
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
ax.grid()
ax.view_init(60)
paths = np.zeros((epoch + 1, len(opt_dict), 3))
for j in range(len(opt_dict)):
paths[0, j, 0] = current_x[j]
paths[0, j, 1] = current_y[j]
paths[0, j, 2] = g(current_x[j], current_y[j])
for i in range(1, epoch+1):
for j, opt in enumerate(opt_dict):
dx, dy = opt_dict[opt].update(dgx(current_x[j], current_y[j]),
dgy(current_x[j], current_y[j]),
t=i,
w=current_x[j], b=current_y[j],
dfw=dgx, dfb=dgy,
f=g(current_x[j], current_y[j]))
current_x[j] += dx
current_y[j] += dy
paths[i, j, 0] = current_x[j]
paths[i, j, 1] = current_y[j]
paths[i, j, 2] = g(current_x[j], current_y[j])
class TrajectoryAnimation3D(animation.FuncAnimation):
def __init__(self, paths, labels=[], fig=None, ax=None, frames=None,
interval=60, repeat_delay=5, blit=True, coloring=None,
**kwargs):
if fig is None:
if ax is None:
fig, ax = plt.subplots()
else:
fig = ax.get_figure()
else:
if ax is None:
ax = fig.gca()
self.fig = fig
self.ax = ax
self.paths = paths
if frames is None:
frames = paths.shape[0]
self.lines = []
self.points = []
for j, opt in enumerate(labels):
line, = ax.plot([], [], [], label=opt, lw=2, color=coloring[j])
point, = ax.plot([], [], [], marker="o", color=coloring[j])
self.lines.append(line)
self.points.append(point)
super().__init__(fig, self.animate, init_func=self.init_anim,
frames=frames, interval=interval, blit=blit,
repeat_delay=repeat_delay, **kwargs)
def init_anim(self):
for line, point in zip(self.lines, self.points):
line.set_data([], [])
line.set_3d_properties([])
point.set_data([], [])
point.set_3d_properties([])
return self.lines + self.points
def animate(self, i):
j = int(0)
for line, point in zip(self.lines, self.points):
line.set_data(self.paths[:i, j, 0], self.paths[:i, j, 1])
line.set_3d_properties(self.paths[:i, j, 2])
point.set_data(self.paths[i, j, 0], self.paths[i, j, 1])
point.set_3d_properties(self.paths[i, j, 2])
j += 1
return self.lines + self.points
anim = TrajectoryAnimation3D(paths, labels=opt_dict, fig=fig, ax=ax,
coloring=coloring)
fig.legend(bbox_to_anchor=(0.96, 0.9))
fig.suptitle("Optimizer comparison")
plt.show()
test.py
#%matplotlib nbagg #Für Jupiter
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from mpl_toolkits.mplot3d import Axes3D
from optimizers import * #Kommentar zu jupyter
#Es wird davon ausgegangen, dass sich das Optimierungsmodul im selben Ordner befindet.
def g(x, y):
#return (x**2 - y**2) * 1
#return np.tanh(x)**2 + np.tanh(y)**2
return -(np.sinc(x) + np.sinc(y)) + (x**2 + y**2)/7
def dgx(x, y):
#return 2*x * 1
#return 2 * np.tanh(x) / np.cosh(x)**2
return np.sin(np.pi*x)/(np.pi * x**2) + 2*x/7 - np.cos(np.pi*x)/x
def dgy(x, y):
#return -2*y * 1
#return 2 * np.tanh(y) / np.cosh(y)**2
return np.sin(np.pi*y)/(np.pi * y**2) + 2*y/7 - np.cos(np.pi*y)/y
num = 401
#x = np.linspace(-2, 2, num)
#y = np.linspace(-2, 2, num)
x = np.linspace(-5, 5, num)
y = np.linspace(-5, 5, num)
X, Y = np.meshgrid(x, y)
Z = g(X, Y)
elevation = np.arange(np.min(Z), np.max(Z), 0.25)
#start_x = -1.5
#start_y = -1e-4
#start_x = -1
#start_y = 2
start_x = -3
start_y = 4
exact_x = 0
exact_y = 0
epoch = 500
N = epoch
seed=2
np.random.seed(seed=seed)
#fig = plt.figure()
#ax = fig.add_subplot(111, projection="3d")
#ax.set_zlim(-1, 1)
#im = ax.plot_surface(X, Y, Z, cmap="autumn")
#fig.show()
opt_dict = {
# "SDG": SGD(eta=5e-2),
# "MSGD": MSGD(eta=5e-2),
# "NAG": NAG(eta=5e-2),
# "AdaGrad": AdaGrad(eta=1e-1),
# "RMSprop": RMSprop(eta=5e-2),
# "AdaDelta": AdaDelta(),
# "Adam": Adam(alpha=5e-2),
# "RMSpropGraves": RMSpropGraves(eta=1e-2),
# "SMORMS3": SMORMS3(eta=1e-2),
# "AdaMax": AdaMax(alpha=2e-2),
# "Nadam": Nadam(alpha=2e-2),
# "Eve": Eve(alpha=5e-2),
"SantaE": SantaE(eta=1e-3, burnin=10, N=N),
"SantaSSS": SantaSSS(eta=1e-3, burnin=10, N=N),
# "AMSGrad": AMSGrad(alpha=5e-2),
# "AdaBound": AdaBound(alpha=5e-2),
# "AMSBound": AMSBound(alpha=5e-2),
}
current_x = np.full(len(opt_dict), start_x, dtype=float)
current_y = np.full(len(opt_dict), start_y, dtype=float)
cmap = plt.get_cmap("rainbow")
coloring = [cmap(i) for i in np.linspace(0, 1, len(opt_dict))]
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
ax.plot_surface(X, Y, Z, cmap="autumn", alpha=0.8)
ax.contour(X, Y, Z, cmap="autumn", levels=elevation, alpha=0.8)
ax.set_xlim(x[0], x[-1])
ax.set_ylim(y[0], y[-1])
ax.set_zlim(np.min(Z), np.max(Z))
ax.set_position([0.1, 0.1, 0.6, 0.8])
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
ax.grid()
ax.view_init(60)
paths = np.zeros((epoch + 1, len(opt_dict), 3))
for j in range(len(opt_dict)):
paths[0, j, 0] = current_x[j]
paths[0, j, 1] = current_y[j]
paths[0, j, 2] = g(current_x[j], current_y[j])
for i in range(1, epoch+1):
for j, opt in enumerate(opt_dict):
dx, dy = opt_dict[opt].update(dgx(current_x[j], current_y[j]),
dgy(current_x[j], current_y[j]),
t=i,
w=current_x[j], b=current_y[j],
dfw=dgx, dfb=dgy,
f=g(current_x[j], current_y[j]))
current_x[j] += dx
current_y[j] += dy
paths[i, j, 0] = current_x[j]
paths[i, j, 1] = current_y[j]
paths[i, j, 2] = g(current_x[j], current_y[j])
class TrajectoryAnimation3D(animation.FuncAnimation):
def __init__(self, paths, labels=[], fig=None, ax=None, frames=None,
interval=60, repeat_delay=5, blit=True, coloring=None,
**kwargs):
if fig is None:
if ax is None:
fig, ax = plt.subplots()
else:
fig = ax.get_figure()
else:
if ax is None:
ax = fig.gca()
self.fig = fig
self.ax = ax
self.paths = paths
if frames is None:
frames = paths.shape[0]
self.lines = []
self.points = []
for j, opt in enumerate(labels):
line, = ax.plot([], [], [], label=opt, lw=2, color=coloring[j])
point, = ax.plot([], [], [], marker="o", color=coloring[j])
self.lines.append(line)
self.points.append(point)
super().__init__(fig, self.animate, init_func=self.init_anim,
frames=frames, interval=interval, blit=blit,
repeat_delay=repeat_delay, **kwargs)
def init_anim(self):
for line, point in zip(self.lines, self.points):
line.set_data([], [])
line.set_3d_properties([])
point.set_data([], [])
point.set_3d_properties([])
return self.lines + self.points
def animate(self, i):
j = int(0)
for line, point in zip(self.lines, self.points):
line.set_data(self.paths[:i, j, 0], self.paths[:i, j, 1])
line.set_3d_properties(self.paths[:i, j, 2])
point.set_data(self.paths[i, j, 0], self.paths[i, j, 1])
point.set_3d_properties(self.paths[i, j, 2])
j += 1
return self.lines + self.points
anim = TrajectoryAnimation3D(paths, labels=opt_dict, fig=fig, ax=ax,
coloring=coloring)
fig.legend(bbox_to_anchor=(0.96, 0.9))
fig.suptitle("Optimizer comparison")
plt.show()
Referenz
- 3D-Plot mit Matplotlib
- Versuchen Sie, eine feste (3D) topografische Karte mit der Animationsfunktion von matplotlib zu drehen
- Visualizing and Animating Optimization Algorithms with Matplotlib
Deep Learning-Serie
- Einführung in Deep Learning ~ Grundlagen ~
- Einführung in Deep Learning ~ Codierungsvorbereitung ~
- Einführung in Deep Learning ~ Forward Propagation ~
- Einführung in Deep Learning ~ Backpropagation ~
- Liste der Aktivierungsfunktionen (2020)
- Liste der Gradientenabstiegsmethoden (2020)
- Sehen und verstehen! Vergleich der Optimierungsmethoden (2020)
- Im2col gründliches Verständnis
- Vollständiges Verständnis der Funktion numpy.pad
Recommended Posts