[PYTHON] [Mathematik] Wenn Sie die Bedeutung von "innerem Produkt" grafisch verstehen, können Sie verschiedene Dinge sehen.
Wenn Sie anfangen, lineare Algebra zu studieren, kommt sie ziemlich schnell heraus, nicht wahr? Die Berechnung selbst ist nicht so schwierig, aber ich denke, es gibt Leute, die es nicht richtig machen. Ich auch, ich war so. In dieser Visualisierungsserie werde ich mich also auf das "innere Produkt" konzentrieren.
Auch in der Statistik gibt es Dinge, die vom inneren Produkt überall verstanden werden können, und es wird zum "inneren Produkt": grinsen :. Vektoren sind eine Folge von Daten, daher sind sie für die Statistik sehr relevant. Es wird ab dem nächsten Mal in der Statistik behandelt, aber zuerst vom inneren Produkt.
0. Eine kleine Schlussfolgerung zuerst
Da die vorherige Theorie notwendig ist, möchte ich zuerst nur die Schlussfolgerung der Bedeutung des inneren Produkts schreiben. Das innere Produkt kann wie folgt als mathematische Formel geschrieben werden.
{\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ \cos\theta
Um es visuell auszudrücken, wird es wie folgt und es kann die Bedeutung der Länge des Vektors $ {\ bf a} $ multipliziert mit der Länge des Vektors $ {\ bf c} $ gegeben werden. Ich werde. ($ {\ bf c} $ ist eine Projektion des Vektors $ {\ bf b} $ über den Vektor $ {\ bf a} $.)

Wenn Sie bisher "Ja, das stimmt" sagen, warten Sie bitte eine Weile, da ich beim nächsten Mal erklären werde, wie das innere Produkt in der Statistik gut gehandhabt wird. (Da die Folienversion bereits erklärt wurde, lesen Sie bitte ** hier ** bis dahin)
Wenn Sie wissen möchten, "warum Sie das sagen können" und "was das ist", möchte ich es von nun an erklären. Fahren Sie also bitte so fort, wie es ist.
1. Definition und Berechnung des inneren Produkts
Beginnen wir mit der mathematischen Definition. Wenn es einen Vektor $ {\ bf a} = (a_1, \ cdots, a_n), {\ bf b} = (b_1, \ cdots, b_n) $ gibt, wird das innere Produkt wie folgt definiert.
{\bf a} \cdot {\bf b} = a_1b_1+\cdots+a_nb_n = \sum_{i=1}^n a_ib_i
Es bedeutet, die entsprechenden Elemente jedes Vektorelements zu multiplizieren (das erste Element $ a_1 $ und das erste Element $ b_1 $ entsprechen usw.) und sie alle zu addieren. Betrachten wir die visuelle Bedeutung davon.
2. Anwendung des Kosinussatzes
Um das innere Produkt zu verstehen, verwenden wir den Kosinussatz. Die Formel ist unten.
\|{\bf b}-{\bf a}\|^2 = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ \cos\theta \cdots (*)

Die Beziehung zwischen den Längen jeder Seite des Dreiecks, wie oben beschrieben, erfüllt diese Formelbeziehung.
Auch das Quadrat der Länge von $ {\ bf a} $
\|{\bf a}\|^2 = \left(\sqrt{a_1\cdot a_1 + \cdots + a_n\cdot a_n}\right)^2 =a_1\cdot a_1 + \cdots + a_n\cdot a_n\\
=\sum_{i=1}^n x_i^2 = {\bf a} \cdot {\bf a}
Kann durch das innere Produkt desselben Vektors dargestellt werden.
Dies
\|{\bf b}-{\bf a}\|^2 = ({\bf b}-{\bf a})\cdot({\bf b}-{\bf a}) = {\bf a}\cdot{\bf a} + {\bf b}\cdot{\bf b} - 2 {\bf a}\cdot{\bf b} \\
= \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2 {\bf a}\cdot{\bf b}
Einsetzen in die (*) Gleichung des Kosinussatzes,
\|{\bf b}-{\bf a}\|^2 = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta\\
\Rightarrow \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2 {\bf a}\cdot{\bf b} = \|{\bf a}\|^2 + \|{\bf b}\|^2 - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta\\
Auf beiden Seiten
- 2 {\bf a}\cdot{\bf b} = - 2\|{\bf a}\|\|{\bf b}\|\ cos\theta \\
\Rightarrow {\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ cos\theta
Das innere Produkt ist also
\|{\bf a}\|\|{\bf b}\|\ \cos \theta
Es stellte sich heraus.
Wow, ich verstehe ...? ?? ??
Na und? Ich fühle mich···
Aber diese Form ist sehr wichtig, bitte denken Sie daran.
Dann das
3.||a|| ||b||Entdecken Sie das Geheimnis von cosθ#
3.1 Bestätigung von cos θ und das Konzept der Projektion
Zunächst möchte ich $ \ cos \ theta $ noch einmal bestätigen. Die mathematische Definition lautet
\cos \theta = \frac{\|c\|}{\|r\|}
ist. In der Grafik dargestellt

$ r $ ist der Radius und $ x $ ist der Vektor vom Vektor $ r $ zu diesem Punkt, der eine Linie senkrecht zur x-Achse zeichnet. Als Bild, wie unten gezeigt, ist es der Teil, der das Licht von direkt oben beleuchtet und zu einem Schatten wird. (Es heißt Projektion.) ** Der durch Beleuchten des Daches $ {\ bf r} $ erzeugte Schattenteil ist der Vektor $ {\ bf c} $. ** **.

3.2 Bedeutung des inneren Produkts
\|c\| = \|r\|\cos \theta
Die Länge von c ist also
Hier waren übrigens die Hausaufgaben des vorherigen Abschnitts
\|{\bf a}\|\|{\bf b}\|\ \cos \theta
Kommen wir zurück zu. Versuchen Sie in ähnlicher Weise, ein Licht von oben zu scheinen.

Vektor
{\bf a}\cdot{\bf b} = \|{\bf a}\|\|{\bf b}\|\ \cos\theta
Also, ** "Länge des Vektors $ {\ bf a} $" ** und ** "Länge des Vektors $ {\ bf b} $ projiziert auf den Vektor $ {\ bf a} $" Es gilt als Produkt von **.
Da das innere Produkt auch ** "Produkt" ** ist, handelt es sich um eine Art Multiplikation, aber ich denke, dass das Bild der ** Multiplikation zwischen Vektoren das Bild der Übereinstimmung der Richtungen und der Multiplikation der Länge ** sein sollte. Ich bin.
3.3 Wenn die Richtungen der beiden Vektoren vertikal sind
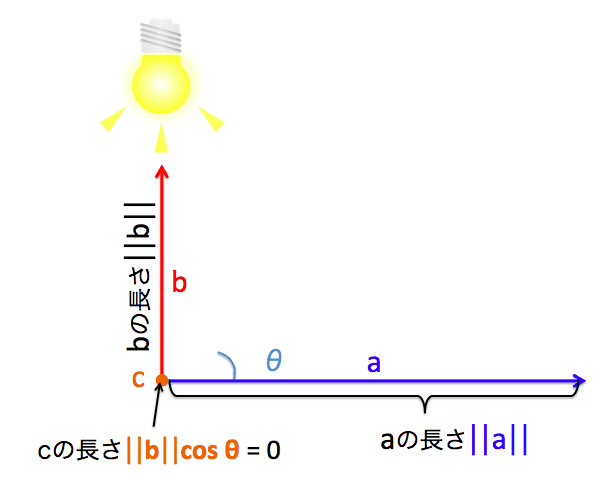
Wenn der Winkel zwischen den beiden Vektoren richtig ist, können Sie keinen Schatten werfen, selbst wenn Sie ein Licht von oben scheinen. Daher wird zu diesem Zeitpunkt die Länge des Vektors $ {\ bf c} $ 0. Mit anderen Worten, wenn der Winkel richtig ist, ist das innere Produkt ebenfalls 0.
3.3 Für einen Vektor der Länge 1
Mach die Geschichte einfacher
\cos \theta = \frac{\|c\|}{\|r\|} = \|c\|
Daher wird die Länge von $ {\ bf c} $ so wie sie ist zum Wert von $ \ cos \ theta $.
 Wenn Sie sich nun das innere Produkt von $ {\ bf x} $ und $ {\ bf r} $ ansehen,
Wenn Sie sich nun das innere Produkt von $ {\ bf x} $ und $ {\ bf r} $ ansehen,
{\bf x}\cdot{\bf r} = \|{\bf x}\|\|{\bf r}\|\ \cos\theta = 1 \cdot 1 \cdot \cos\theta = \cos\theta
Daher ist das innere Produkt zweier Vektoren mit einer Länge von 1 $ \ cos \ theta $ **: smile:
Im nächsten Artikel werde ich über "Szenen schreiben, in denen interne Produkte in Statistiken verwendet werden". Ich werde anhand von Grafiken und Animationen in Python erklären, wie die Varianz / Standardabweichung, der Kovarianz- / Korrelationskoeffizient, der Regressionskoeffizient usw. in Bezug auf dieses innere Produkt aussehen.
Recommended Posts