[PYTHON] Ich habe versucht, die Anzeigenoptimierung mithilfe des Banditenalgorithmus zu simulieren
Einführung
Der Zweck dieses Eintrags besteht darin, die Eigenschaften jeder Methode des Banditenalgorithmus zu verstehen, indem Simulationen unter Annahme tatsächlicher Anwendungsfälle durchgeführt werden.
Der folgende Qiita-Beitrag wird häufig auf Japanisch über den Banditenalgorithmus erwähnt. http://qiita.com/yuku_t/items/6844aac6008911401b19
In den folgenden Materialien werden auch die Details und Merkmale der einzelnen Methoden sowie einfache Simulationen vorgestellt. http://www.slideshare.net/greenmidori83/ss-28443892
Da die Einführung der Methode in das obige Material sehr einfach zu verstehen ist, werden wir die Methode in diesem Eintrag nicht vorstellen.
Angenommener Anwendungsfall
Sie schalten derzeit eine Anzeige, die 10.000 Mal geschaltet wurde und eine Klickrate von 1,2% für 60 Yen pro Klick aufweist. Ich habe mich entschlossen, verschiedene Muster von Bannern auszuprobieren, um mehr angeklickte Anzeigen zu finden. Ich habe 10 neue Banner gemacht. Angenommen, zwei dieser Banner haben eine bessere Klickrate als das aktuelle, drei entsprechen der aktuellen Anzeige und die restlichen fünf haben eine niedrigere Klickrate als das aktuelle.
-1,3% 2 Stück -1,2% ist 3 -1,1% ist 3
- Zwei 1,0%
Warum Sie die Klickrate erhöhen möchten
Es hat nichts mit dem Hauptthema zu tun, aber warum möchten Sie die Klickrate erhöhen und warum ist es sinnvoll, ein Experiment durchzuführen, obwohl die Klickrate nur um 0,1% steigt? Lassen Sie uns darüber nachdenken. Sie könnten denken, dass eine Erhöhung der Klickrate nicht viel Sinn macht, da sich der Geldbetrag, den Sie für jeden Klick bezahlen, nicht ändert. Aus Sicht des Werbetreibenden verringert das Platzieren einer Anzeige mit einer niedrigen Klickrate jedoch den Umsatz. Wenn die Klickrate niedrig ist, ist es daher schwierig, die Anzeige anzuzeigen. Zu diesem Zeitpunkt wird häufig ein Index namens eCPM verwendet. eCPM ist ein Index dafür, wie viel Umsatz durch 1000-maliges Anzeigen der Anzeige erzielt werden kann. Klickrate * 1000 * Berechnet anhand der Kosten pro Klick. Da Anzeigen mit hohem EPCM eher geschaltet werden, können viele Nutzer durch Erhöhen der Klickrate zu den gleichen Kosten pro Klick auf ihre Zielseite geleitet werden. In diesem Fall beträgt die Klickrate beispielsweise 1,2% und die Kosten pro Klick 60 Yen, sodass der eCPM 720 Yen beträgt. Wenn sich die Klickrate um 0,1% erhöht, beträgt der eCPM 780 Yen. Selbst wenn die Kosten pro Klick 56 Yen betragen, beträgt der eCPM zu diesem Zeitpunkt 726 Yen. Wenn sich die Klickrate um 0,1% erhöht, kann der Stückpreis für das Erhalten der gleichen Anleitung für die Zielseite um 4 Yen gesenkt werden. Wenn beispielsweise ein Produkt auf dieser Zielseite zu 1% gekauft wird, werden die Kosten für den Verkauf eines Produkts um 400 Yen reduziert. Von Fall zu Fall ist die Erhöhung der Klickraten auf diese Weise ein sehr wichtiger Faktor für den Verkauf von Dingen über Webwerbung.
Simulation
Die Implementierung wurde aus dem Folgenden entlehnt
https://github.com/johnmyleswhite/BanditsBook
Werfen wir einen Blick auf Epsilon Greedy, Softmax, UCB
Epsilon Greedy
Epsilon Greedy ist eine Methode zur Auswahl einer Option, die Sie derzeit mit einer gewissen Wahrscheinlichkeit nicht für die beste halten. Zunächst werde ich versuchen, bei etwa 10% zu suchen. Versuchen wir es 1000 Mal.
execfile("core.py")
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
algo1 = EpsilonGreedy(0.1, counts, values)
for t in range(1000):
chosen_arm = algo1.select_arm()
reward = arms[chosen_arm].draw()
algo1.update(chosen_arm, reward)
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl von Versuchen | 77 | 109 | 82 | 38 | 38 | 50 | 264 | 205 | 49 | 47 | 41 |
| Bewertungswahrscheinlichkeit | 1.2% | 0.9% | 3.7% | 0% | 0% | 2.0% | 2.3% | 2.0% | 0% | 0% | 0% |
Mit 11 Auswahlmöglichkeiten können Sie in etwa 1.000 Versuchen überhaupt nichts sagen. Dieses Ergebnis variiert von Zeit zu Zeit stark, da es auch von der Erzeugung von Zufallszahlen abhängt.
Was ist, wenn Sie es 10.000 Mal versuchen?
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl von Versuchen | 1,321 | 824 | 481 | 623 | 1,827 | 562 | 1,026 | 968 | 452 | 1206 | 710 |
| Bewertungswahrscheinlichkeit | 1.2% | 1.2% | 0.6% | 1.2% | 1.3% | 0.7% | 1.2% | 1.1% | 0.9% | 1.2% | 1.3% |
Es ist kein schreckliches Ergebnis, aber es ist schwer zu sagen, dass es ein gutes Ergebnis ist.
Versuchen Sie als Nächstes, den Suchgrad auf etwa 50% zu erhöhen. Erste 1000 mal
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl von Versuchen | 239 | 70 | 40 | 72 | 37 | 44 | 137 | 45 | 52 | 211 | 53 |
| Bewertungswahrscheinlichkeit | 1.2% | 1.4% | 0% | 1.4% | 0% | 0% | 1.5% | 0% | 0% | 1.9% | 0% |
Ist es ein Zustand, in dem Epsilon gleichmäßig durchsucht wird, verglichen mit 10%? Nächste 10.000 Mal
| base | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Anzahl von Versuchen | 1,035 | 1,915 | 8,120 | 1,046 | 1,026 | 1,104 | 885 | 899 | 1,007 | 1,354 | 1,609 |
| Bewertungswahrscheinlichkeit | 1.2% | 1.3% | 1.3% | 1.1% | 1.1% | 1.0% | 0.9% | 1.1% | 1.1% | 0.7% | 1.2% |
Ich konnte das beste Banner finden, aber es ist einfach passiert. Es ist zu sehen, dass andere Banner im Vergleich zu 10% gleichmäßig ausprobiert werden. Da es von Versuch zu Versuch große Unterschiede gibt, lassen Sie uns den Durchschnitt der mehrmals wiederholten epcm bewerten.
eCPM fragt nach
def calc_ecpm(algo):
total = sum(algo.counts) - 10000
ecpm = 0.0
for idx, count in enumerate(algo.counts):
if idx == 0:
count -= 10000
if count == 0:
continue
ecpm += 1000 * 60 * algo.values[idx] * float(count)/total
return ecpm
Wenn dann die Parameter in 0,1-Schritten von 0,1 bis 0,9 eingestellt werden und der Bandit von 10.000 Versuchen 1.000 Mal für jeden Parameter ausgeführt wird, sieht die ecpm so aus.
def run_eg(ep, counts, values, arms):
algo = EpsilonGreedy(ep, counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_ecpm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for ep in xrange(1, 10):
print ep * 0.1
for _ in xrange(10000):
data.append((ep*0.1, run_eg(ep*0.1, counts, values, arms)))
return pandas.DataFrame(data, columns=['ep', 'epcm'])
result = run()
result.boxplot(by="ep")

Wenn das Epsilon klein ist, variiert es stark. Es scheint jedoch, dass das Ergebnis umso kleiner ist, je größer das Ergebnis ist. Es wurde auch festgestellt, dass es im Wesentlichen die ursprüngliche ecpm von 720 überschreitet. Es scheint, dass selbst ein so einfacher Algorithmus ausreichend nützliche Ergebnisse liefern kann.
SoftMax
Der Parameter von Softmax ist tau. Je kleiner es ist, desto mehr vertrauen Sie dem bereits berechneten Wert. Dadurch werden die Parameter von 2 ^ -5 bis 2 ^ 5 jeweils 1000 Mal ausprobiert.
def run_sm(tau, counts, values, arms):
algo = Softmax(tau, counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_epcm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for i in xrange(10):
tau = 2**(i - 5)
print tau
for _ in xrange(10000):
data.append((tau, run_sm(tau, counts, values, arms)))
return pandas.DataFrame(data, columns=['tau', 'epcm'])
result = run()
result.boxplot(by="tau")

Ich habe schlechtere Ergebnisse erzielt als normalerweise! Dies liegt daran, dass softmax immer wieder mit einer bestimmten Wahrscheinlichkeit schlechte Werte zieht. Bei der Verwendung von Softmax scheint es notwendig zu sein, schlechte Optionen schnell auszuschalten.
UCB
Endlich UCB UCB hat keine Parameter, also werde ich es so machen, wie es ist
def run_ucb(counts, values, arms):
algo = UCB1(counts, values)
for t in xrange(10000):
chosen_arm = algo.select_arm()
reward = arms[chosen_arm].draw()
algo.update(chosen_arm, reward)
return calc_epcm(algo)
def run():
data = []
arm_rates = [0.012, 0.013, 0.013, 0.012, 0.012, 0.012, 0.011, 0.011, 0.011, 0.01, 0.01]
arms = [BernoulliArm(r) for r in arm_rates]
counts = [10000, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
values = [0.012, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
for _ in xrange(10000):
data.append(run_ucb(counts, values, arms))
return pandas.DataFrame(data, columns=['epcm'])
result = run()
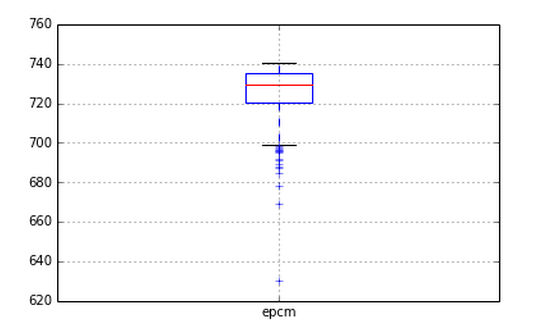
Es ist ersichtlich, dass die Suche durchgeführt werden kann, ohne den epcm zu senken. Es wird niedriger sein als Epsilon Greedy, aber dieser Bereich wird wahrscheinlich ein Kompromiss mit der Suchgeschwindigkeit sein.
Vergleich und Berücksichtigung jeder Methode
Ich möchte es später schreiben. Ich möchte es auch mit dem A / B-Test vergleichen.
Zusammenfassung
Ich kann nicht sagen, welche Methode in diesem Eintrag besser ist. Ich denke, es gibt eine Menge Dinge, über die wir nachdenken müssen, wenn wir mehr Anwendungsfälle verfolgen wollen. Ich hoffe, es wird dazu führen, dass man irgendwie versteht, was der Banditenalgorithmus ist.
Der Banditenalgorithmus zeichnet sich dadurch aus, dass er unter Verwendung der bisher erhaltenen Datenbestände suchen kann. Ich denke, einer der Vorteile ist, dass Exploration das Risiko einer Gefährdung des Geschäfts verringern kann, indem wichtige Indikatoren wie eCPM gesenkt werden. Daher wollte ich im Voraus überprüfen, welche Art von Dienstprogramm erhalten werden kann, wenn Datenbestände vorhanden sind, anstatt die richtige Wahl zu treffen. Deshalb habe ich diese Art der Simulation ausprobiert. Wir hoffen, Sie finden es hilfreich. Und wenn Sie eine Meinung haben, können Sie diese gerne kommentieren!
Recommended Posts