Verwendung der OpenGoddard 3-Python-Bibliothek zur nichtlinearen optimalen Steuerung und Trajektoriengenerierung

https://github.com/istellartech/OpenGoddard https://istellartech.github.io/OpenGoddard/

Verwendung von OpenGoddard 1 Verwendung von OpenGoddard 2 OpenGoddard How to use 3 ← Jetzt hier Öffnen Sie Goddard How to use 4

Optimaler Raketenanstieg (1. Stufe)

Als Kombinationstechnik aus Normalisierung (Skalierung) und Knotenmethode, die wir bisher ausprobiert haben, führen wir eine Schubsteuerungsoptimierung mit einem Wert durch, der dem einer tatsächlichen Rakete nahe kommt.

Als Referenzproblem wird auf das im folgenden Dokument beschriebene Problem des optimalen Raketenanstiegs verwiesen. Dies verwendet auch die gleiche Legendre-Gauss-Lobatto-Pseudospektrum-Methode wie Open Goddard.

Rea, Jeremy Ryan. A legendre pseudospectral method for rapid optimization of launch vehicle trajectories. Diss. Massachusetts Institute of Technology, 2001. http://hdl.handle.net/1721.1/8608

Die kinetische Gleichung ist fast dieselbe wie Verwendung 2. Ändern Sie nur den Wert. Vergessen Sie nicht zu normalisieren, da zum Ändern des Werts eine Zahl für die Normalisierung erforderlich ist.

Danach schreibe es gut SOLVE!

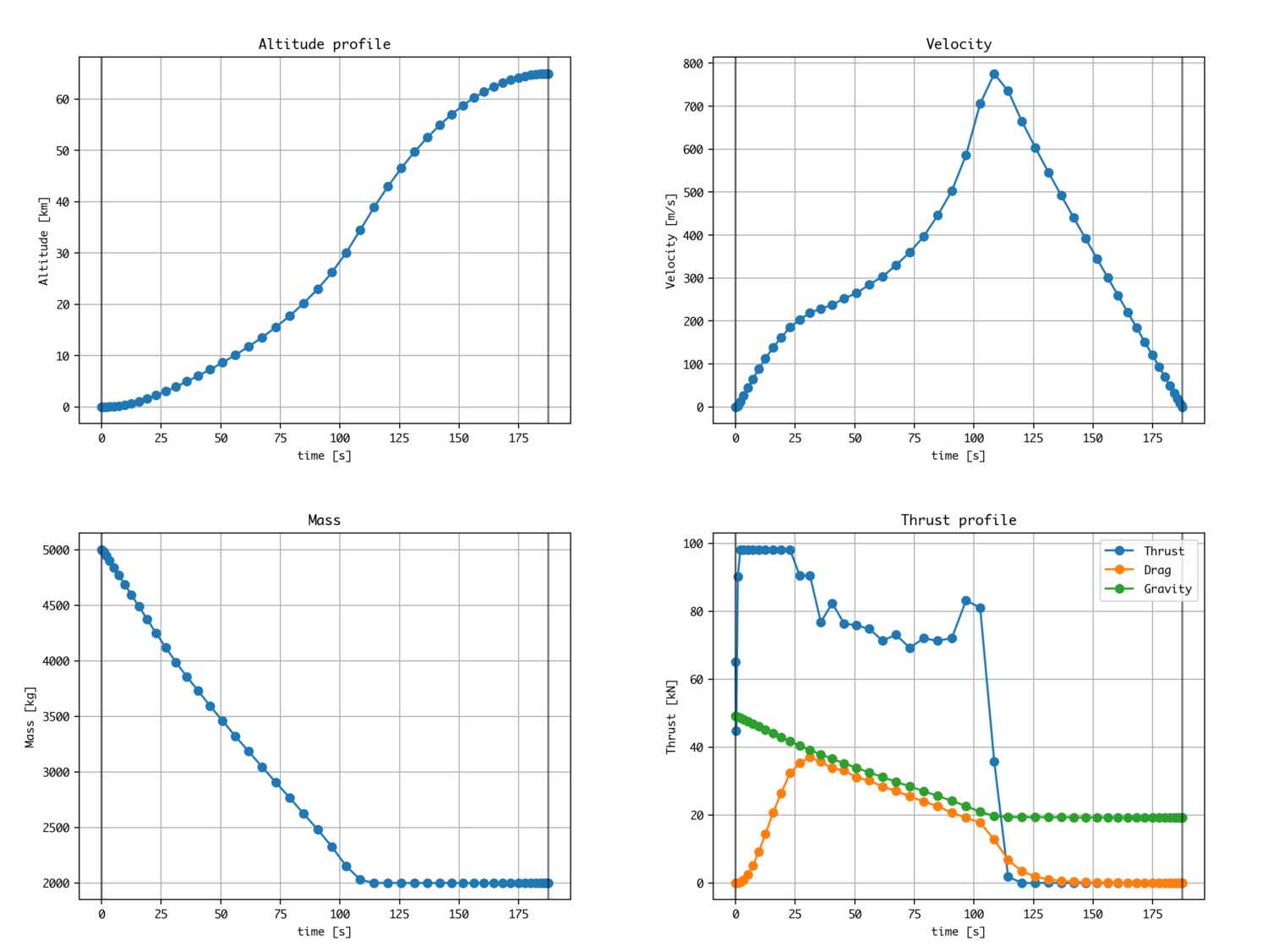
Die Grafik ähnelt dem Papier. (Je nachdem, wie der Konvergenzwert eingestellt ist, unterscheidet er sich geringfügig.)

Optimaler Raketenanstieg (2 Stufen)

Die Schubsteuerungsoptimierung der zweistufigen Rakete erfolgt nach der Knotenmethode. Die wichtigsten Änderungen sind wie folgt. Die Standardlösung (Guess-Teil) wurde ebenfalls ein wenig geändert.

time_init = [0.0, 300, 600]
n = [25, 25]
num_states = [3, 3]
num_controls = [1, 1]
max_iteration = 30
prob = Problem(time_init, n, num_states, num_controls, max_iteration)

prob.dynamics = [dynamics, dynamics]
prob.knot_states_smooth = [False]

Die Zustandsvariable (Masse hier) ist als diskontinuierlich definiert. Fügen Sie der Einschränkungsbedingung (Gleichheit) Folgendes hinzu:

# knotting condition
R1 = prob.states(0, 0)
v1 = prob.states(1, 0)
m1 = prob.states(2, 0)
R2 = prob.states(0, 1)
v2 = prob.states(1, 1)
m2 = prob.states(2, 1)
result.add(R1[-1] - R2[0])
result.add(v1[-1] - v2[0])
result.add(m1[-1] - m2[0] - 1200)

Wenn Sie eingeben, sind Höhe und Geschwindigkeit kontinuierlich, und Sie können den Massenverlust (diskontinuierlich) zum Zeitpunkt der Trennung definieren.

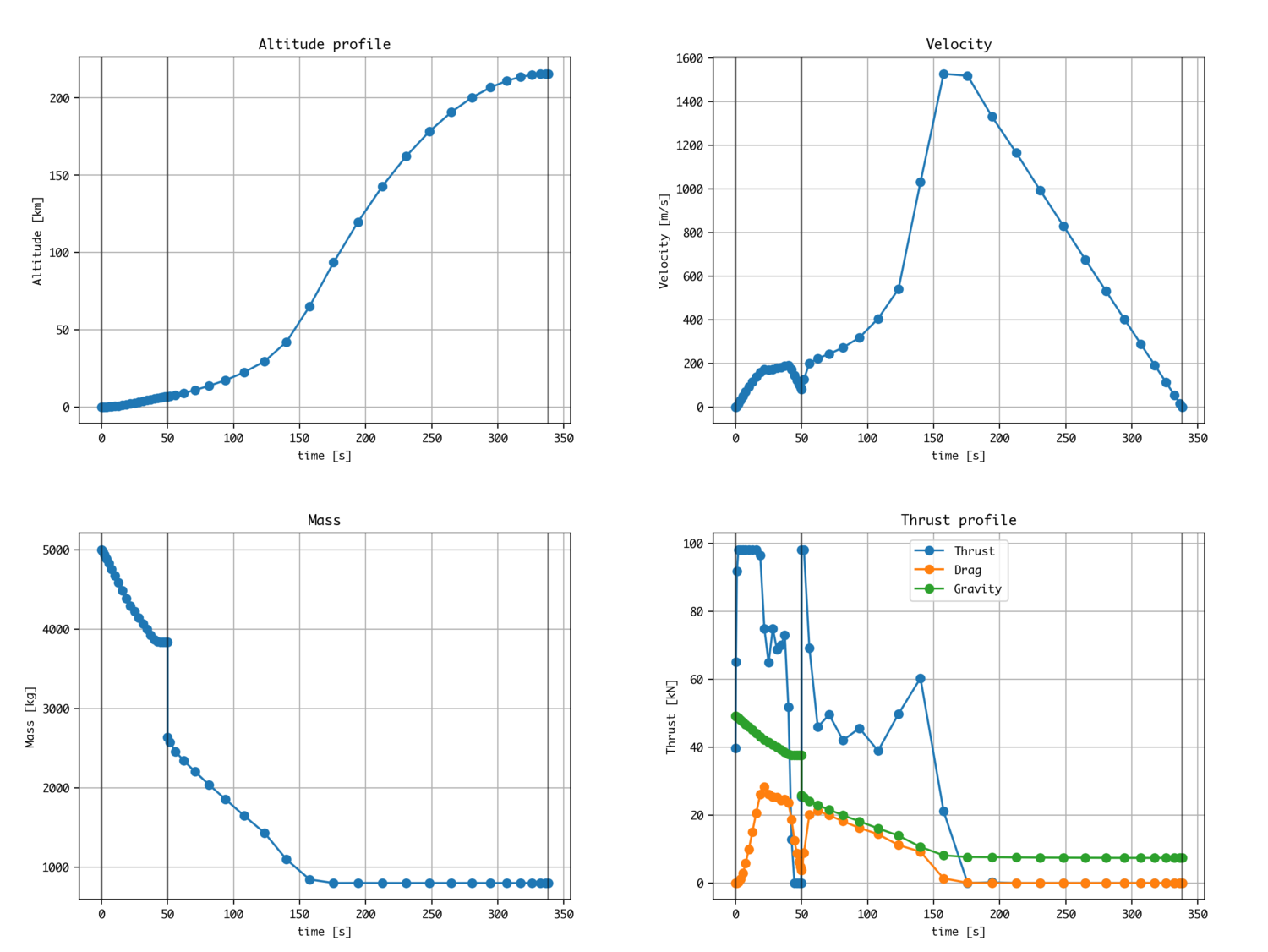
Zweistufige Rakete in zweidimensionalen Koordinaten

Das Beispiel von OpenGoddard enthält ein Beispiel unter der Annahme, dass die Rakete in zwei Dimensionen in die erdnahe Umlaufbahn gebracht wird (Polarkoordinatensystem).

Das Ergebnis von Open Goddard ist, dass es am besten ist, die obere Rakete in der Mitte anzuhalten und erneut zu entzünden, um sie in die Umlaufbahn zu bringen. Weltraumingenieure auf der ganzen Welt entwickeln Raketen usw. basierend auf den Ergebnissen dieser optimalen Umlaufbahnen.

Apropos

Die Methode, die nicht wieder entzündet wird, wird als Direktverbrennungsmethode bezeichnet, aber das erforderliche technische Niveau ist für die Direktverbrennung niedriger, und in der Realität kann die Direktverbrennung aufgrund der Kommunikation mit dem Boden oder aufgrund technischer Probleme angewendet werden. In der Realität ist es erforderlich, eine Flugbahn mit verschiedenen Rückhaltebedingungen zu erstellen.