OpenGoddard Verwendung der 2-Python-Bibliothek zur nichtlinearen optimalen Steuerung und Trajektoriengenerierung

https://github.com/istellartech/OpenGoddard https://istellartech.github.io/OpenGoddard/

Verwendung von OpenGoddard 1 Open Goddard How to use 2 ← Jetzt hier Verwendung von OpenGoddard 3 Verwendung von OpenGoddard 4

Goddard-Problem (Problem der optimalen Raketenaufstiegskontrolle in der Atmosphäre)

Wir werden das Goddard-Problem lösen, das ein klassisches Problem in der Raketentechnik ist, das Problem der optimalen Schubkontrolle für den optimalen Aufstieg einer Rakete in die Atmosphäre. Weitere Informationen finden Sie in der Datei Beispiel.

Bewegungsgleichung

Betrachten Sie die Bewegung der Rakete in einer Dimension (nur Höhe). Berücksichtigen Sie die Maximierung der Höhe, indem Sie den Schub und den Luftwiderstand des Raketentriebwerks berücksichtigen. T: Schub D: Widerstand (Luftwiderstand) g: Schwerkraftbeschleunigung

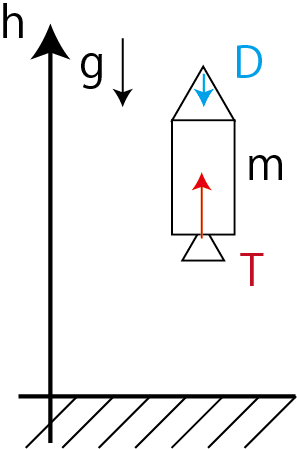
\begin{align}
\dot{h} &= v \\
\dot{v} &= \frac{T - D}{m} - g \\
\dot{m} &= - \frac{T}{c}
\end{align}

Rückhaltebedingung

Geben Sie die oberen und unteren Grenzen der Anfangsbedingung, der Endwertbedingung, der Zustandsvariablen und der Steuervariablen ein.

Bewertungsfunktion

Geben Sie den Wert ein, den Sie minimieren möchten. Hier möchten wir die Höhe maximieren, achten Sie also wie folgt auf das Zeichen.

J = -h

Ergebnis

Das Ergebnis war, dass es besser war, zuerst Vollgas zu geben und dann den Schub in der Mitte zu reduzieren. Dies ist ein Kompromiss zwischen der Eigenschaft, dass der Schub so groß wie möglich sein sollte, um die Verzögerung aufgrund der Schwerkraft in Bezug auf das Phänomen zu verringern, und der Eigenschaft, dass es besser ist, in einer dichten Luft nicht zu stark zu beschleunigen, da der Luftwiderstand klein sein sollte. Das Ergebnis. In technischer Hinsicht ist es die Minimierung der Summe aus Schwerkraftverlust und aerodynamischem Verlust. Dasselbe gilt tatsächlich für die eigentliche Rakete, und bei der Festbrennstoffrakete wird der Schub auf ein gutes Gefühl auf dem Weg eingestellt. Die Lösung für das Goddard-Problem ist in Gebrauch! Optimierungsprobleme sind für die Welt nützlich! Beeindruckend!

knotting method Die Pseudospektralmethode, die den Inhalt von OpenGoddard enthält, ist ein großartiger Algorithmus, aber ich bin nicht gut in Zustandsvariablen und Steuervariablen, die nicht glatt (nicht differenzierbar) sind. Ich bin nicht gut darin, Steuervariablen diskontinuierlich zu ändern. Ich bin auch nicht gut in absoluten Werten. In Bezug auf das Goddard-Problem wird es nur so gelöst, dass Höhe, Geschwindigkeit, Gewicht und Schub glatt sind. Die Knotenmethode wird verwendet, um Lösungen für Zustandsvariablen und Steuervariablen zu finden, selbst wenn diese an einem bestimmten Punkt diskontinuierlich sind. Dies ist eine Methode zum Teilen des Berechnungsintervalls durch diskontinuierliche Teile. Open Goddard erleichtert die Verwendung der Knotenmethode. (Es gibt auch eine Algorithmusoptimierungssoftware, die den Abschnitt der Knotenmethode in der Welt automatisch unterteilt ...)

Goddard Problem (mit Knoten)

Listen Sie die Werte auf, die in die Problemklasse eingefügt werden sollen.

time_init = [0.0, 0.1, 0.3]
n = [25, 25]
num_states = [3, 3]
num_controls = [1, 1]

Außerdem wird angegeben, welche Bewegungsgleichung für jedes Intervall angewendet wird und ob die Zustandsvariablen stetig sind. Hier wird True mit der Erwartung ausgewählt, dass sich nur die Steuervariablen diskontinuierlich ändern. Das Richtig / Falsch hier und die Einschränkungsbedingung hängen eng zusammen. Geben Sie sie daher sorgfältig an. Wenn False, wird es divergieren, es sei denn, die Variable ist am Knotenpunkt in der Randbedingung (Gleichheit) festgelegt.

prob.dynamics = [dynamics, dynamics]
prob.knot_states_smooth = [True]

Von Oben,

Mit Knoten ist die maximale Höhe gesunken. .. .. Es war nicht sehr gut. Es ist nicht einfach gut, diese Knotenmethode so zu verwenden, aber es ist jetzt möglich, Probleme mit diskontinuierlichen Variablen zu behandeln.