Coursera-Herausforderungen beim maschinellen Lernen in Python: ex5 (Anpassung der Regularisierungsparameter)
Eine Reihe, die Matlab / Octave-Programmieraufgaben in Courseras Klasse für maschinelles Lernen (Professor Andrew Ng) in Python implementiert. Das Konzept bleibt gleich:
- Anstatt den Code der Aufgabe so zu reproduzieren, wie er ist, implementieren Sie ihn so effizient wie möglich mithilfe einer Python-Bibliothek wie scicit-learn.
Diese Woche (Woche 6) trägt den Titel "Ratschläge zur Anwendung des maschinellen Lernens". Anstatt ein neues Lernmodell zu lernen, lernen Sie, wie Sie Modellparameter optimieren und die Modellleistung überprüfen. Wenn ich diesem Thema eine Woche zuordne, denke ich, dass das Merkmal dieses Kurses ** "eher praktisch als theoretisch voreingenommen" ** erscheint.
Hier ist ein kurzer Blick darauf, wie Sie Ihr Modell optimieren können:
- Wenn Daten vorhanden sind, teilen Sie diese in Trainingsdaten, Kreuzvalidierungsdaten und Testdaten auf. Dr. Andrews Empfehlung ist ein Verhältnis von 6: 2: 2.
- Lernen mit verschiedenen Modellen und Parametern anhand von Trainingsdaten.
- Kreuztest, um festzustellen, welches Modell und welche Parameter gut sind. Zeichnen Sie zu diesem Zeitpunkt eine Lernkurve, um sie zu bestimmen. --Messen Sie die Leistung des zuletzt ermittelten Modells mit Testdaten.
Programmieraufgaben werden ebenfalls mit diesem Verfahren fortgesetzt.
Lesen Sie zuerst die Daten
Sie können matlab .mat-Formatdaten mit scio.loadmat () von scipy laden.
import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio
from sklearn import linear_model, preprocessing
# scipy.io.loadmat()Lesen Sie Matlab-Daten mit
data = scio.loadmat('ex5data1.mat')
X = data['X']
Xval = data['Xval']
Xtest = data['Xtest']
y = data['y']
yval = data['yval']
ytest = data['ytest']
Es scheint, dass diese Daten den Wasserstand von X = Damm verwenden, um die Wassermenge vorherzusagen, die aus y = Damm fließt.
Versuchen Sie zuerst die lineare Regression
Vorerst werde ich eine lineare Regression durchführen und diese zeichnen.
model = linear_model.Ridge(alpha=0.0)
model.fit(X,y)
px = np.array(np.linspace(np.min(X),np.max(X),100)).reshape(-1,1)
py = model.predict(px)
plt.plot(px, py)
plt.scatter(X,y)
plt.show()
Sie können das Modell "linear_model.LinearRegression ()" verwenden, das Sie immer verwenden, aber ich verwende das Modell "Ridge ()", da ich später einen Regularisierungsterm hinzufügen werde. In diesem Modell können Sie die Stärke der Regularisierung mit dem Parameter "alpha" angeben, aber mit "alpha = 0.0" gibt es keine Regularisierung, die mit dem Modell "LinearRegression ()" identisch ist.
Klicken Sie hier für die Ergebnisse.

Wie Sie sehen können, passen die Daten nicht gut zu geraden Linien.
Versuchen Sie dennoch, eine Lernkurve mit linearer Regression zu zeichnen
Versuchen Sie, eine Lernkurve zu zeichnen, indem Sie die Anzahl der Trainingsdaten ändern, obwohl Sie wissen, dass keine gerade Linie gilt. Führen Sie eine lineare Regression mit 1 bis 12 Trainingsdaten durch und zeichnen Sie die Fehler für die Trainingsdaten und die Fehler für die Kreuzvalidierungsdaten auf. "Fehler" ist der quadratische Fehler, der mit der folgenden Formel berechnet werden kann.
#Versuchen Sie, eine Lernkurve mit linearer Regression zu zeichnen
error_train = np.zeros(11)
error_val = np.zeros(11)
model = linear_model.Ridge(alpha=0.0)
for i in range(1,12):
#Führen Sie eine Regression mit nur i Teilmengen von Trainingsdaten durch
model.fit( X[0:i], y[0:i] )
#Berechnen Sie Fehler in i Teilmengen dieser Trainingsdaten
error_train[i-1] = sum( (y[0:i] - model.predict(X[0:i]))**2 ) / (2*i)
#Berechnen Sie den Datenfehler für den Kreuztest
error_val[i-1] = sum( (yval - model.predict(Xval) )**2 ) / (2*yval.size)
px = np.arange(1,12)
plt.plot(px, error_train, label="Train")
plt.plot(px, error_val, label="Cross Validation")
plt.xlabel("Number of training examples")
plt.ylabel("Error")
plt.legend()
plt.show()
Das Ergebnis ist so.

Selbst wenn die Trainingsdaten auf 12 (alle) erhöht werden, verringert sich der Fehler nicht sowohl für Zugdaten als auch für Kreuzvalidierungsdaten. Da dies beim linearen Regressionsmodell nicht der Fall ist, besteht der nächste Schritt darin, eine polymorphe Anpassung zu versuchen.
Polygonale Anpassung
Die oben implementierte lineare Regressionshypothese lautet
In scikit-learn gibt es eine Klasse namens "sklearn.preprocessing.PolynomialFeatures", die die Merkmale dieses Polynoms berechnet und erstellt. Wir werden diese also verwenden. Klicken Sie hier für den Code.
#Berechnen Sie den Multiplikator von X und dem neuen Merkmal X._Lass es poly sein
#X ist eine m x 1 Matrix, X._Poly ist eine m x 8-Matrix
poly = preprocessing.PolynomialFeatures(degree=8, include_bias=False)
X_poly = poly.fit_transform(X)
# X_Lineare Regression mit poly
model = linear_model.Ridge(alpha=0.0)
model.fit(X_poly,y)
#Handlung
px = np.array(np.linspace(np.min(X)-10,np.max(X)+10,100)).reshape(-1,1)
#Dieses Modell ist x_Da Poly als Eingabe akzeptiert wird, wird x zum Zeichnen auch in Form einer Skala erweitert.
px_poly = poly.fit_transform(px)
py = model.predict(px_poly)
plt.plot(px, py)
plt.scatter(X, y)
plt.show()
Klicken Sie hier für die Anpassungsergebnisse.

Die Anpassung mit einem Polypoly 8. Ordnung gilt für alle Trainingsdaten. Dies ist jedoch ein Übertraining und kann ein schlecht vorhersehbares Modell für neue Daten sein. Dieses Mal werden wir bei der Überprüfung dieses Modells mit den Daten für den Kreuztest die Regularisierungsparameter anpassen, indem wir den Regularisierungsterm einfügen.
Optimierung der Regularisierungsparameter
Durch Einbeziehung des Regularisierungsterms wird die Kostenfunktion der linearen Regression
$ \ Lambda $ im Molekül des zweiten Terms ist ein Parameter, der die Stärke der Regularisierung anpasst. Wie wir oben gesehen haben, entspricht dies dem Parameter "alpha" in "linear_model.Ridge ()". Ändern Sie diesen Parameter wie bei Coursera in 0,001, 0,003, 0,01, 0,03, 0,1, 0,3, 1, 3, 10 und zeichnen Sie die Lernkurve auf, um festzustellen, welches $ \ lambda $ für Sie geeignet ist.
Klicken Sie hier für den Code.
#Berechnen Sie den Multiplikator von X und dem neuen Merkmal X._Lass es poly sein
#X ist eine m x 1 Matrix, X._Poly ist eine m x 8-Matrix
poly = preprocessing.PolynomialFeatures(degree=8, include_bias=False)
X_poly = poly.fit_transform(X) #Trainingsdaten
Xval_poly = poly.fit_transform(Xval) #Kreuzvalidierungsdaten
#Versuchen Sie, eine Lernkurve zu zeichnen, indem Sie λ ändern
error_train = np.zeros(9)
error_val = np.zeros(9)
lambda_values = np.array([0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1.0, 3.0, 10.0])
for i in range(0,9):
# X_Lineare Regression mit poly
model = linear_model.Ridge(alpha=lambda_values[i]/10, normalize=True ) #Ändern Sie den Regularisierungsparameter Alpha
model.fit(X_poly,y)
#Berechnen Sie Fehler in Trainingsdaten (mit Regularisierungsbegriff)
error_train[i] = sum( (y - model.predict(X_poly))**2 ) / (2*y.size) + sum(sum( model.coef_**2 )) * lambda_values[i]/(2*y.size)
#Berechnen Sie den Fehler in den Daten für den Kreuztest (mit Regularisierungsterm).
error_val[i] = sum( (yval - model.predict(Xval_poly) )**2 ) / (2*yval.size) + sum(sum( model.coef_**2 ))* lambda_values[i]/(2*yval.size)
px = lambda_values
plt.plot(px, error_train, label="Train")
plt.plot(px, error_val, label="Cross Validation")
plt.xlabel("Lambda")
plt.ylabel("Error")
plt.legend()
plt.show()
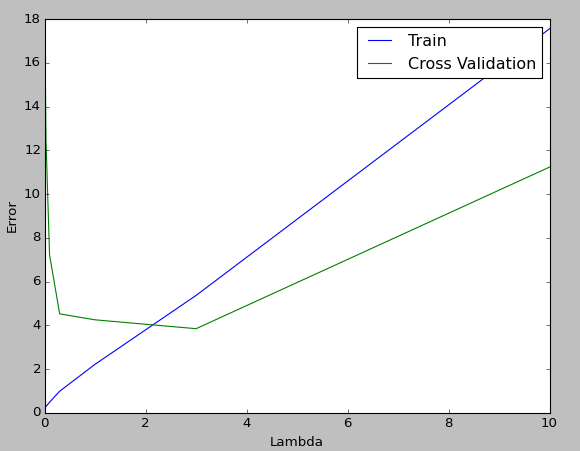
Die Darstellung sieht folgendermaßen aus, und das Ergebnis ist, dass $ \ lambda = 3 $, das im Kreuztest den kleinsten Fehlerwert aufweist, gut ist.
abschließend
sklearn.linear_model.Ridge () hat auch ein Modell namenssklearn.linear_model.RidgeCV ()für Kreuztests, und es scheint, dass es die optimale Alpha-Zahl zusammen berechnet, wenn es trainiert wird.
Verweise
- Erklärung von scikit-learn
- Auswirkung der L1-Regularisierung und der L2-Regularisierung im Regressionsmodell
Recommended Posts