Spielen Sie handschriftliche Zahlen mit Python Teil 2 (identifizieren)
Identifizieren Sie handschriftliche numerische Daten
Im vorherigen Artikel habe ich handgeschriebene numerische Daten gelesen und abgebildet und dann die Korrelation betrachtet, aber dieses Mal möchte ich die Nummer identifizieren.
Da es sich um eine handschriftliche Nummernidentifikation handelt, wird identifiziert, welcher der 10 Klassen von 0 bis 9 die angegebenen Daten entsprechen. So zuerst,
C = \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}
Definieren Sie 10 Klassen von.
Eine der Methoden des maschinellen Lernens heißt "überwachtes Lernen", und dieses Muster wird verwendet. Wenn ein Lehrer im Voraus eine bestimmte Anzahl korrekter Antwortdaten sammelt und analysiert, wird ein zur Identifizierung erforderlicher Diskriminator erstellt, und die Daten, die Sie tatsächlich identifizieren möchten, werden zur Identifizierung in diesen Diskriminator eingegeben. Es ist der Weg. Diese im Voraus vorbereiteten Daten werden als Lehrerdaten bezeichnet.
Vorlagenübereinstimmung
Dieses Mal möchte ich versuchen, Zahlen mithilfe der Template-Matching-Methode zu erkennen. Definieren Sie den repräsentativen Wert jedes Etiketts (hier die Nummern 0 bis 9) und erstellen Sie einen Klassifikator. Diesmal wird der Durchschnittswert der Lehrerdaten als repräsentativer Wert verwendet. Wir berechnen den Abstand zwischen diesem repräsentativen Wert und den zu identifizierenden übergebenen Daten und sagen, dass er zur Klasse des repräsentativen Werts mit dem kürzesten Abstand gehört.
Das letzte Mal habe ich mich mit handgeschriebenen numerischen Daten von "train_small.csv" befasst, aber diesmal ist es die vollständige Datenversion "train.csv" ( 42.000 Daten) werden als Lehrerdaten für das Lernen verwendet. Da die numerischen Daten 28x28-Bilddaten verwenden, können sie durch einen 784-dimensionalen Vektor dargestellt werden, und jede der Lehrerdaten ist
y_i= (y_1, y_2,...,y_{784}) (i=0,1,...,9)
Es wird ausgedrückt als. $ i $ ist eine Klasse für jede Zahl.
Hier wird der repräsentative Wert als $ \ hat {y} _i $ beschrieben.
Der repräsentative Wert einer Klasse mit der Nummer 8 ist beispielsweise $ \ hat {y} _8 $. Die repräsentativen Werte sind im Durchschnitt wie folgt.
$ n_i $ ist die Anzahl der Lehrerdaten für jede Nummer.
\hat{y}_i = \frac{1}{n_i}\sum_{j=1}^{n_i} y_j
Wenn nun die zu identifizierenden Zieldaten als $ x_j $ ausgedrückt werden
x_j= (x_1, x_2,...,x_{784})
Da es auch durch einen 784-dimensionalen Vektor als Diskriminator dargestellt wird
{\rm argmin}_i{({\rm distance}_i)} = {\rm argmin}_i{(\|\hat{y}_i - x_j\|)}
Wird genutzt.
Ableitung und Anzeige repräsentativer Werte
Ich werde tatsächlich berechnen. Importieren Sie zuerst die erforderlichen Bibliotheken.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from collections import defaultdict
Definieren Sie eine Funktion als Dienstprogramm. Die erste Ziffer ist die Beschriftung, und die folgenden sind die Daten, also die Funktion add_image (), die sie unterteilt und nach Klassen klassifiziert, die Funktion count_label (), die die Nummer jeder Beschriftung zählt, und plot_digits () für das Zeichnen von Diagrammen.
image_dict = dict()
def add_image(label, image_vector):
vec = np.array(image_vector)
if label in image_dict:
image_dict[label] += vec
else:
image_dict[label] = vec
return image_dict
label_dd = defaultdict(int)
def count_label(data):
for d in data:
label_dd[d[0]] += 1
return label_dd
def plot_digits(X, Y, Z, size_x, size_y, counter, title):
plt.subplot(size_x, size_y, counter)
plt.title(title)
plt.xlim(0,27)
plt.ylim(0,27)
plt.pcolor(X, Y, Z)
plt.gray()
plt.tick_params(labelbottom="off")
plt.tick_params(labelleft="off")
Erstellen Sie zunächst einen repräsentativen Wert $ \ hat {y} _i $ und zeigen Sie ihn als Bild an.
size = 28
raw_data= np.loadtxt('train_master.csv',delimiter=',',skiprows=1)
# draw digit images
plt.figure(figsize=(11, 6))
# data aggregation
for i in range(len(raw_data)):
add_image(raw_data[i,0],raw_data[i,1:785])
count_dict = count_label(raw_data)
standardized_digit_dict = dict() #Wörterbuchobjekt, das repräsentative Werte speichert
count = 0
for key in image_dict.keys():
count += 1
X, Y = np.meshgrid(range(size),range(size))
num = label_dd[key]
Z = image_dict[key].reshape(size,size)/num
Z = Z[::-1,:]
standardized_digit_dict[int(key)] = Z
plot_digits(X, Y, standardized_digit_dict[int(key)], 2, 5, count, "")
plt.show()

Als ich das letzte Mal einzelne Daten visualisierte und anzeigte, gab es einige, bei denen es sich anscheinend nicht um Zahlen handelte. Wenn Sie jedoch viele Daten überlagern und den Durchschnitt ermitteln, werden schöne Zahlen angezeigt. Dies wird als repräsentativer Wert für jede Klasse verwendet und mit den zu identifizierenden Daten verglichen.
Identifikation durchführen: Versuchen Sie es zuerst mit einem
Es ist schließlich die Ausführung der Identifizierung. Zunächst möchte ich sehen, wie groß der Abstand zwischen den Identifikationszieldaten und dem repräsentativen Wert jeder Klasse ist, um das Bild zu erfassen. Die Identifikationszieldaten werden von Kaggle heruntergeladen. Verwenden Sie test.csv auf der Datenseite (https://www.kaggle.com/c/digit-recognizer/data). Da es einige gibt, bereiten wir die Daten vor, die aus den ersten 200 extrahiert wurden (test_small.csv).
test_data= np.loadtxt('test_small.csv',delimiter=',',skiprows=1)
# compare 1 tested digit vs average digits with norm
plt.figure(figsize=(10, 9))
for i in range(1): #Versuchen Sie nur den ersten
result_dict = defaultdict(float)
X, Y = np.meshgrid(range(size),range(size))
Z = test_data[i].reshape(size,size)
Z = Z[::-1,:]
flat_Z = Z.flatten()
plot_digits(X, Y, Z, 3, 4, 1, "tested")
count = 0
for key in standardized_digit_dict.keys():
count += 1
X1 = standardized_digit_dict[key]
flat_X1 = standardized_digit_dict[key].flatten()
norm = np.linalg.norm(flat_X1 - flat_Z) #Ableitung des Abstands zwischen jedem repräsentativen Wert und den zu identifizierenden Daten
plot_digits(X, Y, X1, 3, 4, (1+count), "d=%.3f"% norm)
plt.show()
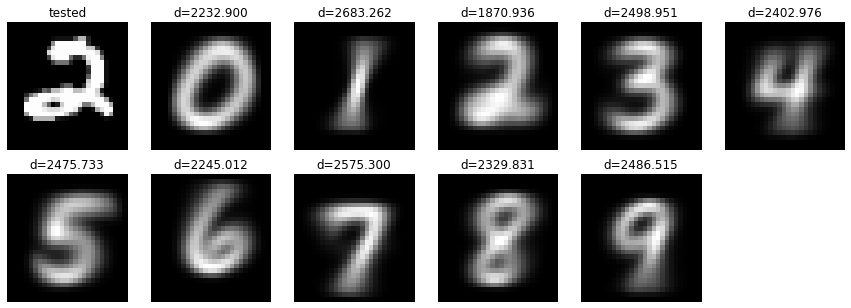
Die Identifikationszieldaten sind "2", aber was ist mit dem Ergebnis? Der Abstand wird über jedem Bild angezeigt. Bei dieser Zahl ist d = 1870.936 über "2" die kleinste! Identifikation ist erfolgreich! : entspannt:
Ausführung der Identifikation: Identifikationsergebnis von 200 Daten
Lassen Sie uns nun 200 Daten identifizieren und sehen, wie genau sie sind.
# recognize digits
plt.figure(figsize=(15, 130))
for i in range(len(test_data)):
result_dict = defaultdict(float)
X, Y = np.meshgrid(range(size),range(size))
tested = test_data[i].reshape(size,size)
tested = tested[::-1,:]
flat_tested = tested.flatten()
norm_list=[]
count = 0
for key in standardized_digit_dict.keys():
count += 1
sdd = standardized_digit_dict[key]
flat_sdd = sdd.flatten()
norm = np.linalg.norm(flat_sdd - flat_tested)
norm_list.append((key, norm))
norm_list = np.array(norm_list)
min_result = norm_list[np.argmin(norm_list[:,1])]
plot_digits(X, Y, tested, 40, 5, i+1, "l=%d, n=%d" % (min_result[0], min_result[1]))
plt.show()
Ich habe versucht, 200 Identifikationszieldaten auf dieses Identifikationsgerät anzuwenden, und die korrekte Antwortrate betrug 80% (160/200), was ein schlechtes Ergebnis war! : smile: Ist es nicht ein gutes Ergebnis für die einfache Methode, nur den Abstand vom Durchschnittswert zu messen? In der folgenden Abbildung finden Sie aktuelle Detaildaten.

Bei der Analyse der Fälle, die nicht identifiziert werden konnten, war es besonders schwierig, zwischen 4 und 9 zu unterscheiden, und es traten 6 Identifikationsfehler auf. Als nächstes sind 1-7, 1-8, 3-5, 3-8, 3-9, 8-9 jeweils drei Fehler. Immerhin sehen die Zahlen etwas ähnlich aus.
** Zusammenfassung des Identifikationsfehlers **
| combination of label | count |
|---|---|
| 4-9 | 6 |
| 1-7 | 3 |
| 1-8 | 3 |
| 3-5 | 3 |
| 3-8 | 3 |
| 3-9 | 3 |
| 8-9 | 3 |
| 2-3 | 2 |
| 4-6 | 2 |
| 0-2 | 1 |
| 0-3 | 1 |
| 0-4 | 1 |
| 0-5 | 1 |
| 0-8 | 1 |
| 1-2 | 1 |
| 1-3 | 1 |
| 1-5 | 1 |
| 2-7 | 1 |
| 2-8 | 1 |
| 4-7 | 1 |
| 5-9 | 1 |
Übersicht über die Template-Matching-Methode
Abschließend möchte ich einen kurzen Überblick über die Template-Matching-Methode geben. Die numerischen Daten sind diesmal 28x28 784-dimensionale Daten und die Anzahl der Dimensionen ist hoch, so dass sie nicht grafisch dargestellt werden können, aber ich werde es erklären, als ob es zweidimensional wäre, um ein Bild zu ergeben. Siehe das Streudiagramm unten. Die Daten für jede Zahlenklasse können durch Farbe unterschieden werden, und die Daten werden gestreut. Dies ist ein Bild einer Reihe von Lehrerdaten. Nehmen Sie dies als repräsentativen Wert und mitteln Sie ihn. Typische Werte werden durch etwas größere Punkte in der Grafik dargestellt.

Wenn beispielsweise der schwarze Punkt unten die Identifikationszieldaten sind, ist der nächste repräsentative Wert der repräsentative Wert der Klasse "7", so dass diese Identifikationszieldaten als Klasse "7" identifiziert werden. Dies ist die diesmal verwendete Template-Matching-Methode.

Recommended Posts