[PYTHON] Lineare Regression mit Statistikmodellen

Früher habe ich scipy.stats.linregress als lineare Regression von Python verwendet, aber ich habe Statistikmodelle eingeführt, da es nur wenige Funktionen hat und schwierig zu verwenden ist. Ich habe es nur 2 Stunden lang benutzt, daher habe ich möglicherweise etwas grundlegend falsch verstanden. Ich habe es nur 2 Stunden lang benutzt, es tut mir leid

Im Folgenden wird beschrieben, wie OLS (gewöhnliche Methode der kleinsten Quadrate; gewöhnliche Methode der kleinsten Quadrate) von Statistikmodellen verwendet wird. Klicken Sie hier für offizielle Materialien http://statsmodels.sourceforge.net/stable/regression.html

Installation

Normalerweise mit pip.

$ sudo pip install statsmodels

Der folgende Code verwendet auch numpy und matplotlib. Installieren Sie sie also, wenn Sie sie nicht haben.

$ sudo pip install numpy
$ sudo pip install matplotlib

Einfaches Beispiel

Vorerst als einfachstes Beispiel

y = a + bx + \varepsilon

Betrachten Sie die lineare Regression im Modell. Mit anderen Worten, wenn die Daten von $ (x_i, y_i) $ gegeben sind, wird der Parameter $ (a, b) $ bestimmt, so dass der Fehler $ \ sum \ varepsilon_i ^ 2 $ minimiert wird.

Angenommen, Sie haben die folgenden Daten. Dies sind die Daten, die ich jetzt gemacht habe, und wenn ich zuerst geantwortet hätte, wäre es "a = 1,0, b = 3,0", aber ich gebe vor, ich weiß es nicht und finde es durch Regression.

data.txt

#      x        y
  -1.000   -1.656
  -0.900   -0.734
  -0.800   -3.036
  -0.700   -1.026
  -0.600   -1.104
  -0.500    0.023
  -0.400    0.246
  -0.300    1.817
  -0.200    0.651
  -0.100    0.082
  -0.000    2.524
   0.100    2.231
   0.200    0.783
   0.300    2.489
   0.400    1.892
   0.500    3.207
   0.600    1.868
   0.700    3.954
   0.800    4.447
   0.900    4.024

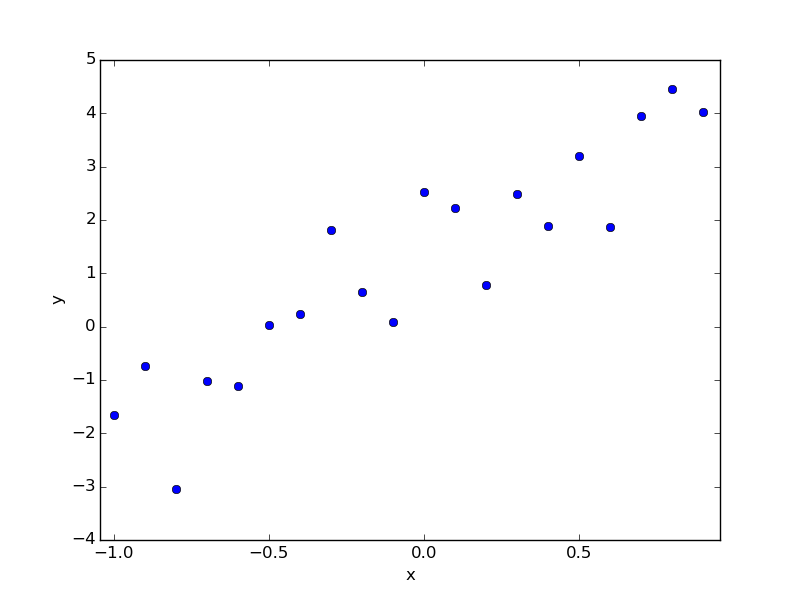
Die Rückkehr dazu ist wie folgt.

regression.py

# coding: utf-8
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

#Daten lesen
data = np.loadtxt("data.txt")
x = data.T[0]
y = data.T[1]

#Anzahl von Beispielen
nsample = x.size

#Magie(Kommentar später)
X = np.column_stack((np.repeat(1, nsample), x))

#Regressionsausführung
model = sm.OLS(y, X)
results = model.fit()

#Ergebniszusammenfassung anzeigen
print results.summary()

#Parameterschätzungen abrufen
a, b = results.params

#Handlung anzeigen
plt.plot(x, y, 'o')
plt.plot(x, a+b*x)
plt.text(0, 0, "a={:8.3f}, b={:8.3f}".format(a,b))
plt.show()

Bei der Ausführung werden der folgende Text und das folgende Diagramm angezeigt.

                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.831
Model:                            OLS   Adj. R-squared:                  0.822
Method:                 Least Squares   F-statistic:                     88.59
Date:                Thu, 25 Dec 2014   Prob (F-statistic):           2.25e-08
Time:                        14:07:16   Log-Likelihood:                -24.450
No. Observations:                  20   AIC:                             52.90
Df Residuals:                      18   BIC:                             54.89
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [95.0% Conf. Int.]
------------------------------------------------------------------------------
const          1.2922      0.194      6.647      0.000         0.884     1.701
x1             3.1611      0.336      9.412      0.000         2.455     3.867
==============================================================================
Omnibus:                        0.801   Durbin-Watson:                   2.495
Prob(Omnibus):                  0.670   Jarque-Bera (JB):                0.653
Skew:                          -0.402   Prob(JB):                        0.721
Kurtosis:                       2.628   Cond. No.                         1.74
==============================================================================

Warnings:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Es wird so sein.

Lineares Basisfunktionsmodell

In dem oben erwähnten Modell war die Beziehung zwischen x und y ein linearer Ausdruck, aber im Leben möchten wir oft eine kompliziertere Beziehung zwischen x und y betrachten. Durch Verwendung eines linearen Basisfunktionsmodells wird es daher möglich, eine relativ unterschiedliche Beziehung zwischen x und y auszudrücken.

y = \beta_0 + \beta_1 \phi_1(x) + \beta_2\phi_2(x) + \cdots + \beta_{M-1}\phi_{M-1}(x) + \varepsilon

Hier sind $ x und y $ Daten, $ \ phi_j (x) $ ist eine bekannte Funktion und $ \ beta_j $ ist ein zu erhaltender Parameter. Beachten Sie, dass diese Formel leicht auf $ \ phi_0 (x) \ equiv 1 $ gesetzt werden kann.

y = \sum_{j=0}^{M-1} \beta_j\phi_j(x) + \varepsilon

Kann auch geschrieben werden. Wenn zum Beispiel $ M = 3, \ phi_1 (x) = x, \ phi_2 (x) = x ^ 2 $, dann ist die quadratische Funktion $ y = \ beta_0 + \ beta_1x + \ beta_2x ^ 2 + \ varepsilon $ ..

Wenn Sie eine Regression mit Statistikmodellen durchführen, müssen Sie nur die Informationen für die Daten $ (x_i, y_i) $ und die bekannte Funktion $ \ phi_j (x) $ eingeben, aber es ist umständlich, die Funktionsinformationen direkt zu stecken, also $ Geben Sie die folgende Matrix ein, die die Informationen von x_i $ und $ \ phi_j (x_i) $ zusammenfasst. (Wenn M = 3)

X = \begin{Bmatrix}
\phi_0(x_0) & \phi_1(x_0) & \phi_2(x_0) \\
\phi_0(x_1) & \phi_1(x_1) & \phi_2(x_1) \\
\phi_0(x_2) & \phi_1(x_2) & \phi_2(x_2) \\
& \vdots & \\
\end{Bmatrix}

Hier ist $ \ phi_0 (x) \ equiv 1 $, also ist die erste Spalte dieser Matrix alle 1. Deshalb habe ich die Spalte `np.repeat (1, nsample)` im vorherigen Code als "magic" hinzugefügt.

Wenn wir also die Art und Weise ändern, wie diese Matrix X erstellt wird, ist eine lineare Regression eines beliebigen Modells möglich.

Etwas kompliziertes Beispiel

Als Beispiel

y = a + bx + cx^2 + \varepsilon

Betrachten Sie das Modell. Alles, was Sie tun müssen, ist, dem Teil der Matrix X im vorherigen Code eine Spalte hinzuzufügen, die $ x ^ 2 $ entspricht. Bereiten Sie zunächst den Datensatz vor. Wie üblich lautet die Antwort "a = 3,0, b = 1,0, c = 2,0".

data.txt

#      x        y
  -2.000   10.260
  -1.800    7.403
  -1.600    7.779
  -1.400    4.310
  -1.200    4.051
  -1.000    4.577
  -0.800    3.416
  -0.600    3.628
  -0.400    3.968
  -0.200    3.780
  -0.000    1.873
   0.200    2.741
   0.400    2.106
   0.600    5.286
   0.800    8.138
   1.000    5.316
   1.200    9.159
   1.400    9.748
   1.600    7.585
   1.800   10.726

Der Code ist unten. Ich habe jedoch nur den Teil geändert, in dem die Matrix X erstellt wurde, und die Anzahl der letzten Parameter.

regression_2.py

# coding: utf-8
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt

#Daten gelesen
data = np.loadtxt("data.txt")
x = data.T[0]
y = data.T[1]

#Anzahl von Beispielen
nsample = x.size

#Matrix X erstellen
X = np.column_stack((np.repeat(1, nsample), x, x**2))

#Führen Sie eine Regression durch
model = sm.OLS(y, X)
results = model.fit()

#Ergebniszusammenfassung anzeigen
print results.summary()

#Parameterschätzungen abrufen
a, b, c = results.params

#Anzeige als Grafik
plt.plot(x, y, 'o')
plt.plot(x, a+b*x+c*x**2)
plt.title("a={:.4f}, b={:.4f}, c={:.4f}".format(a,b,c))
plt.show()

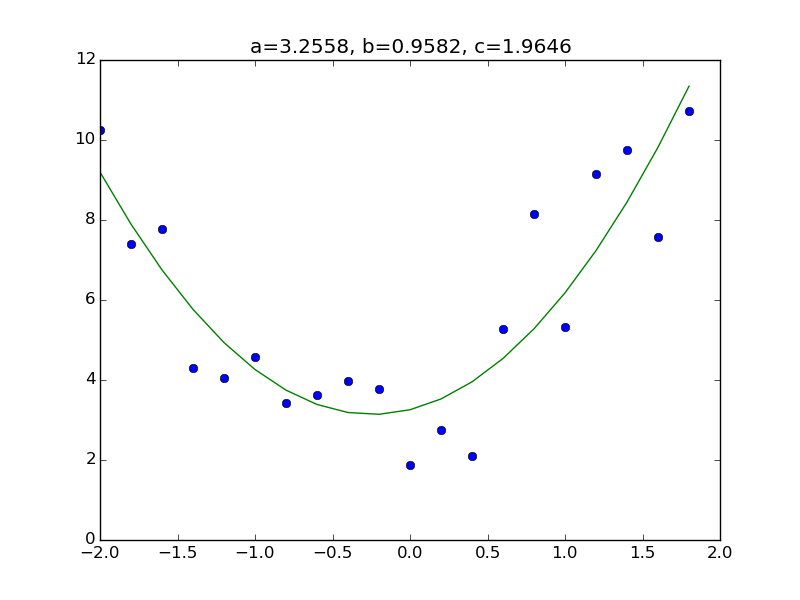
Andere

Zusätzlich zu OLS (gewöhnliche Minimum-Square-Methode) verfügt statsmodels auch über WLS (Weighted Minimum Square-Methode). Schreiben Sie es also, wenn Sie Lust dazu haben.