[PYTHON] Plattenreproduktion der Bayes'schen linearen Regression (PRML §3.3)

Gruß

Ich bin @naoya_t, die Sekretärin des Adventskalenders 2013 für maschinelles Lernen, der heute begonnen hat. Ich freue mich darauf, dieses Jahr wieder mit Ihnen zusammenzuarbeiten. (Der Tag hat sich in Japan geändert. Es tut mir leid, dass es so spät war. Ich war gerade rechtzeitig zur argentinischen Standardzeit (GMT-3)!)

Der Inhalt dieses Adventskalender-Artikels ist für alle datenwissenschaftlichen Aspekte wie Mustererkennung, maschinelles Lernen, Verarbeitung natürlicher Sprache und Data Mining in Ordnung. Der Betrag spielt keine Rolle, solange er dem Thema folgt. (Zusammenfassung der gelesenen Teile wie PRML, MLaPP usw., die implementiert werden sollen, Papiereinführung, Formelentwicklung usw.)

Lassen Sie uns zusammen mit allen, die schreiben und allen, die nur lesen, genießen!

Das heutige Thema

Da es sich heute um ein leichtes Thema aus PRML handelt, das jeder liebt, möchte ich Abbildung 3.8 und Abbildung 3.9 aus "Bayes Linear Regression" in §3.3 wiedergeben.

図3.8 図3.9

Ich dachte daran, ein 3D-Diagramm des entsprechenden Kernels zu zeichnen (Abb. 3.10), aber die Zeit war abgelaufen. (Ich werde es hinzufügen, wenn ich Lust dazu habe!)

Erforderliche Berechnung

Die Beschriftung in Abbildung 3.8 besagt, dass "das Modell aus neun Gaußschen (Basis-) Funktionen der Form (3.4) besteht". Gaußsche Basisfunktion $ \ phi_j (x) = exp \ left (- \ frac {(x- \ mu_j) ^ 2} {2s ^ 2} \ right) $ im Bereich von x = [0,1] Ich werde versuchen, 9 davon gleichmäßig zu arrangieren.

Figur 3.8 ist die vorhergesagte Verteilungp(t|\mathbf{x},\mathbf{t},\alpha,\beta)=N(t|\mathbf{m}_N\mathbf{\phi(x)},\sigma_N^2(\mathbf{x})) (3.58)Sie können zeichnen, wenn Sie den Durchschnitt und die Varianz von erhalten können. Wird dafür benötigt $ \ mathbf {m} _N $, $ \ mathbf {S} _N $, $ \ sigma_N ^ 2 (\ mathbf {x}) $

\mathbf{S}_N^{-1}=\alpha I+\beta\Phi^\mathrm{T}\Phi (3.54)
\mathbf{m}_N=\beta\mathbf{S}_N\Phi^\mathrm{T}\mathbf{t} (3.53)
\sigma_N^2(\mathbf{x})=\frac1\beta+\mathbf{\phi(x)}^\mathrm{T}\mathbf{S}_N\mathbf{\phi(x)} (3.59)

Es kann von gefunden werden. Das hier angezeigte $ \ Phi $ ist die Planungsmatrix (3.16), mit der jeder vertraut ist. Stellen Sie aus der Basisfunktion $ \ phi_j (x) $ und den Eingabedaten $ \ mathbf {x} $ zusammen.

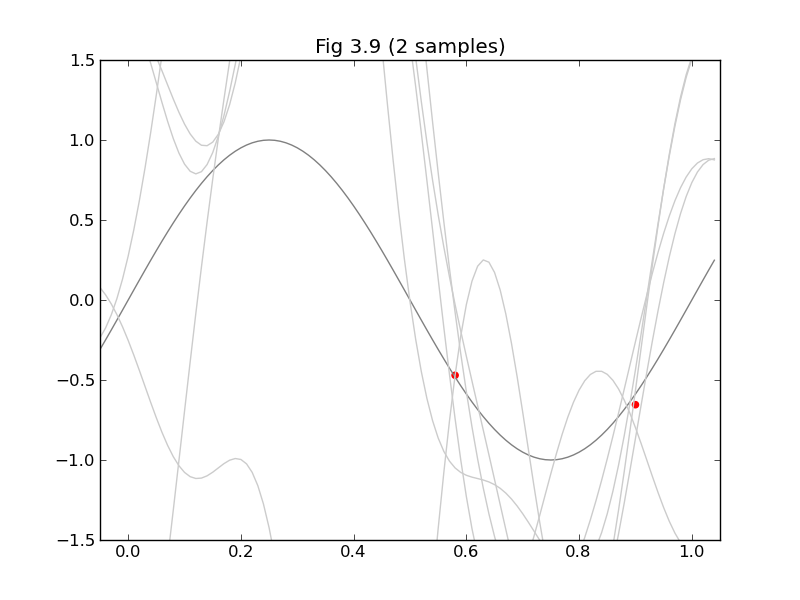
Figur 3.9 ist\mathbf{w}Posteriore Verteilung vonp(\mathbf{w}|\mathbf{t})=N(\mathbf{w}|\mathbf{m}_N,\mathbf{S}_N) (3.49)Von\mathbf{w}Probenahme von jeweils 5, ungefähr jedery(x,\mathbf{w})=\mathbf{w}^\mathrm{T}\mathbf{\phi(x)}Einfach planen.

Code

`fig38_39.py`


#!/usr/bin/env python
# -*- coding: utf-8 -*-

from pylab import *

S     = 0.1
ALPHA = 0.1
BETA  = 9

def sub(xs, ts):
    # φj(x)Übernimmt die Gaußsche Basisfunktion
    def gaussian_basis_func(s, mu):
        return lambda x:exp(-(x - mu)**2 / (2 * s**2))

    # φ(x)
    def gaussian_basis_funcs(s, xs):
        return [gaussian_basis_func(s, mu) for mu in xs]

    xs9 = arange(0, 1.01, 0.125) # 9 points
    bases = gaussian_basis_funcs(S, xs9)

    N = size(xs) #Datenbewertung
    M = size(bases) #Anzahl der Basisfunktionen

    def Phi(x):
        return array([basis(x) for basis in bases])

    # Design matrix
    PHI = array(map(Phi, xs))
    PHI.resize(N, M)

    # predictive distribution
    def predictive_dist_func(alpha, beta):
        S_N_inv = alpha * eye(M) + beta * dot(PHI.T, PHI)
        m_N = beta * solve(S_N_inv, dot(PHI.T, ts)) # 20.1

        def func(x):
            Phi_x = Phi(x)
            mu = dot(m_N.T, Phi_x)
            s2_N = 1.0/beta + dot(Phi_x.T, solve(S_N_inv, Phi_x))
            return (mu, s2_N)

        return m_N, S_N_inv, func

    xmin = -0.05
    xmax =  1.05
    ymin = -1.5
    ymax =  1.5

    #
    #Figur 3.8
    #
    clf()
    axis([xmin, xmax, ymin, ymax])
    title("Fig 3.8 (%d sample%s)" % (N, 's' if N > 1 else ''))

    x_ = arange(xmin, xmax, 0.01)
    plot(x_, sin(x_*pi*2), color='gray')

    m_N, S_N_inv, f = predictive_dist_func(ALPHA, BETA)

    y_h = []
    y_m = []
    y_l = []
    for mu, s2 in map(f, x_):
        s = sqrt(s2)
        y_m.append(mu)
        y_h.append(mu + s)
        y_l.append(mu - s)

    fill_between(x_, y_h, y_l, color='#cccccc')
    plot(x_, y_m, color='#000000')

    scatter(xs, ts, color='r', marker='o')
    show()

    #
    #Figur 3.9
    #
    clf()
    axis([xmin, xmax, ymin, ymax])
    title("Fig 3.9 (%d sample%s)" % (N, 's' if N > 1 else ''))

    x_ = arange(xmin, xmax, 0.01)
    plot(x_, sin(x_*pi*2), color='gray')

    for i in range(5):
        w = multivariate_normal(m_N, inv(S_N_inv), 1).T
        y = lambda x: dot(w.T, Phi(x))[0]
        plot(x_, y(x_), color='#cccccc')

    scatter(xs, ts, color='r', marker='o')
    show()


def main():
    #Beispieldaten (fügt Gaußsches Rauschen hinzu)
    xs = arange(0, 1.01, 0.02)
    ts = sin(xs*pi*2) + normal(loc=0.0, scale=0.1, size=size(xs))

    #Nehmen Sie eine entsprechende Nummer aus den Probendaten
    def randidx(n, k):
        r = range(n)
        shuffle(r)
        return sort(r[0:k])

    for k in (1, 2, 5, 20):
        indices = randidx(size(xs), k)
        sub(xs[indices], ts[indices])


if __name__ == '__main__':
    main()

erledigt!

Am Ende

Letztes Jahr wurde darauf hingewiesen, dass ich vom ersten Tag an zu viel übersprungen habe, was nicht an der Zeit des Schreibens liegt, aber dieses Jahr tut es mir leid, dass ich nicht alle Erwartungen mit einer etwas leichteren Themeneinstellung erfüllen konnte ＞＜

Die verantwortliche Person für 12/2 ist @ puriketu99. Bleib dran!