Von Robotern über selbstfahrende Autos bis hin zu Spielen wie Go und Shogi werden heutzutage viele "KI" immer beliebter.

Eines der Schlüsselwörter ist "Stärkung des Lernens". In diesem Sinne ist es möglicherweise die auffälligste (und übertriebenste ...) Methode aller Methoden des maschinellen Lernens.

Diesmal über die Methode zur Stärkung des Lernens, Deep Q-Learning (sogenanntes Dokyun, DQN, das in letzter Zeit eine bemerkenswerte Genauigkeit der Grundlagen erreicht hat. )) Möchte ich den Ablauf und den Mechanismus seiner Entwicklung erläutern.

** Basierend auf dem Inhalt dieses Artikels wurde eine praktische Veranstaltung abgehalten (erweiterte und überarbeitete Version von PyConJP Talk) **

Stärkung des Lernens ab Python OpenAI Gym zum Anfassen

Die Vorlesungsmaterialien sind reich an Abbildungen, daher wird dies für Formeln und andere Dinge empfohlen.

Merkmale des verstärkenden Lernens

Intensiviertes Lernen ähnelt dem überwachten Lernen, liefert jedoch keine klare "Antwort" (durch den Lehrer). Was also präsentiert wird, sind "Aktionsoptionen" und "Belohnungen".

Wenn Sie dies als Antwort = Belohnung betrachten, haben Sie vielleicht das Gefühl, dass es dasselbe ist (Aktion A = 10pt usw.), aber es gibt einen großen Unterschied. Das heißt, die Belohnung für das Lernen zur Stärkung wird nicht "jeder Aktion" gegeben, sondern "dem Ergebnis kontinuierlicher Aktionen". Im Fußball ist ein Punkt für ein Tor eine Belohnung für die Stärkung des Lernens. Es wird jedoch keine Belohnung für jede Aktion des Passierens oder Dribbelns gegeben, um das Ziel zu erreichen. Auf der anderen Seite ist angewiesenes Lernen, wenn Anweisungen von außerhalb des Gerichts gesendet werden und sagen: "Der aktuelle Pass ist gut!" Und "Sie sollten dort nicht dribbeln!" Beim verstärkten Lernen wird nur ein Ziel als "Ergebnis kontinuierlicher Aktion" belohnt. Wie gut der Pass und das Dribbeln sind, um ihn zu erreichen, hängt von dem Fall ab, in dem das Ziel erreicht wurde, und dem Fall, in dem es nicht möglich war. Sie müssen die "Bewertung" selbst durchführen.

Wie "bewerten" Sie jede Aktion? Zunächst wird die Aktion (letzter Schuss) zum Zeitpunkt des Tores belohnt (1 Punkt). Aber was ist mit der Aktion kurz davor? Dies war auch die letzte Einstellung, um ein Tor zu erzielen. Ich denke, es war ein ziemlich guter Schachzug. Wenn Sie dann von der vorherigen zurückrechnen, können Sie jede Aktion rückwirkend von der letzten Aktion aus bewerten.

Beim intensiven Lernen wird die "Bewertung" jeder Aktion von sich aus anhand der Belohnung für das "Ergebnis kontinuierlicher Aktionen" auf diese Weise aktualisiert. Auf diese Weise lernen Sie fortlaufende Aktionen, auch wenn Sie nicht für jede Aktion einzeln eine Belohnung festlegen, und erhalten schließlich eine Belohnung, die auf Ihrer eigenen Bewertung basiert. Bei komplexen Spielen wie Shogi und Go kann es schwierig sein, zu entscheiden, welcher Zug in welcher Situation am besten ist, geschweige denn, wie viele Punkte die Belohnung haben sollte. Selbst in solchen Fällen ist der endgültige Gewinn oder Verlust klar, sodass Sie das Verstärkungslernen anwenden können, um die Schwierigkeit der Verhaltensbewertung zu überspringen und das endgültige Gewinnverhalten zu lernen. Infolgedessen kann verbessertes Lernen im Allgemeinen komplexere Probleme bewältigen als überwachtes Lernen.

Bitte beachten Sie jedoch, dass dies nicht bedeutet, dass verbessertes Lernen eine bessere Methode ist als überwachtes Lernen. Um es anders herum auszudrücken: Die Stärkung des Lernens nimmt viel Zeit in Anspruch, da Sie ohne klare Anweisungen eine "Bewertung des Verhaltens" in sich selbst erwerben müssen. Die Anzahl der Aktionen zum Erreichen des Ziels und die Anzahl der Kombinationen davon ist enorm, und die Optimierung nimmt viel Zeit in Anspruch (obwohl Computer rechenschnell sind). Darüber hinaus gibt es aus menschlicher Sicht keine rationale Garantie dafür, dass die durch die Stärkung des Lernens erworbene "Bewertung des Verhaltens" erreicht wird. Es ist klar, dass es einen richtigen Lehrer gibt und dass der erstere effizienter und einfacher zu erreichen ist, wenn Sie selbst lernen. Daher müssen Sie die Lernmethode entsprechend dem Problem auswählen, mit dem Sie sich befassen.

Das Obige sind die Merkmale eines verbesserten Lernens. Als nächstes werde ich dies modellieren und erklären, wie man es lernt.

Modellierung des verstärkenden Lernens (Markov-Entscheidungsprozess)

Das Problem des intensiven Lernens wird wie folgt modelliert.

States: S
Status. Im Spiel repräsentiert es einen bestimmten Aspekt
Model: T(s, a, s') (=P(s'|s, a))
T ist Übergang, und wenn Sie in Situation s Maßnahmen ergreifen, befinden Sie sich in Situation s '. Es ist jedoch ein probabilistischer Ausdruck (P (s '| s, a)), da er eine Situation ausdrückt, in der selbst wenn a ausgewählt ist, es nicht aktiviert wird oder an einen anderen Ort geht.
Actions: A(s), A
Aktion. Wenn sich die Aktion, die ausgeführt werden kann, je nach Situation ändert, wird sie zu einer Funktion wie A (s).
Reward: R(s), R(s, a), R(s, a , s')
Situationen und Belohnungen von Aktionen in diesen Situationen. Diese Belohnung wird bis auf das Endergebnis (sofortige Belohnung) selbst bewertet.
Policy: \pi(s) -> a
Strategie. Eine Funktion, die zurückgibt, welche Aktion a in der Situation s ausgeführt werden soll.

Diese Modellierung wird als Markov-Entscheidungsprozess (MDP, Markov-Entscheidungsprozess) bezeichnet. Markov bedeutet Markov-Natur und repräsentiert die Eigenschaft, dass nur die aktuellen Zustände an der nächsten Aktion beteiligt sind, wie durch $ \ pi (s) $ dargestellt.

Um es als Straßenkämpfer zu erklären, sieht es wie folgt aus.

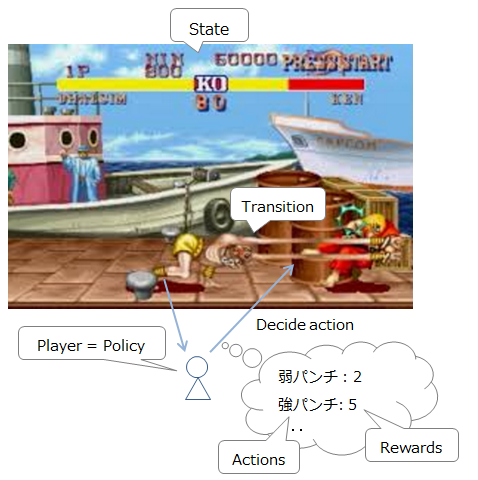
Aktuelle Situation (Feind / eigene Position und HP): Zustand
Derzeit verfügbare Befehle: Aktionen
Bewegung / Angriff usw .: T (s, a, s ') Liste der Befehle, die eingegeben werden können, und deren Aktivierungswahrscheinlichkeiten (da Sie einen Befehl möglicherweise verpassen, selbst wenn Sie versuchen, ein Yoga-Feuer auszulösen, wird er wahrscheinlich)
Spieler (Entscheidungsperson): Richtlinie
Belohnung für Aktion: Belohnung
Außerdem erhielt ich den Kommentar "Ich wollte, dass du durch maschinelles Lernen den stärksten Strike 2-Krieger machst", aber die Kampffähigkeit der KI hat bereits die der normalen Menschen übertroffen, und im Gegenteil, "wie man sich anpasst" ist ein Problem. (Referenz). Die Menschheit muss hart am Training arbeiten.

Übrigens ist es im Straßenkampf der kürzeste Weg, die HP des Gegners zu rasieren, um zu gewinnen, aber es ist klar, dass es am Ende schwierig ist, selbst mit nur einem Schlag zu gewinnen. Um die Strategie zu optimieren, ist es daher notwendig, die Belohnung langfristig und nicht kurzfristig zu maximieren.

Wenn die Zeit jedoch auch über einen längeren Zeitraum unendlich ist, ist das Stanzen mit dem Zoom (siehe Abbildung oben) die effizienteste Strategie aus möglichst großer Entfernung. Dies liegt daran, dass es sicherer ist, Maßnahmen zu ergreifen, die sich zumindest vom Gegner fernhalten, wenn Sie unendlich viel Zeit haben, als das Risiko einzugehen, sich Yoga-Flammen zu nähern und sie zu machen. Auf diese Weise tendiert die Zeit, wenn sie unendlich ist, dazu, sich auf ein risikoarmes Verhalten mit geringer Rendite zu konzentrieren. Daher werden wir das Konzept des zeitlichen Abschlags einführen. Mit anderen Worten, wenn Sie nicht schnell handeln, erhalten Sie immer weniger Belohnung für dieselbe Aktion.

Mit anderen Worten, die folgenden zwei Punkte sind wichtig für die Optimierung der Strategie.

Versuchen Sie, die Summe der Belohnungen zu optimieren
Führen Sie im Laufe der Zeit einen Prämienrabatt ein

Dies kann als Ausdruck wie folgt ausgedrückt werden.

U^{\pi}(s) = E \left[ \sum_{t}^{\infty} \gamma^{t} R(s_t) | \pi, s_0=s \right]

Summe der Belohnungen = $ U ^ {\ pi} (s) $: Summe der Belohnungen bei der Ausführung der Strategie $ \ pi $ aus dem Zustand $ s $ ($ \ pi, s_0 = s $)
Pünktlicher Rabatt = $ \ gamma $: $ 0 \ leq \ gamma <1 $, ein Wert nahe 1

Ziel ist es, eine Strategie zu finden, die diese "Summe der Belohnungen unter Berücksichtigung von Zeitrabatten" maximiert. Nennen wir diese optimale Strategie $ \ pi ^ * $. In der besten Strategie sollten Sie grundsätzlich handeln, um Ihre Belohnung zu maximieren. Dies kann mathematisch wie folgt ausgedrückt werden.

\pi^{*}(s) = argmax_a \sum_{s'} T(s, a, s') U(s')

$ argmax $ bedeutet, dass Sie den größten auswählen. Mit anderen Worten, von $ s '$, dem Übergangsziel von $ s $, wirkt sich die erwartete Gesamtbelohnung $ U (s') $ auf das Maximum von $ s '$ aus. Schließlich besteht die optimale Strategie $ \ pi ^ * $ darin, so zu handeln, dass die Summe der Belohnungen von jedem $ s $ maximiert wird, so dass $ U ^ {\ am Anfang definiert wird Sie können pi} (s) $ wie folgt umschreiben:

U(s) = R(s) + \gamma max \sum_{s'} T(s, a, s') U(s')

Diese Gleichung heißt ** Bellman-Gleichung **. Der Grund, warum ich es so umgeschrieben habe, ist, dass ich die Strategie $ \ pi $ aus der Formel herausholen konnte, um "ihre Belohnung unabhängig von der von mir gewählten Strategie zu berechnen". Mit anderen Worten, das optimale Verhalten kann nur aus den Spieleinstellungen (Umgebung) berechnet werden. Dies ist der Schlüsselpunkt für das Training des Modells.

Modelllernen

Von hier aus werde ich erklären, wie man das oben gebaute Modell trainiert.

Value Iteration

Berechnen wir anhand der zuvor abgeleiteten Bellman-Gleichung sofort das optimale Verhalten "nur aus der Umgebung". Bei dieser Berechnung wird, wie im ersten Abschnitt erläutert, die Berechnung ab dem Zustand wiederholt, in dem die "letzte Belohnung" erhalten wurde. Diese iterative Berechnung wird als ** Wertiteration ** bezeichnet.

Im Folgenden wird der Status der Wertiteration am Beispiel von Pacman veranschaulicht.

Es ist nach dem Vorbild von Markov Decision Processes and Reinforcement Learning, S. 18-21 modelliert.

Wenn Sie diese Situation aufschreiben, ist dies wie folgt.

Legen Sie eine feste Belohnung fest
Berechnen Sie für jeden Staat die Belohnungen, die durch lebensfähige a verdient werden

\gamma \sum T(s, a, s') U(s')

Berechnen Sie die Gesamtbelohnung $ U (s) $ bei a, was die höchste Belohnung in 1 ergibt.

U(s) = R(s) + \gamma max \sum_{s'} T(s, a, s') U(s') = Bellman Equation!

Kehren Sie zu 1 zurück, bis es konvergiert (bis die Aktualisierungsbreite von $ U (s) $ kleiner wird) und wiederholen Sie die Aktualisierung.

Es wurde nachgewiesen, dass es schließlich zum erwarteten Wert konvergiert.

Auf diese Weise konnte Value Iteration die Belohnungskarte "nur aus der Umgebung" schätzen. In diesem Zustand werden jedoch alle Aktionen, die in allen Situationen ausgeführt werden können, gründlich untersucht, sodass die optimale Aktion abgeleitet werden kann, die jedoch nicht sehr effizient ist. Daher werden wir uns zuerst für eine geeignete Strategie entscheiden, dann nach Belohnungen innerhalb dieses Bereichs suchen und eine Methode zur Aktualisierung in Betracht ziehen. Das ist Policy Iteration.

Policy Iteration

Entscheiden Sie sich in Policy Iteration zunächst für eine geeignete (zufällige) Strategie $ \ pi_0 $. Dann können Sie die "Belohnung aus der Strategie" $ U ^ {\ pi_0} (s) $ berechnen und die darauf basierende Strategie verbessern ($ \ pi_1 $). Mit anderen Worten sind die Schritte wie folgt.

Entscheide dich für eine geeignete Strategie ($ \ pi_0 $)
Berechnen Sie $ U ^ {\ pi_t} (s) $ basierend auf der Strategie
Aktualisieren Sie die Strategie $ \ pi_t $ auf $ \ pi_ {t + 1} . ( \ pi_ {t + 1} = argmax_a \ sum T (s, a, s ') U ^ {\ pi_t} (s') $)
Kehren Sie zu 1 zurück, bis es konvergiert, und wiederholen Sie das Update

Konvergenz bedeutet $ \ pi_ {t + 1} \ approx \ pi_ {t} $, dh wenn die ausgewählte Aktion nahezu unverändert ist. Diese Wiederholung wird als ** Richtlinieniteration ** bezeichnet.

Nun scheint es möglich zu sein, die optimale Strategie mithilfe von Wertiteration und Richtlinieniteration zu berechnen. Wie Sie jedoch aus der Formel ersehen können, muss $ T (s, a, s ') $ für diese Berechnung bekannt sein. Mit anderen Worten, es ist notwendig, das Übergangsziel im Voraus zu klären, wenn in jeder Situation gehandelt wird. Dies ist eine sehr große Einschränkung, und insbesondere wenn eine große Anzahl von Situationen und Maßnahmen ergriffen werden kann, ist es sehr schwierig, alles wie "Dies ist, was hier passiert ..." festzulegen.

Q-Learning, das im nächsten Abschnitt vorgestellt wird, löst dieses Problem. Es wird auch als "modellfreie" Lernmethode bezeichnet, da keine vorherigen Einstellungen für die Umgebung (Modell) erforderlich sind.

Q-learning

Wie lernst du also im Q-Learning ohne Informationen über die Umgebung (Modell)? Die Antwort lautet "versuchen Sie es zuerst". Selbst wenn $ T (s, a, s ') $ unbekannt ist, wird s'klar, wenn Sie einmal a im Zustand s ergreifen, wird s'klar, so dass Sie lernen, indem Sie diesen "Versuch" wiederholen. .. Natürlich braucht es viel Zeit, um so etwas zu tun. In diesem Sinne gibt es den Vorteil, dass es nicht notwendig ist, das Modell im Voraus einzustellen, aber andererseits ist es ein Handicap in Bezug auf die Lernzeit.

Die Formel für "zuerst ausprobieren" lautet wie folgt.

Q(s, a) \approx R(s, a) + \gamma max_{a'} E[Q(s', a')]

$ T (s, a, s ') $ ist verschwunden und ist jetzt der erwartete Wert ($ E [Q (s', a ')] ). Dieser erwartete Wert wird durch Wiederholen des Versuchs verfeinert. Daher werden am Ende die Ausdrücke, die oben fast gleich sind ( \ approx ), als gleiche Ausdrücke festgelegt. Denn die Tatsache, dass die Gleichung gilt, bedeutet, dass der erwartete Wert ( Q (s, a) ) und der erwartete Wert beim tatsächlichen Handeln ( R (s, a) + \ gamma max_ {a '} E [ Dies liegt daran, dass Q (s ', a')] $) gleich ist, was bedeutet, dass wir eine genaue Schätzung der Belohnung haben. Dies ist eine Anleitung zum Abschließen des Lernens.

Die Formel für diesen Lernprozess lautet wie folgt.

Q(s, a) = Q(s, a) + \alpha(\underline{R(s, a) + \gamma max_{a'} E[Q(s', a')]} - \underline{Q(s, a)})

$ \ Alpha $ ist die Lernrate, dh Sie lernen aus der Differenz zwischen dem erwarteten Wert ($ \ ca. $ tatsächliche Belohnung) und dem erwarteten Wert. Diese Differenz (= Fehler) wird als TD-Fehler (TD = zeitliche Differenz) bezeichnet, und die auf TD-Fehlern basierende Lernmethode wird als TD-Lernen bezeichnet. Mit anderen Worten, Q-Learning ist eine Art TD-Lernen.

Die obige Formel wird auch wie folgt angewendet.

Q(s, a) = (1 - \alpha)\underline{Q(s, a)} + \alpha(\underline{R(s, a) + \gamma max_{a'} E[Q(s', a')]})

Es wird ein wenig kompliziert, aber am Ende wird versucht zu klären, "welche Art von Zustand, wie man handelt und welche Art von Belohnung". Diese Belohnungsprognosetabelle wird als Q-Tabelle bezeichnet (siehe Abbildung unten).

Markov Decision Processes and Reinforcement Learning, p39

Von Seite 39 bis Seite 46 des obigen Materials können Sie überprüfen, wie die Q-Tabelle aktualisiert wird, dh wie das Lernen fortschreitet. Bitte beziehen Sie sich darauf (0,9 im Material ist $). \ gamma $, der Abzinsungssatz der Belohnung).

Jetzt können wir $ Q (s, a) $ immer mehr verbessern ... aber es bleibt die Frage, wie man a überhaupt entscheidet. Kurz gesagt, Sie sollten das mit den größten $ Q (s, a) $ auswählen. Wenn Sie dies jedoch tun, wählen Sie weiterhin das "Maximum bekannt" aus, sodass die Belohnung noch unbekannt ist. Es wird die Chancen zerstören, die hohen $ s '$ zu erreichen. Nehmen Sie einen unbekannten Weg, auf dem sich möglicherweise Schätze befinden, oder einen stabilen Weg mit bekannten Belohnungen ... Dies ist ein Kompromiss und wird als Explorations- und Ausbeutungsdilemma bezeichnet. Ich werde.

Es gibt verschiedene Ansätze für dieses Problem, aber die grundlegende Methode ist die ε-gierige Methode. Es ist eine Methode des Abenteuers mit einer Wahrscheinlichkeit von ε und dann gierig, dh basierend auf bekannten Belohnungen. Eine andere Boltzmann-Verteilung ($ P (a | s) = \ frac {e ^ {\ frac {Q (s, a)} {k}}} {\ sum_j e ^ {\ frac {Q (s, a_j)) Es gibt eine Methode mit} {k}}} $), die zufällig ist, wenn $ k $ groß ist, und wenn sie kleiner wird, wird bekannt, dass sie äußerst lohnende Maßnahmen ergreift.

Es wurde bewiesen, dass wenn Sie die Aktion basierend auf der Strategie wiederholen und $ Q (s, a) $ aktualisieren, sie schließlich zum optimalen Wert konvergiert. Ja eines Tages ... Da es jedoch Menschen sind, die eines Tages nicht warten können, wurden verschiedene Versuche unternommen, um herauszufinden, wie das optimale $ Q (s, a) $ angenähert werden kann. Unter diesen hat die Approximation unter Verwendung des neuronalen Netzwerks zu DQN und Deep Q-Learning geführt, die in den letzten Jahren eine bemerkenswerte Genauigkeit erreicht haben.

Deep Q-learning

Die Basis für das Lernen eines neuronalen Netzwerks ist die Fehlerausbreitungsmethode (Back Propagation). Kurz gesagt, es ist eine Methode, das Modell so anzupassen, dass es nahe an der richtigen Antwort liegt, indem der Fehler aus der richtigen Antwort berechnet und in die entgegengesetzte Richtung weitergegeben wird.

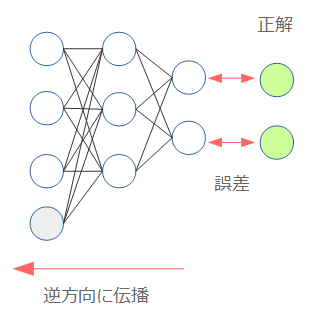Neuronales Netzwerk beginnend mit Chainer

Daher ist die Frage, was der "Fehler" ist, wenn $ Q (s, a) $ mit einem neuronalen Netzwerk angenähert wird. Hier kam der Fehler "TD-Fehler" oben heraus.

Q(s, a) = Q(s, a) + \alpha(R(s, a) + \gamma max_{a'} E[Q(s', a')] - Q(s, a))

Dies war der Unterschied zwischen der erwarteten Belohnung ($ \ ca. $ tatsächliche Belohnung) und der Aussicht. Dies ist wahrscheinlich der Ausgangspunkt für die Definition von Fehlern. Erstens das neuronale Netz $ Q (s, a) $. Das Gewicht des neuronalen Netzes beträgt zu diesem Zeitpunkt $ \ theta $ und $ Q_ \ theta (s, a) $. Dann wird die Definition des Fehlers unter Verwendung des TD-Fehlers in der obigen Formel wie folgt multipliziert.

L_\theta = E[\frac{1}{2} (\underline{R(s, a) + \gamma max_{a'} Q_{\theta_{i-1}}(s', a')} - Q_\theta(s, a))^2]

Das Quadrat ist auf den Fehler zurückzuführen, und $ \ frac {1} {2} $ soll die 2 eliminieren, die bei der Differenzierung erscheint ($ f (x) = x ^ 2 $). Wenn $ f '(x) = 2x $). Wie Sie der Struktur der Formel entnehmen können, ist der unterstrichene Teil (erwarteter Wert) das Lehrerlabel (Ziel) beim überwachten Lernen. Dann ist der Gradient zum Zeitpunkt der Fehlerausbreitung, der durch Differenzieren dieser Gleichung erhalten wird, wie folgt.

\nabla_\theta L(\theta_i) = E[(\underline{R(s, a) + \gamma max Q_{\theta_{i-1}}(s', a')} - Q_{\theta_i}(s, a))\nabla_\theta Q_{\theta_i}(s, a)]

Jetzt können Sie loslegen. Wer hat jedoch ein gutes Verständnis? Sie haben vielleicht gedacht, dass $ Q $ auf der Erwartungswertseite $ Q_ {\ theta_ {i-1}} (s ', a') $ ist. Dies liegt daran, dass der erwartete Wert unter Verwendung des vorherigen $ \ theta $ berechnet wird. Wie oben erwähnt, dient dies als Lehrerbezeichnung für überwachtes Lernen, sodass $ \ theta $ auf der Erwartungswertseite in der Formel enthalten ist, dies ist jedoch nicht Gegenstand der Differenzierung bei der Berechnung des Gradienten. Dies sollte bei der Implementierung berücksichtigt werden.

Jetzt müssen Sie nur noch lernen ... aber in Wirklichkeit funktioniert das Lernen so wie es ist nicht sehr gut. Es ist nur natürlich, dass die Anzahl der Parameter aufgrund des neuronalen Netzes zugenommen hat. Daher wurde ein gewisser Einfallsreichtum beim Lernen entwickelt, und Deep Q-Learning wird nur möglich, wenn dies enthalten ist.

Experience Replay

Die beim Bestärkungslernen angegebenen Daten sind natürlich in chronologischer Reihenfolge fortlaufend. Wenn dies der Fall ist, besteht eine Korrelation zwischen den Daten, sodass das Ziel von Experience Replay darin besteht, sie irgendwie auseinanderzubrechen.

Die Methode besteht darin, zuerst das erlebte Ziel für Status / Aktion / Belohnung / Übergang im Speicher zu speichern und es dann nach dem Zufallsprinzip abzutasten und beim Lernen zu verwenden.

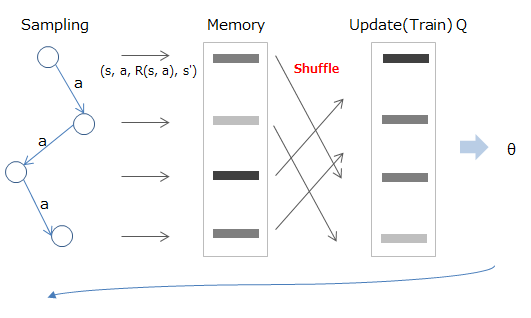
Mathematisch ist es so, als würde man aus dem im Speicher (D) gespeicherten Wert abtasten (roter Teil) und mit dem berechneten erwarteten Wert lernen (blauer Teil).

Deep Reinforcement Learning/David Silver, Google DeepMind, p12

Fixed Target Q-Network

$ Q_ {\ theta_ {i-1}} (s ', a') $ ist im erwarteten Wert enthalten, der das vorherige Gewicht $ \ theta_ {i ist, obwohl es als Lehrerbezeichnung fungiert. Es hängt von -1} $ ab. Daher ändert sich die Bezeichnung als B, und $ \ theta $ wird aktualisiert, obwohl es vor einiger Zeit A war. Es ist ein Zustand der Veränderung am Morgen.

Extrahieren Sie daher wie in Experience Replay oben zunächst einige Beispiele aus den Daten, um einen Mini-Batch zu erstellen. Während des Trainings wird das zur Berechnung des erwarteten Werts verwendete $ \ theta $ festgelegt.

Mathematisch wird durch Festlegen von $ w ^ - $ (rot), das zur Berechnung des erwarteten Werts verwendet wird, wie unten gezeigt, der erwartete Wert (blauer Teil) stabilisiert. Aktualisieren Sie nach Abschluss des Lernens $ w ^ - $ auf $ w $ und fahren Sie mit der Berechnung des nächsten Stapels fort.

Deep Reinforcement Learning/David Silver, Google DeepMind, p13

Belohnungsausschnitt

Dies bedeutet, dass die zu gebende Belohnung fest ist. Wenn sie also positiv ist, ist sie 1 und wenn sie negativ ist, ist sie -1. Daher ist es nicht möglich, die Belohnung zu gewichten (z. B. 10 Punkte! Weil ich das Ziel schnell erreichen konnte), sondern auf Kosten der Erleichterung des weiteren Lernens.

Wie oben beschrieben, umfasst Deep Q-Learning das Verfahren zur Approximation des Q-Learning mit einem neuronalen Netzwerk und (mindestens) die obigen drei Techniken für effizientes Lernen in diesem Fall. Die neuronale Netzwerknäherung hat auch den Vorteil, dass jetzt ein numerischer Vektor als Eingabe für den Zustand s empfangen werden kann. In Spielen wie Block Breaking können auf diese Weise Tricks wie das Vektorisieren des Spielbildschirms und dessen Eingabe und Lernen ausgeführt werden. AlphaGo verwendet dieselbe Methode (wobei das Bild des Bretts als Eingabe verwendet wird). ..

Deep Q-Learning wird derzeit verschiedenen Verbesserungen unterzogen, aber ich denke, dass das Verständnis der oben genannten Inhalte Ihnen hilft, die Forschungstrends zu verstehen.

Trainieren

Bis zu diesem Punkt war der Inhalt theoretisch, also versuchen wir es von hier aus. Es gibt eine Plattform namens Open AI, die verschiedene Lernumgebungen für verbessertes Lernen zusammenfasst. Dieses Mal werde ich dies verwenden, um den Algorithmus tatsächlich zu lernen.

OpenAI Gym OpenAI eröffnet "Training Gym for AI"

Wie Sie hier sehen können, werden verschiedene Lernumgebungen wie Spiele bereitgestellt. Es macht Spaß, es nur anzusehen.

OpenAI Gym environments

Dies ist eigentlich eine Python-Bibliothek, und die Installationsmethode ist auf dem offiziellen GitHub beschrieben.

openai/gym

Die Installation ist im Grunde genommen "pip install gym", kann jedoch nur in der folgenden Umgebung mit der minimalen Konfigurationsinstallation ausgeführt werden.

algorithmic
toy_text
classic_control (benötigt Pyglet zum Zeichnen)

Andere Lernumgebungen erfordern eine zusätzliche Installation. Wenn Sie beispielsweise Atari-Spiele ausführen möchten, müssen Sie zusätzliche Module mit pip install gym [atari] installieren. Möglicherweise müssen Sie etwas anderes als Python installieren, daher können Sie die unter Alles installieren aufgeführten Elemente sicher einschließen. Beachten Sie bei der Verwendung mit Python3 die Beschreibung von Unterstützte Systeme.

Die Verwendung erfolgt wie in Dokument beschrieben, sieht jedoch wie folgt aus.

import gym


env = gym.make('CartPole-v0')  # make your environment!

for i_episode in range(20):
    observation = env.reset()
    for t in range(100):
        env.render()  # render game screen
        action = env.action_space.sample()  # this is random action. replace here to your algorithm!
        observation, reward, done, info = env.step(action)  # get reward and next scene
        if done:
            print("Episode finished after {} timesteps".format(t+1))
            break

Initialisieren Sie die Umgebung mit "env.reset ()" (entspricht dem Zurücksetzen des Spiels).
Bestimmen Sie aus dem beobachteten Zustand (Zustand = "Beobachtung") die Aktion durch einen Algorithmus
Holen Sie sich die Belohnung für die Aktion und den nächsten Status, der durch die Aktion von 'env.step (Aktion)' geändert wird.
done zeigt das Ende der Episode an (mit dem Ergebnis des Spiels). Wenn Sie diesen Punkt erreicht haben, kehren Sie zu 1 zurück und beginnen Sie erneut zu lernen.

Mit "env.monitor" können Sie die Genauigkeit einfach überwachen und Videos aufnehmen. Dieses Ergebnis kann auch auf die OpenAI-Website hochgeladen werden. Wenn Sie ein Kind sind, probieren Sie es aus.

Hier ist der Code, den ich tatsächlich implementiert habe. Da die Ergebnisse in OpenAI Gym hochgeladen werden, können Sie dort auch die Bewertungsergebnisse überprüfen (Algorithmus von icoxfog417).

icoxfog417/chainer_pong

Bei der Implementierung habe ich auf den folgenden Code verwiesen.

Das Lernen nimmt viel Zeit in Anspruch, daher dauert es viel Zeit, um festzustellen, ob es funktioniert (das Erlernen des obigen Kerncodes dauert etwa 3 Tage). Kurz gesagt, wie bei der Bilderkennung ist die Entwicklung ohne GPU schwierig. In diesem Sinne werden GPUs für das moderne maschinelle Lernen unverzichtbar, wenn es nicht nur um das Ausführen von Samples geht.

Es wird jedoch immer einfacher, eine Umgebung wie eine GPU-Instanz von AWS vorzubereiten. Probieren Sie es also aus (obwohl es beim Starten einer Instanz sehr aufregend sein wird).

Das ist alles für die Erklärung. Ich hoffe du kannst von null bis tief tauchen!

[PYTHON] Verbessertes Lernen, um von null bis tief zu lernen

Merkmale des verstärkenden Lernens

Modellierung des verstärkenden Lernens (Markov-Entscheidungsprozess)

Modelllernen

Belohnungsausschnitt

Trainieren

Verweise