introduction

Ceci est le troisième volet de PyTorch Tutoriel officiel après Dernière fois. Cette fois, nous allons procéder avec NEURAL NETWORKS.

Les réseaux de neurones

PyTorch construit un réseau neuronal à l'aide du package torch.nn. La construction du modèle est définie en héritant de nn.Module. nn.Module implémente une couche et une méthode avant qui renvoie la sortie.

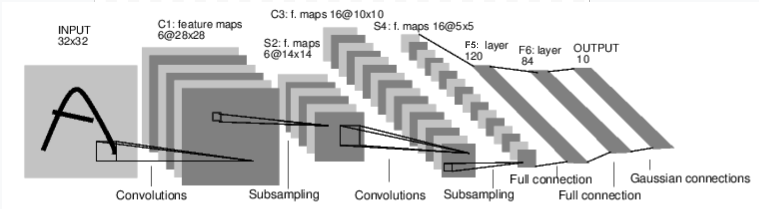
L'image ci-dessus (flux) est un modèle qui juge les nombres dans l'image. Il prend une entrée (INPUT 32 x 32), traverse plusieurs couches et produit le résultat (0 à 9).

Les dimensions de chaque couche changent comme suit. INPUT（32×32）⇒ C1（6×28×28）⇒ S2（6×14×14）⇒ C3（16×10×10）⇒ S4（6×5×5）⇒ F5（120）⇒ F6（84）⇒ OUTPUT（10）

La procédure d'apprentissage du réseau neuronal est la suivante.

--Définir un réseau de neurones --Saisissez le jeu de données

(Traitement des entrées via le réseau) --Calculer la perte --Réflexion du gradient dans les paramètres du réseau (propagation de retour d'erreur) --Mettre à jour les poids du réseau

Regardons chacun.

Définir le réseau

Si vous définissez le réseau dans l'image ci-dessus, ce sera le code suivant.

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
print(net)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

Définissez chaque couche avec init. torch.nn.Module répète le calcul à partir de la couche d'entrée, en calculant les coefficients et les poids et en les passant à la couche suivante. C'est ce qu'on appelle la propagation vers l'avant. torch.nn.Module est un "réseau neuronal à propagation directe". Écrivez ce calcul de propagation avant dans la méthode directe. Le code ci-dessus représente le contenu de l'image dans le code. Ensuite, le résultat du calcul de la propagation vers l'avant peut être obtenu par la méthode Module.parameters ().

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

10
torch.Size([6, 1, 5, 5])

Entrez le jeu de données

[[Autograd: Auto Differentiation](https://pytorch.org/tutorials/beginner/blitz/autograd_tutorial.html#sphx-glr-beginner] sur Dernière fois Comme nous l'avons vu dans -blitz-autograd-tutorial-py), les réseaux de neurones peuvent également calculer des gradients. Le gradient est calculé en entrant l'entrée (32x32) adaptée au réseau neuronal défini comme suit. (Bien qu'il soit un peu différent de l'exemple de code, "requires_grad = True" est ajouté afin que le gradient puisse être calculé.)

input = torch.randn(1, 1, 32, 32, requires_grad=True)
out = net(input)
print(out)

tensor([[-0.0769,  0.1520, -0.0556,  0.0384, -0.0847,  0.1081, -0.0190, -0.0522,
         -0.0523, -0.0007]], grad_fn=<AddmmBackward>)

net.zero_grad()
out.backward(torch.randn(1, 10))

Ci-dessous, vous pouvez afficher le résultat de la rétro-propagation (rétro-propagation).

print(input.grad)

Calculer la perte

La fonction de perte compare la valeur sortie par le réseau avec les données de l'enseignant et évalue la distance entre le résultat de la formation et les données de l'enseignant. Il existe plusieurs fonctions de perte (https://pytorch.org/docs/stable/nn.html#loss-functions) dans le package nn. Une fonction de perte de base est nn.MSELoss. MSELoss est appelé erreur quadratique moyenne, qui met au carré la différence entre le résultat de la formation et les données de l'enseignant et calcule la moyenne.

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

Le résultat de l'entraînement du réseau neuronal est conservé en sortie. Définissez les données de l'enseignant dans la cible. (Cette fois, c'est une valeur aléatoire) Réglez la fonction de perte sur MSELoss. L'erreur entre le résultat de la formation et les données de l'enseignant est calculée pour la perte.

tensor(1.1126, grad_fn=<MseLossBackward>)

Erreur de propagation de retour

Le but de l'apprentissage d'un réseau neuronal est de minimiser les erreurs. Il existe différents algorithmes (algorithmes d'optimisation) pour minimiser, mais ce qu'ils ont en commun, c'est qu'il faut calculer le gradient. Le gradient peut être calculé par la méthode de propagation des erreurs. Avec Pytorch, vous pouvez calculer le gradient simplement en exécutant loss.backward (). Vous pouvez voir le gradient de conv1 avant et après l'appel de loss.backward () dans le code ci-dessous.

net.zero_grad()     #Gradient nul pour tous les paramètres (initialisation)

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([-0.0033,  0.0033,  0.0027,  0.0030,  0.0031, -0.0053])

Mettre à jour les pondérations du réseau

Comme je l'ai mentionné précédemment, l'apprentissage ajuste les paramètres pour minimiser l'erreur (fonction de perte). L'algorithme le plus basique (algorithme d'optimisation) à cet effet est la "descente de gradient stochastique (SGD)". Ce tutoriel n'entre pas dans les détails de Probabilistic Gradient Descent (SGD), mais il peut être implémenté avec un code simple.

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

En plus de la méthode de descente de gradient probabiliste (SGD), il existe divers algorithmes d'optimisation tels que Nesterov-SGD, Adam et RMSProp. torch.optim Divers algorithmes d'optimisation (optimiseurs) sont fournis dans le package.

finalement

C'est tout pour le troisième tutoriel de PyTorch, Neural Networks. J'ai l'impression de comprendre un peu le réseau neuronal de base.

La prochaine fois aimerait continuer avec le quatrième tutoriel "FORMATION D'UN CLASSIFIER".

Histoire

2020/04/22 Première édition publiée 2020/04/29 Lien suivant ajouté

[PYTHON] [Tutoriel PyTorch ③] RÉSEAUX NEURAUX