[PYTHON] [Statistiques] Quelle est la probabilité? Expliquons graphiquement.
En étudiant les statistiques et l'apprentissage automatique, je rencontre le concept de «probabilité». Tout d'abord, j'ai reçu des commentaires que je ne pouvais pas lire, mais c'était "Yudo". C'est "plausible", n'est-ce pas? Chien: chien: pas w Si vous comprenez la fonction de probabilité et la fonction de densité de probabilité, vous pouvez gérer cette probabilité mathématiquement, mais j'aimerais essayer de l'expliquer graphiquement pour une compréhension un peu plus intuitive.
Le code complet est également disponible sur Github (https://github.com/matsuken92/Qiita_Contents/blob/master/General/Likelihood.ipynb).
Prenant une distribution normale comme exemple
La fonction de densité de probabilité de la distribution normale est
f(x)={1 \over \sqrt{2\pi\sigma^{2}}} \exp \left(-{1 \over 2}{(x-\mu)^2 \over \sigma^2} \right)
Peut être exprimé comme. Cela ressemble à ceci dans un graphique.
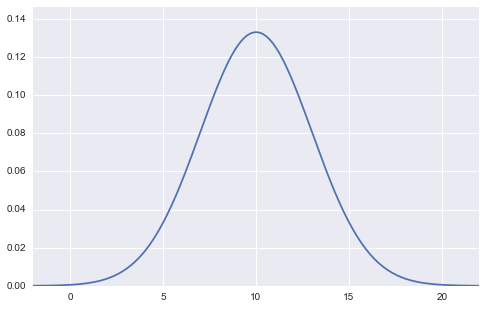
(Figure de distribution normale avec moyenne 10 et écart type 3)
%matplotlib inline
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
import seaborn as sns
import numpy.random as rd
m = 10
s = 3
min_x = m-4*s
max_x = m+4*s
x = np.linspace(min_x, max_x, 201)
y = (1/np.sqrt(2*np.pi*s**2))*np.exp(-0.5*(x-m)**2/s**2)
plt.figure(figsize=(8,5))
plt.xlim(min_x, max_x)
plt.ylim(0,max(y)*1.1)
plt.plot(x,y)
plt.show()
Dans cette figure, les valeurs des deux paramètres, moyenne $ \ mu $ et écart-type $ \ sigma $, sont fixes (dans le cas de la figure ci-dessus, moyenne $ \ mu = 10 $, écart-type $ \ sigma = 3 $). , $ X $ est considéré comme une variable sur l'axe horizontal. L'axe vertical comme sortie est la densité de probabilité $ f (x) $.
Le concept de base de la fonction de vraisemblance est de répondre à la question «Après avoir échantillonné et observé les données, de quels paramètres les données provenaient-elles à l'origine?» Donc, je pense qu'il existe un théorème bayésien inversement probabiliste. (En fait, la vraisemblance est une composante du théorème de Bayes)
(Ci-après, le terme «données» est appelé «échantillon»)
Ici, nous obtenons 10 échantillons ($ {\ bf x} = (x_1, x_2, \ cdots, x_ {10}) $), dont nous savons qu'ils suivent une distribution normale, mais signifient $ \ mu Prenons une situation dans laquelle il n'est pas clair quelles sont les valeurs des deux paramètres $ et l'écart type $ \ sigma $.
plt.figure(figsize=(8,2))
rd.seed(7)
data = rd.normal(10, 3, 10, )
plt.scatter(data, np.zeros_like(data), c="r", s=50)
Considérons d'abord "la distribution simultanée dans laquelle 10 échantillons ont cette valeur". On suppose également que ces 10 échantillons sont iid (distribution identique indépendante: échantillons prélevés indépendamment de la même distribution). Comme il est indépendant, il peut être exprimé comme le produit de chaque densité de probabilité.
P(x_1, x_2,\cdots,x_{10}) = P(x_1)P(x_2)\cdots P(x_{10})
Ce sera. Puisque $ P (x_i) $ était normalement distribué ici,
P(x_1, x_2,\cdots,x_{10}) = f(x_1)f(x_2)\cdots f(x_{10})
C'est aussi bien. Si vous développez cela davantage et écrivez
P(x_1, x_2,\cdots,x_{10}) = \prod_{i=1}^{10} {1 \over \sqrt{2\pi\sigma^{2}}} \exp \left(-{1 \over 2}{(x_i-\mu)^2 \over \sigma^2} \right)
est. Le spécimen $ x_i $ est maintenant à l'intérieur de $ \ exp (\ cdot) $.
Vous disposez désormais d'une fonction de densité de probabilité simultanée pour 10 échantillons. Mais attendez une minute. Maintenant que nous avons l'échantillon comme valeur réalisée, ce n'est plus une valeur probabiliste incertaine. C'est une valeur fixe. Au contraire, je ne connaissais pas les deux paramètres, c'est-à-dire $ \ mu $ et l'écart type $ \ sigma $. Alors, considérez $ x_i $ comme une constante, et changez d'avis pour dire que $ \ mu $ et $ \ sigma $ sont des variables.
La forme de la fonction est exactement la même, et la redéclaration de la variable comme $ \ mu $ et $ \ sigma $ est définie comme vraisemblance
L(\mu, \sigma) = \prod_{i=1}^{10} {1 \over \sqrt{2\pi\sigma^{2}}} \exp \left(-{1 \over 2}{(x_i-\mu)^2 \over \sigma^2} \right)
ça ira. La forme du côté droit ne change pas du tout. Mais le sens a changé.
Je vais comprendre cela comme un graphique.
Rédiger et comprendre des graphiques
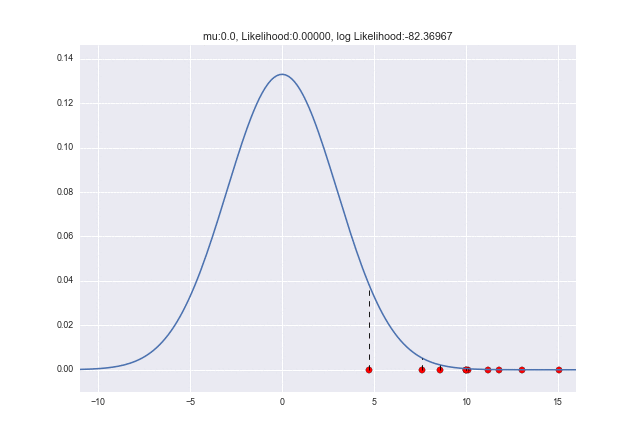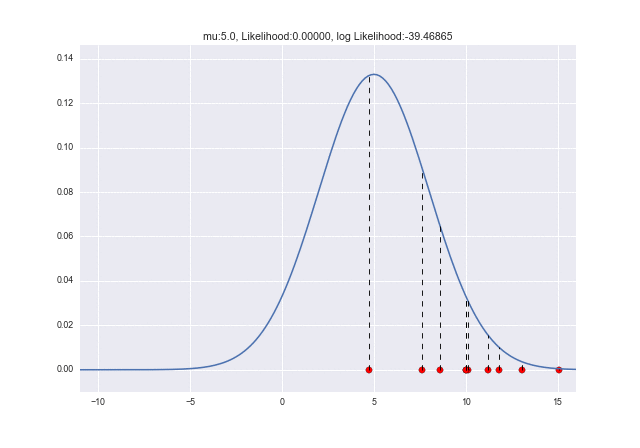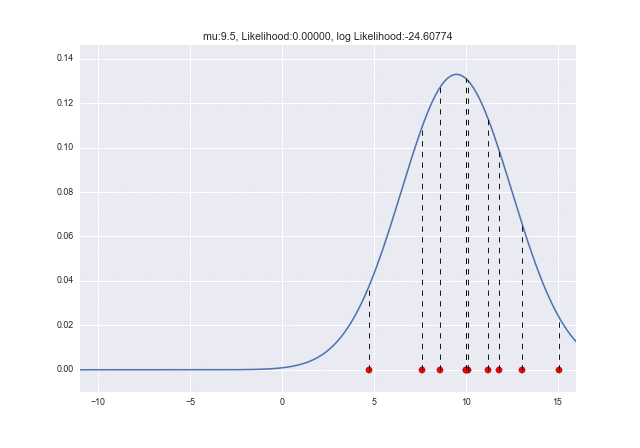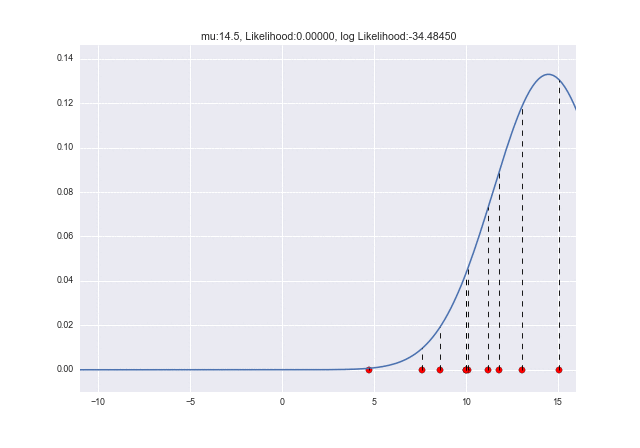
Puisque $ \ mu $ et $ \ sigma $ sont inconnus, si vous pensez que $ \ mu = 0 $ et $ \ sigma = 1 $ et dessinez un graphe,
Ce sera. On a l'impression qu'il est complètement supprimé. À ce stade, la probabilité est également faible.
(Étant donné que la probabilité est calculée en multipliant la probabilité (densité) par le nombre d'échantillons, le nombre entre 0 et 1 sera multiplié plusieurs fois et la multiplication sera un nombre assez petit, presque 0. Dans de nombreux cas, la logarithme est utilisée car elle est facile à ajouter, et dans ce cas, la valeur peut être facilement comprise en regardant la valeur dans le titre du graphique ci-dessus.)
m = 0
s = 1
min_x = m-4*s
max_x = m+4*s
def norm_dens(val):
return (1/np.sqrt(2*np.pi*s**2))*np.exp(-0.5*(val-m)**2/s**2)
x = np.linspace(min_x, max_x, 201)
y = norm_dens(x)
L = np.prod([norm_dens(x_i) for x_i in data])
l = np.log(L)
plt.figure(figsize=(8,5))
plt.xlim(min_x, 16)
plt.ylim(-0.01,max(y)*1.1)
#Dessin de la fonction de densité de la distribution normale
plt.plot(x,y)
#Dessiner des points de données
plt.scatter(data, np.zeros_like(data), c="r", s=50)
for d in data:
plt.plot([d, d], [0, norm_dens(d)], "k--", lw=1)
plt.title("Likelihood:{0:.5f}, log Likelihood:{1:.5f}".format(L, l))
plt.show()
Puisque l'échantillon est situé là où la fonction de densité de probabilité est presque 0, $ L (\ mu, \ sigma) $ a également une probabilité assez faible (vraisemblance logarithmique: environ -568).
Essayons $ \ mu = 5 $ et $ \ sigma = 4 $ cette fois.
(Le code est changé par rapport au précédent uniquement à $ \ mu = 5 $ et $ \ sigma = 4 $)
La ligne pointillée montre la vraisemblance correspondant à chaque échantillon. J'ai l'impression qu'il fait un peu plus chaud qu'avant. Cette fois, la vraisemblance logarithmique a considérablement augmenté jusqu'à environ -20.
Animer et plus intuitif
Utilisons une animation pour voir comment la probabilité change lorsque $ \ mu $ change. Vous pouvez voir que la probabilité du journal est maximale à $ \ mu = 10 $: grin:
from matplotlib import animation as ani
num_frame = 30
min_x = -11
max_x = 21
x = np.linspace(min_x, max_x, 201)
def norm_dens(val, m, s):
return (1/np.sqrt(2*np.pi*s**2))*np.exp(-0.5*(val-m)**2/s**2)
def animate(nframe):
global num_frame
plt.clf()
m = nframe/float(num_frame) * 15
s = 3
y = norm_dens(x, m, s)
L = np.prod([norm_dens(x_i, m, s) for x_i in data])
l = np.log(L)
plt.xlim(min_x, 16)
plt.ylim(-0.01,max(y)*1.1)
#Dessin de la fonction de densité de la distribution normale
plt.plot(x,y)
#Dessiner des points de données
plt.scatter(data, np.zeros_like(data), c="r", s=50)
for d in data:
plt.plot([d, d], [0, norm_dens(d, m, s)], "k--", lw=1)
plt.title("mu:{0}, Likelihood:{1:.5f}, log Likelihood:{2:.5f}".format(m, L, l))
#plt.show()
fig = plt.figure(figsize=(10,7))
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('likelihood.gif', writer='imagemagick', fps=1, dpi=64)
Lorsque $ \ sigma $ change, vous pouvez voir que la probabilité du journal est maximale lorsque $ \ sigma = 2,7 $. Lorsque les données ont été générées à l'origine, c'était $ \ sigma = 3 $, donc il y a une légère erreur, mais les valeurs sont proches les unes des autres: kissing_closed_eyes:
num_frame = 30
min_x = -11
max_x = 21
x = np.linspace(min_x, max_x, 201)
def norm_dens(val, m, s):
return (1/np.sqrt(2*np.pi*s**2))*np.exp(-0.5*(val-m)**2/s**2)
def animate(nframe):
global num_frame
plt.clf()
m = 10
s = nframe/float(num_frame) * 5
y = norm_dens(x, m, s)
L = np.prod([norm_dens(x_i, m, s) for x_i in data])
l = np.log(L)
plt.xlim(min_x, 16)
plt.ylim(-0.01,.6)
#Dessin de la fonction de densité de la distribution normale
plt.plot(x,y)
#Dessiner des points de données
plt.scatter(data, np.zeros_like(data), c="r", s=50)
for d in data:
plt.plot([d, d], [0, norm_dens(d, m, s)], "k--", lw=1)
plt.title("sd:{0:.3f}, Likelihood:{1:.5f}, log Likelihood:{2:.5f}".format(s, L, l))
#plt.show()
fig = plt.figure(figsize=(10,7))
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('likelihood_s.gif', writer='imagemagick', fps=1, dpi=64)
Estimation la plus probable
C'est un graphique du changement de vraisemblance logarithmique lorsque $ \ mu $ est changé. Vous pouvez voir que la valeur de $ \ mu $ sera d'environ 10 lorsque la probabilité est différenciée par $ \ mu $ et mise à 0. C'est l'estimation la plus probable. (En supposant que s est fixe pour le moment)
#Changer m
list_L = []
s = 3
mm = np.linspace(0, 20,300)
for m in mm:
list_L.append(np.prod([norm_dens(x_i, m, s) for x_i in data]))
plt.figure(figsize=(8,5))
plt.xlim(min(mm), max(mm))
plt.plot(xx, (list_L))
plt.title("Likelihood curve")
plt.xlabel("mu")
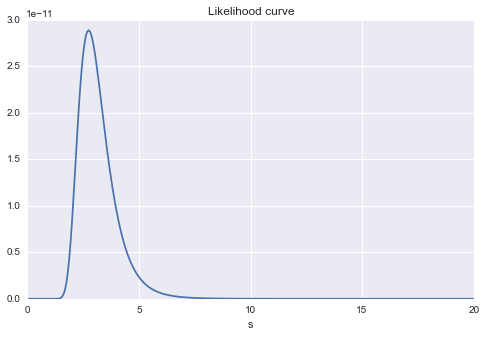
C'est aussi un graphique de changement de probabilité de changement de $ s $. Vous pouvez toujours voir qu'il y aura probablement une valeur maximale autour de $ s = 3 $.
#Changements
list_L = []
m = 10
ss = np.linspace(0, 20,300)
for s in ss:
list_L.append(np.prod([norm_dens(x_i, m, s) for x_i in data]))
plt.figure(figsize=(8,5))
plt.xlim(min(ss), max(ss))
plt.plot(ss, (list_L))
plt.title("Likelihood curve")
plt.xlabel("s")
Enfin, si vous regardez $ \ mu $ et $ \ sigma $ en même temps, $ \ mu $ est un peu plus de 10 et $ \ sigma $ est un peu moins. Vous pouvez voir que la valeur de \ sigma $ est probablement: satisfaite:
#contour
plt.figure(figsize=(8,5))
mu = np.linspace(5, 15, 200)
s = np.linspace(0, 5, 200)
MU, S = np.meshgrid(mu, s)
Z = np.array([(np.prod([norm_dens(x_i, a, b) for x_i in data])) for a, b in zip(MU.flatten(), S.flatten())])
plt.contour(MU, S, Z.reshape(MU.shape), cmap=cm.Blues)
plt.xlabel("mu")
plt.ylabel("s")
Recommended Posts