1. Vue d'ensemble
- Suite à la partie 3 (https://qiita.com/asys/items/9d40172e72dd01caa293), j'étudie sur la base de «l'analyse des séries chronologiques de mesure des données économiques et financières».
- Cette fois à propos du modèle VAR, qui correspond au chapitre 4.
2. Qu'est-ce qu'un modèle VAR?
- Le modèle VAR est une extension du modèle AR multivarié.
- VAR(p) : \mathbb{y}_t=\mathbb{c}+ \Phi _1 \mathbb{y} _{t-1} + \cdots + \Phi _1 \mathbb{y} _{t-p} + \epsilon _t, \quad \epsilon _t \sim W.N.(\Sigma)
- Comme vous pouvez le voir dans la formule, il est caractérisé en ce qu'il ne contient pas d'autres variables en même temps.
*La condition constante est que les valeurs absolues de toutes les solutions des équations caractéristiques AR suivantes soient supérieures à 1.
|\mathbb{I} _n - \Phi _1 z - \cdots - \Phi _p z^p|=0
cependant,\mathbb{I} _nEstn\times nEst une matrice unitaire de.
- Pour l'estimation du modèle, chaque équation peut être estimée individuellement par OLS, et elle peut être estimée par la même méthode que l'estimation du modèle AR.
3. Causalité de Granger
Définition
- La causalité de Granger a été conçue pour que la présence ou l'absence de causalité ne puisse être déterminée qu'à partir des données concernant la relation causale entre les variables.
- Pour $ \ mathbb {x} _t $, l'ensemble des informations disponibles au temps $ t $ est $ \ Omega _t $, $ \ Omega _t $ moins $ \ mathbb {y} _t $ est $ \ Disons tilde {\ Omega} _t $. Lorsque le MSE basé sur $ \ Omega _t $ est plus petit que le MSE pour la prédiction du futur $ \ mathbb {x} $ basé sur $ \ tilde {\ Omega} _t $, $ \ mathbb {y} _t $ Il existe une causalité de Granger de to $ \ mathbb {x} _t $.
- En d'autres termes, il y a causalité lorsque l'information contenue dans $ \ mathbb {y} _t $ améliore la précision de la prédiction lors de la prédiction de $ \ mathbb {x} _t $.
- La causalité de Granger est une condition nécessaire, mais non suffisante, pour que la causalité existe au sens habituel.
Tester
- Soit $ SSR _1 $ la somme résiduelle estimée des carrés en utilisant $ \ Omega _t $, et $ SSR _0 $ la somme résiduelle estimée des carrés en utilisant $ \ tilde {\ Omega} _t $.
- Calculez la statistique $ F $ comme suit: Cependant, $ r $ est le nombre de contraintes requises pour le test.
$ F \ equiv \ frac {\ frac {(SSR_0-SSR_1)} {r}} {\ frac {SSR_1} {(T-np-1)}} $
- $ rF $ est connu pour suivre $ \ chi ^ 2 (r) $ d'une manière graduelle, qui est utilisée pour déterminer la causalité de Granger.
Exemple d'analyse
Les données
- Les données utilisées étaient un ensemble de données appelé FI2010. De là Vous pouvez le télécharger en cliquant sur Accéder à cet ensemble de données librement. Sous Disponibilité des données.
- Bien que les détails soient omis ici, il s'agit d'un ensemble de données d'informations du conseil d'administration sur les bourses. Je l'ai utilisé pour m'y habituer car c'est un ensemble de données que je souhaite personnellement toucher à l'avenir.
- Ici, nous analysons la transition des cours des actions (ci-après dénommée le taux de variation du prix moyen) et le degré de déséquilibre entre les meilleures cotations. En ce qui concerne la meilleure quantité de cotation à un certain moment, s'il y a plus de BID, on pense qu'il y a plus d'acheteurs que de vendeurs, et il est supposé que cela pourrait conduire à de futures augmentations du prix des actions.
<détails> Prétraitement </ summary>
#Lisez les données.
data = pd.read_csv('Train_Dst_Auction_DecPre_CF_1.txt', header=None, delim_whitespace=True)
#Les 4 premières lignes sont les meilleures ASK/Ce sont les données de prix et de quantité pour BID.
#De plus, les 3900 premières colonnes sont les données du premier numéro.
pr = data.iloc[:4,:3900].T
pr.columns = ['ask_p','ask_v','bid_p','bid_v']
#Calculez le prix moyen à partir du meilleur ASK et du meilleur BID.
pr['mid_p'] = (pr['ask_p'] + pr['bid_p']) / 2
#Calculez le taux de variation du prix moyen.
pr['p_chg'] = pr['mid_p'].pct_change()
#Calculez le degré de déséquilibre entre les quantités ASK et BID.
pr['v_imb'] = (pr['ask_v'] / pr['bid_v']).apply(np.log)
pr = pr.dropna()
-
Le graphique des données à utiliser est le suivant.

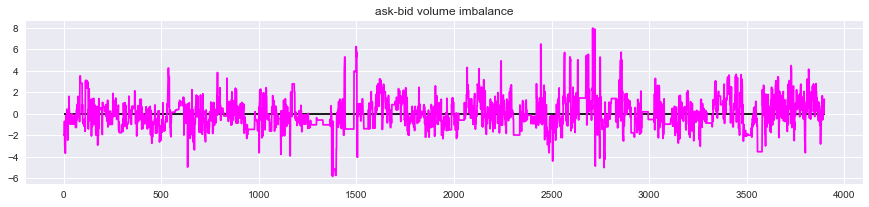
-
Le degré de déséquilibre dans la meilleure quantité de devis est calculé comme suit:
$ \ qquad Imbalance = \ ln \ frac {V_ {ask}} {V_ {bid}} $
, et la valeur est positive. Dans le cas de, la quantité vendue est plus grande, et lorsque la valeur est négative, la quantité d'achat est plus grande.
-
Si la valeur du degré de déséquilibre est positive et que la quantité vendue est plus importante au point précédent, il est facile de vérifier si le cours de l'action baisse à ce stade.
#Cas où il y a plus de vendeurs au point précédent
print('sell > buy ', pr.loc[pr['v_imb'].shift(-1)>1, 'p_chg'].sum())
#Cas où il y avait plus d'acheteurs la fois précédente
print('sell < buy ', pr.loc[pr['v_imb'].shift(-1)<1, 'p_chg'].sum())
# sell > buy -0.0060484707428217765
# sell < buy 0.027729879129729684
En moyenne, s'il y a beaucoup de ventes, le prix moyen baisse, et s'il y a beaucoup d'achats, le prix moyen augmente.
Test de causalité de Granger
- Utilisez les modèles de statistiques familiers à chaque fois.
#Tout d'abord, chargez la bibliothèque et alimentez les données.
from statsmodels.tsa.vector_ar.var_model import VAR
model = VAR(pr[['v_imb','p_chg']].values)
- Ensuite, déterminez l'ordre du modèle. C'est la valeur correspondant à p dans VAR (p). C'est également un coup si vous utilisez la bibliothèque.
model.select_order(10).summary()
|
AIC |
BIC |
FPE |
HQIC |
| 0 |
-15.49 |
-15.48 |
1.880e-07 |
-15.49 |
| 1 |
-16.29 |
-16.28 |
8.405e-08 |
-16.29 |
| 2 |
-16.31 |
-16.30 |
8.217e-08 |
-16.31 |
| 3 |
-16.32 |
-16.30 |
8.173e-08 |
-16.31 |
| 4 |
-16.33* |
-16.30* |
8.101e-08* |
-16.32* |
| 5 |
-16.33 |
-16.29 |
8.103e-08 |
-16.32 |
| 6 |
-16.33 |
-16.29 |
8.108e-08 |
-16.31 |
| 7 |
-16.33 |
-16.28 |
8.112e-08 |
-16.31 |
| 8 |
-16.33 |
-16.27 |
8.116e-08 |
-16.31 |
| 9 |
-16.33 |
-16.27 |
8.111e-08 |
-16.31 |
| 10 |
-16.33 |
-16.26 |
8.120e-08 |
-16.30 |
- Pour le moment, en regardant l'ordre jusqu'à 10, il a été dit que $ p = 4 $ est bon pour tous les quatre critères par défaut, donc l'ordre est décidé à 4.
- Ensuite, regardons la causalité de Granger.
#Créez un modèle avec un ordre de 4.
var_model = model.fit(4)
#Test de causalité de Granger. causer causer=0('v_imb')De utilisé=1('p_chg')Test de causalité à.
Granger = var_model.test_causality(causing=0, caused=1)
Granger.summary()
| Test statistic |
Critical value |
p-value |
df |
| 9.531 |
2.373 |
0.000 |
(4, 7772) |
- En regardant la valeur p, elle est inférieure à 0,05, on peut donc dire que la causalité de Granger existe. Après tout, le degré de déséquilibre du conseil d'administration semble affecter la transition ultérieure des cours des actions.
- Par ailleurs, au contraire, la propriété causale de la transition du cours de l'action au degré de déséquilibre du conseil a été testée comme suit.
Granger = var_model.test_causality(causing=1, caused=0)
Granger.summary()
| Test statistic |
Critical value |
p-value |
df |
| 0.9424 |
2.373 |
0.438 |
(4, 7772) |
- Ici, la valeur P est supérieure à 0,05 et le résultat est qu'aucune causalité n'est observée. Il semble qu'il existe une relation telle qu'une augmentation des ventes due à la hausse des cours des actions, mais la causalité de Granger n'existait pas, probablement parce que le laps de temps analysé était trop court.
4. Fonction de réponse impulsionnelle
Fonction de réponse impulsionnelle non orthogonale
- Dans un modèle VAR général, le changement de $ y_ {i, t + k} $ après k période lorsqu'un choc de 1 unité est donné au terme dérangeant $ \ epsilon_ {jt} $ de $ y_ {jt} $ En tant que fonction.
- IRF_{ij}(k)=\frac{\partial y_{i,t+k}}{\partial \epsilon_{jt}}
- On suppose qu'il n'y a pas de corrélation entre les termes de perturbation, mais en réalité il y a de nombreux cas où il y a une corrélation entre $ \ epsilon_ {it} $ et $ \ epsilon_ {jt} $. Le problème est qu'il n'a pas été bien modélisé.
Fonction de réponse impulsionnelle orthogonale
- Dispersion des termes de perturbation Fonction d'impulsion lorsqu'une matrice de co-dispersion est triangulée, décomposée en termes de perturbation qui ne sont pas corrélés les uns avec les autres, puis un choc de 1 unité est appliqué aux termes de perturbation.
- Dans un modèle VAR général,
$ \ qquad VAR (p): \ mathbb {y} _t = \ mathbb {c} + \ Phi _1 \ mathbb {y} _ {t-1} + \ cdots + \ Phi _1 \ mathbb {y} _ {tp} + \ epsilon _t, \ quad \ epsilon _t \ sim WN (\ Sigma) $
$ A $ est une matrice triangulaire inférieure dont la composante diagonale est égale à 1, $ D Avec $ comme matrice diagonale,
$ \ qquad \ Sigma = ADA '$
et décomposition triangulaire,
$ \ qquad u \ _ t = A ^ {-1} \ epsilon \ _t $
Vous pouvez obtenir le terme de perturbation orthogonale $ u \ _t $ sous la forme>.
- IRF_{ij}(k)=\frac{\partial y_{i,j+k}}{\partial u_{jt}}
- En raison de l'utilisation de la décomposition triangulaire, $ \ epsilon_ {kt} $ est une somme linéaire de $ u_ {1t}, \ cdots, u_ {kt} $. Par conséquent, l'ordre des variables affecte le résultat.
Exemple d'analyse
- Nous continuerons à utiliser les données de la carte utilisées pour la causalité de Granger.
#Créez un modèle avec un ordre de 4.
var_model = model.fit(4)
# k=Calculez les réponses impulsionnelles jusqu'à 10.
IRF = var_model.irf(10)
#Tracez les résultats. orth=Faux signifie non orthogonal.
IRF.plot(orth=False)
plt.show()
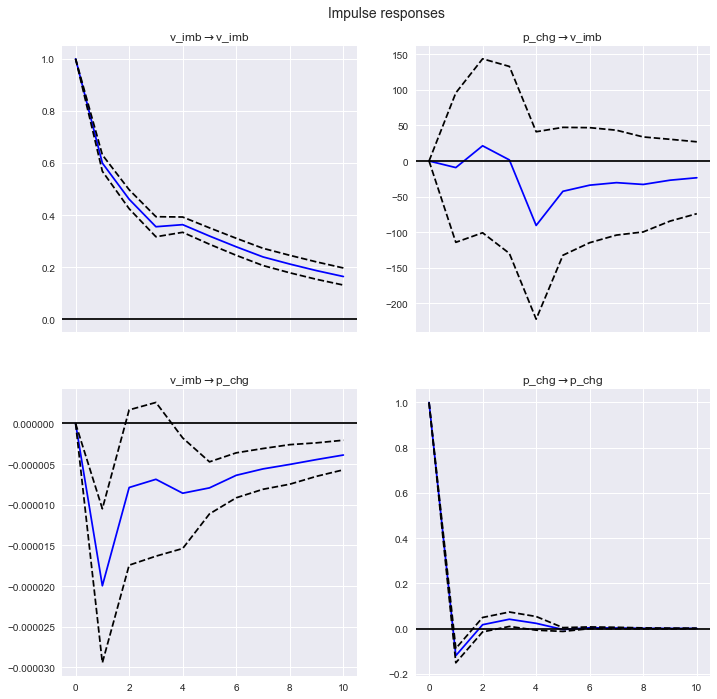
- Ce à quoi je voudrais faire attention est la réponse impulsionnelle de v_imb → p_chg en bas à gauche. Une réaction négative apparaît après une période, puis la réaction diminue progressivement. Une augmentation du déséquilibre d'une unité signifie plus de ventes, ce qui suggère une baisse ultérieure de la performance des stocks.
5. Décomposition distribuée
Définition
- Le rapport du terme de perturbation orthogonale $ u_ {j, t + 1}, \ cdots, u_ {j, t + k} $ de $ y_j $ au MSE de la prédiction de k périodes de $ y_i $ C'est ce qu'on appelle le taux de contribution de dispersion relative (RVC).
*À propos du modèle VAR à n variablesy_iMSE de la prévision future de la période k de\mathbb{u}_{t+1},\cdots,\mathbb{u}\_{t+k}Parce que c'est une somme linéaire de
\qquad \hat{e}\_{i,t+k|t}=\sum\_{h=1}^{k}w\_{1,t+h}^{i}u\_{1,t+h}+\cdots+\sum\_{h=1}^{k}w\_{n,t+h}^{i}u\_{n,t+h}
Puis
\qquad MSE(y\_{i,t+k|t})=\sum\_{l=1}^{n}\sigma\_l^2\sum\_{l=1}^{k}(w\_{l,t+h}^i)^2
\qquad where \quad \sigma\_l^2=E(u\_{lt}^2)
Avec
\qquad RVC\_{ij}(k)=\frac{\sigma\_j^2\sum\_{h=1}^{k}(w\_{j,t+h}^i)^2}{\sum\_{l=1}^{n}\sigma\_l^2\sum\_{h=1}^{k}(w\_{l,t+h}^i)^2}
Cela peut être exprimé par.
Exemple d'analyse
- Continuez à utiliser les données de la carte FI2010.
#Créez un modèle avec un ordre de 4.
var_model = model.fit(4)
# k=Calculez le taux de contribution de dispersion jusqu'à 10.
FEVD = var_model.fevd(10)
#Tracez les résultats.
FEVD.plot()
plt.show()
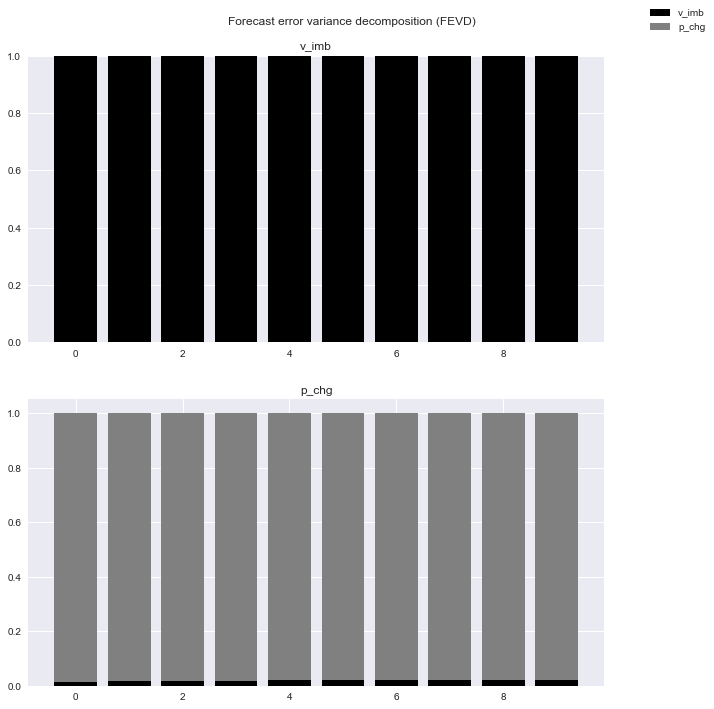
- C'est trop difficile à comprendre, alors regardons des chiffres spécifiques.
FEVD.summary()
| FEVD for v_imb |
v_imb |
p_chg |
| 0 |
1.000000 |
0.000000 |
| 1 |
0.999994 |
0.000006 |
| 2 |
0.999969 |
0.000031 |
| 3 |
0.999971 |
0.000029 |
| 4 |
0.999572 |
0.000428 |
| 5 |
0.999511 |
0.000489 |
| 6 |
0.999478 |
0.000522 |
| 7 |
0.999452 |
0.000548 |
| 8 |
0.999418 |
0.000582 |
| 9 |
0.999397 |
0.000603 |
| FEVD for p_chg |
v_imb |
p_chg |
| 0 |
0.012342 |
0.987658 |
| 1 |
0.018310 |
0.981690 |
| 2 |
0.018871 |
0.981129 |
| 3 |
0.019158 |
0.980842 |
| 4 |
0.019791 |
0.980209 |
| 5 |
0.020477 |
0.979523 |
| 6 |
0.020889 |
0.979111 |
| 7 |
0.021208 |
0.978792 |
| 8 |
0.021472 |
0.978528 |
| 9 |
0.021678 |
0.978322 |
- On peut voir que la contribution de p_chg à la dispersion de v_imb est très faible, ce qui est cohérent en termes de causalité de Granger et de réponse impulsionnelle.
- Au contraire, v_imb contribue pour environ 2% à p_chg. Ce chiffre est également très faible, mais la contribution augmente légèrement à mesure que la période de prévision s'allonge, ce qui suggère qu'il faudra peut-être un certain temps pour que les modifications des conditions du conseil d'administration soient intégrées au cours de l'action.



