Une version mise à jour de cet article est disponible sur mon blog. Voir aussi ici.

introduction

Dans cet article, je vais passer en revue un peu mathématiquement en utilisant la méthode de Newton en référence aux "Mathématiques optimisées" [^ Kanatani] du professeur Kenichi Kanaya. En même temps, voyons à quoi ressemble l'optimisation à l'aide de Python.

Si vous avez des suggestions telles que "C'est mieux ici", je vous serais reconnaissant de bien vouloir nous donner des conseils dans la section commentaires.

1.1 Pour les variables

Par souci de simplicité, commençons par le cas d'une variable. La valeur de la fonction $ f (x) $ autour du point $ \ bar x $ sur l'axe $ x $ peut être développée par Taylor.

f(\bar x + \Delta x) = f(\bar x) + \frac{df}{dx}(\bar x)\Delta x + \frac{1}{2}\frac{d^2f}{dx^2}(\bar x)\Delta x^2 + O(x^3)

Il devient. ($ ~ O (\ cdot) $ est le symbole O de Landau.) Ici, si vous ignorez les termes de $ 3 $ et plus,

f(\bar x + \Delta x) = f(\bar x) + \frac{df}{dx}(\bar x)\Delta x + \frac{1}{2}\frac{d^2f}{dx^2}(\bar x)\Delta x^2

Il devient. Pensez à maximiser cela. Différenciez avec $ \ Delta x $ et définissez $ 0 $ pour obtenir l'équation suivante.

\frac{df}{dx}(\bar x) + \frac{d^2f}{dx^2}(\bar x)\Delta x = 0　\tag{1}

Où $ f ^ {\ prime} (\ bar x) = \ cfrac {df} {dx} (\ bar x), ~~ f ^ {\ prime \ prime} (\ bar x) = \ cfrac {d Si vous définissez ^ 2f} {dx ^ 2} (\ bar x) $ et résolvez pour $ \ Delta x $,

\Delta x = - \frac{f^{\prime}(\bar x)}{f^{\prime\prime}(\bar x)}

Il devient. Ici, puisque $ \ Delta x = x- \ bar x $,

x = \bar x - \frac{f^{\prime}(\bar x)}{f^{\prime\prime}(\bar x)}

peut être obtenu. L'approximation quadratique de $ f (x) $ (approximation par une fonction quadratique) est effectuée pour trouver la valeur de $ x $ qui donne la valeur extrême de la fonction quadratique. C'est le sens du calcul. Ensuite, une approximation quadratique est effectuée autour de la valeur de $ x $ qui donne cette valeur extrême, et la valeur qui devient la valeur extrême est recherchée. L'idée de la méthode de Newton est d'approcher progressivement la valeur extrême de $ f (x) $ en répétant ceci.

En résumé, la procédure est la suivante.

** Méthode de Newton (1) **

Donner la valeur initiale de $ x $
Mettez à jour en tant que $ \ bar x \ leftarrow x $ comme suit. $ x \leftarrow \bar x - \cfrac{f^{\prime}(\bar x)}{f^{\prime\prime}(\bar x)} $ 3. ~|~x - \bar x~| \leq \delta~Vérifiez si c'est le cas. Si faux, revenez à l'étape 2. Si vrai, renvoie x.

1.1 Exemple

Essayons la méthode de Newton avec un exemple simple et analytiquement résoluble dans le livre de référence. Considérez la fonction suivante $ f $.

f(x) = x^3 - 2 x^2 + x + 3

Les dérivés du premier et du second ordre de ceci sont

\frac{df}{dx}(x) = 3x^2 - 4 x + 1\\\\ \frac{d^2f}{dx^2}(x) = 6x - 4

est. Considérons maintenant une approximation quadratique.

f(\bar x + \Delta x) = f(\bar x) + \frac{df}{dx}(\bar x)\Delta x + \frac{d^2f}{dx^2}(\bar x)\Delta x^2

$ \ Delta x = x- \ bar x $, donc

f(x) = f(\bar x) + \frac{df}{dx}(\bar x)(x - \bar x) + \frac{d^2f}{dx^2}(\bar x)(x - \bar x)^2

Il devient. Maintenant, traçons l'approximation quadratique autour de $ f $ et son $ \ bar x = 2 $ sur le même plan!

f = lambda x: x**3 - 2*x**2 + x + 3
d1f = lambda x: 3*x**2 - 4*x + 1
d2f = lambda x: 6*x - 4
f2 = lambda bar_x, x: f(bar_x) + d1f(bar_x)*(x - bar_x) + d2f(bar_x)*(x - bar_x)**2

x = np.linspace(-10, 10, num=100)
plt.plot(x, f(x), label="original")
plt.plot(x, f2(2, x), label="2nd order approximation")
plt.legend()
plt.xlim((-10, 10))

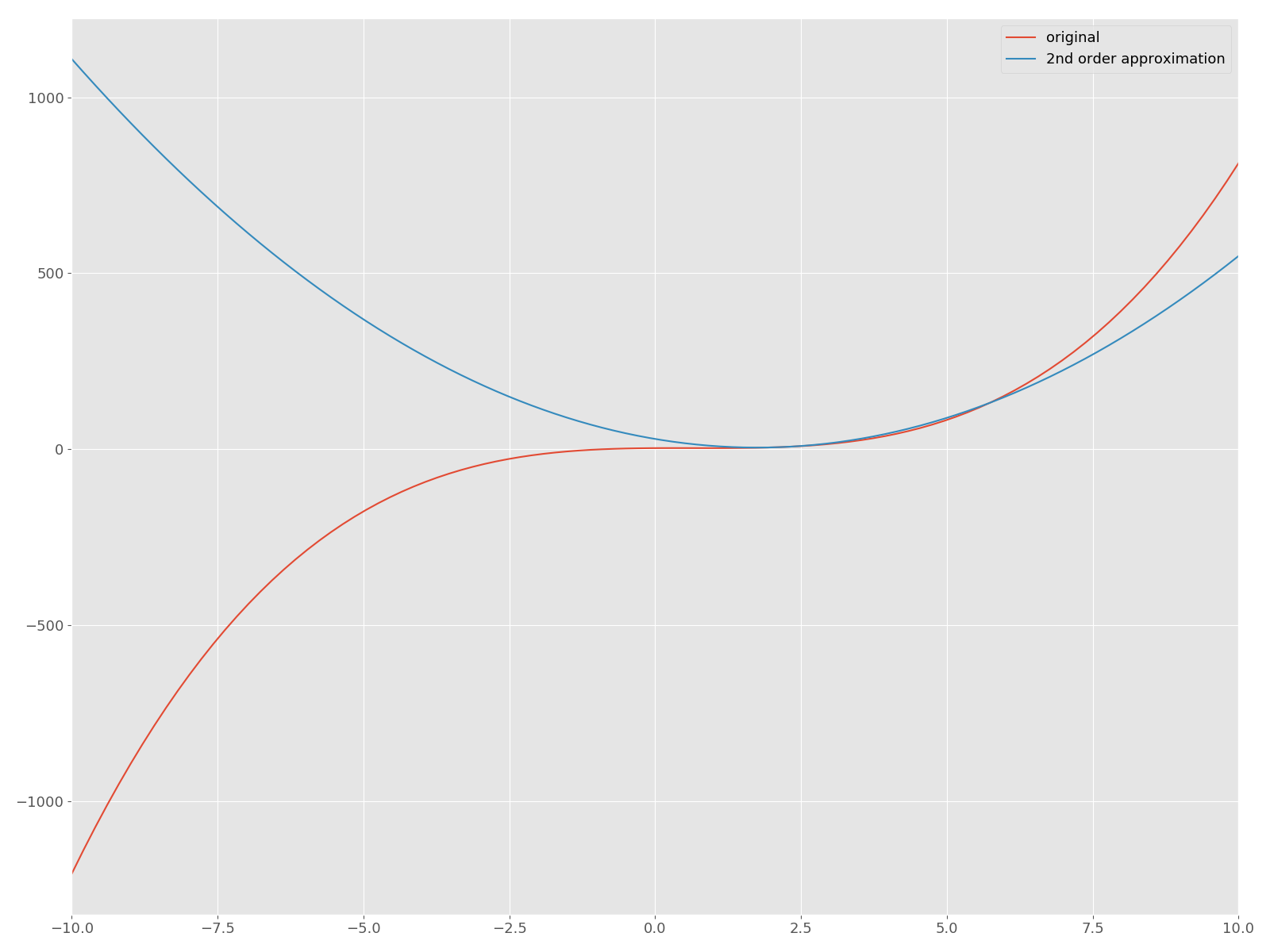
La courbe rouge est la fonction originale $ f $, et la fonction quadratique bleue est la courbe approchée. Maintenant, implémentons la méthode Newton en Python et trouvons une solution qui donne un point d'arrêt. Dans cet article, nous n'oserons pas utiliser des API utiles telles que scipy.optimize.

`newton_1v.py`


class Newton(object):
    def __init__(self, f, d1f, d2f, f2):
        self.f = f
        self.d1f = d1f
        self.d2f = d2f
        self.f2 = f2

    def _update(self, bar_x):
        d1f = self.d1f
        d2f = self.d2f
        return bar_x - d1f(bar_x)/d2f(bar_x)

    def solve(self, init_x, n_iter, tol):
        bar_x = init_x
        for i in range(n_iter):
            x = self._update(bar_x)
            error = abs(x - bar_x)
            print("|Δx| = {0:.2f}, x = {1:.2f}".format(error, x))
            bar_x = x
            if error < tol:
                break
        return x

def _main():
    f = lambda x: x**3 - 2*x**2 + x + 3
    d1f = lambda x: 3*x**2 - 4*x + 1
    d2f = lambda x: 6*x - 4
    f2 = lambda bar_x, x: f(bar_x) + d1f(bar_x)*(x - bar_x) + d2f(bar_x)*(x - bar_x)**2

    newton = Newton(f=f, d1f=d1f, d2f=d2f, f2=f2)
    res = newton.solve(init_x=10, n_iter=100, tol=0.01)
    print("Solution is {0:.2f}".format(res))

if __name__ == "__main__":
    _main()

Si vous faites cela, vous obtiendrez la sortie suivante.

|Δx| = 4.66, x = 5.34
|Δx| = 2.32, x = 3.01
|Δx| = 1.15, x = 1.86
|Δx| = 0.55, x = 1.31
|Δx| = 0.24, x = 1.08
|Δx| = 0.07, x = 1.01
|Δx| = 0.01, x = 1.00
Solution is 1.00

L'intrigue ressemble à ceci: Il diminue de manière monotone vers 0. En fait, la solution obtenue est de 1,00, ce qui est cohérent avec la solution analytique de 1,00 $. Vous pouvez également obtenir 1/3 $ en changeant la valeur initiale. Par exemple, si ʻinit_x` vaut "-10", la solution numérique sera "0,33". Cependant, si le contraire est renvoyé, cela signifie également que la solution obtenue dépend de la valeur initiale.

Le code jusqu'à présent a été téléchargé sur Gist, veuillez donc consulter ici pour plus de détails.

2. Pour plusieurs variables

Ensuite, considérons le cas de plusieurs variables. Fonction au point $ [\ bar x_1, ~ \ cdots, ~ \ bar x_n] $ près du point $ [\ bar x_1 + \ Delta x_1, ~ \ cdots, ~ \ bar x_n + \ Delta x_n] $ (\ bar x_1, ~ \ cdots, ~ \ bar x_n) Lorsque la valeur de $ est étendue par Taylor, $ f(\bar x_1 + \Delta x_1,~\cdots,~\bar x_n + \Delta x_n) = \bar f + \sum^{n}_{i=1} \frac{\partial \bar f}{\partial x\_{i}}\Delta x\_i + \frac{1}{2!} \sum^{n}\_{i,~j=1} \frac{\partial^2 \bar f}{\partial x\_i\partial x\_j}\Delta x\_i \Delta x\_j + \cdots $

Il devient. Je ne dériverai pas cette évolution car elle sort du cadre de cet article, mais je pense qu'il serait bon de se référer à la conférence du professeur Saburo Higuchi [^ Taylor] car elle est très facile à comprendre.

Maintenant, revenons à l'expansion de Taylor. Le $ \ bar f $ utilisé précédemment dans l'expansion de Taylor est la valeur de la fonction $ f $ au point $ [\ bar x_1, ~ \ cdots, ~ \ bar x_n] $. Comme pour le cas à une variable, ignorez les termes après le troisième ordre et définissez $ 0 $ après avoir différencié avec $ \ Delta x_i $.

\frac{\partial \bar f}{\partial x_i} + \sum_{j=1}^{n}\frac{\partial^2 \bar f}{\partial x_i\partial x_j}\Delta x_j = 0

C'est également le cas pour d'autres variables, donc étant donné la matrice de Hesse [^ Hessian]

\nabla \bar f + \boldsymbol{\bar H}\Delta\boldsymbol{x} = \boldsymbol{0}

est. $ \ Nabla $ est un symbole appelé nabla. Par exemple, en prenant une fonction scalaire à deux variables comme exemple, un vecteur avec une différentielle partielle du premier ordre comme élément est créé comme indiqué ci-dessous. C'est ce qu'on appelle un dégradé.

\nabla f(x_0,~x_1) = \begin{bmatrix} \cfrac{\partial \bar f}{\partial x_0} \\\\ \cfrac{\partial \bar f}{\partial x_1} \end{bmatrix}

Par rapport à l'équation (1), vous pouvez voir que le vecteur de gradient correspond à la dérivée du premier ordre et la matrice de Hesse correspond à la dérivée du second ordre. Résolvons ceci pour $ \ boldsymbol {x} $, en faisant attention à $ \ Delta \ boldsymbol {x} = \ boldsymbol {x} - \ boldsymbol {\ bar x} $.

\boldsymbol{x} = \boldsymbol{\bar x} - \boldsymbol{\bar H}^{-1}\nabla \bar f

À partir de ce qui précède, la méthode Newton à ce stade a la procédure suivante.

** Méthode de Newton (2) **

Donnez la valeur initiale de $ \ boldsymbol {x} $
Calculez les valeurs du dégradé $ \ nabla f $ et de la matrice de Hesse $ \ boldsymbol {H} $ en $ \ boldsymbol {\ bar x} $.
Calculez la solution de l'équation linéaire suivante. $ \boldsymbol{H}\Delta\boldsymbol{x} = - \nabla f $
Mise à jour de $ \ boldsymbol {x} . $ \boldsymbol{x}\leftarrow \boldsymbol{x} + \Delta \boldsymbol{x} $$
||\Delta\boldsymbol{x}|| \leq \deltaSi\boldsymbol{x}rends le. Si faux, revenez à l'étape 2.

2.1 Exemple

Maintenant, considérons la fonction suivante, qui est également couverte dans le livre de référence [^ Kanatani].

f(\boldsymbol{x}) = x_{0}^{3} + x_{1}^{3} - 9x_{0}x_{1} + 27

Une approximation quadratique de ceci autour de $ \ boldsymbol {\ bar x} = [\ bar x_0, \ bar x_1] $

f(\boldsymbol{x}) = \bar f + \sum^{1}_{i=0}\frac{\partial \bar f}{\partial x\_i}(x\_i - \bar x\_i) + \frac{1}{2!}\sum^{1}\_{i,~j=0}\frac{\partial^2 \bar f}{\partial x\_i\partial x\_j}(x\_i - \bar x\_i)(x\_j - \bar x\_j)

Et le dégradé $ \ nabla f $ et la matrice de Hesse $ \ boldsymbol {H} $ sont

\nabla f = \begin{bmatrix} \partial \bar f/\partial x_0 \\\\ \partial \bar f/\partial x_1 \end{bmatrix} = \begin{bmatrix} 3 \bar x_0^2 - 9 \bar x_1 \\\\ 3 \bar x_1^2 - 9 \bar x_0 \end{bmatrix}\\\\ \boldsymbol{H}= \begin{bmatrix} \partial^2 \bar f/\partial x_0^2 & \partial^2 \bar f/\partial x_0\partial x_1 \\\\ \partial^2 \bar f/\partial x_1\partial x_0 & \partial^2 \bar f/\partial x_1^2 \end{bmatrix} = \begin{bmatrix} 6\bar x_0 & -9 \\\\ -9 & 6\bar x_1 \end{bmatrix}

Il devient. Implémentons-le en Python.

`newton_mult.py`


import numpy as np
import matplotlib.pyplot as plt

plt.style.use("ggplot")
plt.rcParams["font.size"] = 13
plt.rcParams["figure.figsize"] = 16, 12

class MultiNewton(object):
    def __init__(self, f, dx0_f, dx1_f, grad_f, hesse):
        self.f = f
        self.dx0_f = dx0_f
        self.dx1_f = dx1_f
        self.grad_f = grad_f
        self.hesse = hesse

    def _compute_dx(self, bar_x):
        grad = self.grad_f(bar_x)
        hesse = self.hesse(bar_x)
        dx = np.linalg.solve(hesse, -grad)
        return dx

    def solve(self, init_x, n_iter=100, tol=0.01, step_width=1.0):
        self.hist = np.zeros(n_iter)
        bar_x = init_x
        for i in range(n_iter):
            dx = self._compute_dx(bar_x)
            # update
            x = bar_x + dx*step_width
            print("x = [{0:.2f} {1:.2f}]".format(x[0], x[1]))

            bar_x = x
            norm_dx = np.linalg.norm(dx)
            self.hist[i] += norm_dx
            if norm_dx < tol:
                self.hist = self.hist[:i]
                break
        return x

def _main():
    f = lambda x: x[0]**3 + x[1]**3 - 9*x[0]*x[1] + 27
    dx0_f = lambda x: 3*x[0]**2 - 9*x[1]
    dx1_f = lambda x: 3*x[1]**2 - 9*x[0]
    grad_f = lambda x: np.array([dx0_f(x), dx1_f(x)])
    hesse = lambda x: np.array([[6*x[0], -9],[-9, 6*x[1]]])

    init_x = np.array([10, 8])
    solver = MultiNewton(f, dx0_f, dx1_f, grad_f, hesse)
    res = solver.solve(init_x=init_x, n_iter=100, step_width=1.0)
    print("Solution is x = [{0:.2f} {1:.2f}]".format(res[0], res[1]))

    errors = solver.hist
    epochs = np.arange(0, errors.shape[0])

    plt.plot(epochs, errors)
    plt.tight_layout()
    plt.savefig('error_mult.png')

if __name__ == "__main__":
    _main()

Si vous faites cela, vous obtiendrez la sortie suivante. La solution est $ [3, 3] $ et l'une des solutions analytiques peut être obtenue.

x = [5.76 5.08]
x = [3.84 3.67]
x = [3.14 3.12]
x = [3.01 3.00]
x = [3.00 3.00]
Solution is x = [3.00 3.00]

Enfin, comment va-t-il converger?||\Delta x||Il se termine par un graphique de la transition de.

en conclusion

Jusqu'à présent, nous avons décrit la méthode Newton dans le cas de plusieurs variables, bien que l'exemple commence par une variable et comporte deux variables. Lorsque vous étudiez des algorithmes d'apprentissage automatique, vous trouverez souvent un paramètre qui définit une valeur de référence et donne la valeur minimale (ou maximale) de la fonction. À ce stade, vous utilisez une méthode d'optimisation telle que la méthode Newton. Un rapide coup d'œil aux formules mathématiques peut sembler difficile, mais si vous les lisez à partir de zéro, vous constaterez que si vous avez des connaissances en mathématiques universitaires, vous pouvez les suivre de manière inattendue.

Ces dernières années, vous pouvez essayer immédiatement les algorithmes d'apprentissage automatique en utilisant scicit-learn, etc., mais il est également important de comprendre ce qu'il y a à l'intérieur. C'est la fin de cet article.

(Si vous en avez envie, écrivez la méthode quasi-Newton etc.)

References [^ Kanatani]: Kenichi Kanaya, "Des principes de base des mathématiques optimisées aux méthodes de calcul", Kyoritsu Publishing. [^ Taylor]: Small Integration / Exercise (2006) L09 Taylor Expansion of Multivariate Functions (9.1) Dérivation | Youtube [^ Hessian]: Jugement de valeur extrême de la fonction multivariée et de la matrice de Hesse | Belle histoire de mathématiques au lycée

[PYTHON] Méthode Newton pour l'apprentissage automatique (de 1 variable à plusieurs variables)