[PYTHON] Apprenez à nouveau les bases de Theano
C'est "Theano" qui est un framework de Deep Learning, mais honnêtement c'est assez difficile. En apprentissage, j'ai travaillé en référence au tutoriel original et au commentaire japonais (également en Qiita), mais c'est difficile à comprendre. Ici, nous allons vérifier à nouveau les bases de Theano en déplaçant un petit code. (Mon environnement pour le moment est python 2.7.8, theano 0.7.0.)
Comment utiliser des variables symboliques et partagées
Dans Theano, les soi-disant variables ne sont pas directement manipulées, mais les relations sont décrites par des symboles, qui sont déposés dans le système de traitement, et les entrées / sorties sont effectuées après que le système de traitement les traite si nécessaire. Le fait que la différenciation automatique de l'équation soit incluse dans ce «traitement» est une caractéristique majeure de Theano.
Tout d'abord, utilisons une variable symbolique normale.
import theano
import theano.tensor as T
a = T.dscalar('a')
b = T.dscalar('b')
c = a + 2 * b
f_1 = theano.function([a,b], c)
Si vous entrez jusqu'à ce point et que vous l'exécutez, vous aurez l'impression que le disque dur fait un bruit de cliquetis et génère un fichier intermédiaire. Après cela, la fonction définie est exécutée.
>>> f_1(2,3)
>>> array(8.0)
Jusqu'à présent, comment utiliser les variables symboliques Theano. Extraits de la documentation Theano et listes de différents types de variables.
Theano Variables
| Type de variable | Variables disponibles |
|---|---|
| byte | bscalar, bvector, bmatrix, brow, bcol, btensor3, btensor4 |
| 16-bit integers | wscalar, wvector, wmatrix, wrow, wcol, wtensor3, wtensor4 |
| 32-bit integers | iscalar, ivector, imatrix, irow, icol, itensor3, itensor4 |
| 64-bit integers | lscalar, lvector, lmatrix, lrow, lcol, ltensor3, ltensor4 |
| float | fscalar, fvector, fmatrix, frow, fcol, ftensor3, ftensor4 |
| double | dscalar, dvector, dmatrix, drow, dcol, dtensor3, dtensor4 |
| complex | cscalar, cvector, cmatrix, crow, ccol, ctensor3, ctensor4 |
Comme mentionné ci-dessus, le premier caractère des variables% scalaire et% vecteur indique la longueur en bits de la variable. Si cela est omis, la valeur par défaut "float" et la longueur en bits (type de variable, dtype) seront de type floatX (type qui peut être défini dans la configuration).
Une autre chose à retenir est la ** variable partagée **. Les variables symboliques sont plutôt des variables «fermées» dans Theano, tandis que les variables partagées sont des variables référencées par plusieurs fonctions et utilisées pour des choses qui sont mises à jour à chaque fois, comme les paramètres d'apprentissage. Utilisons cette variable partagée.
w = theano.shared(np.zeros(10), name='w')
print w.get_value()
Comme mentionné ci-dessus, il est défini par theano.shared (valeur initiale, nom du symbole dans Theano). De plus, contrairement aux variables symboliques ordinaires, les variables partagées peuvent être récupérées avec "get_value ()". (À l'inverse, pour récupérer la valeur d'une variable symbolique qui n'est pas une variable partagée, il est nécessaire de préparer une fonction à cet effet.)
>>> print a # Theano Symbol
>>> a # I cannot see it
>>> print b # Theano Symbol
>>> b # I cannot see it...
>>> print w.get_value() # Theano Shared Variable
>>>[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
Lors de la déclaration d'une variable partagée dans le constructeur, il existe une option pour spécifier 'emprunter'.
s_default = theano.shared(np_array) #La valeur par défaut est emprunter=False
s_false = theano.shared(np_array, borrow=False)
s_true = theano.shared(np_array, borrow=True)
Il s'agit d'une option qui ne fait pas de copie lors de la création d'une variable partagée. (L'objet numpy d'origine est détruit.) (Je ne comprends pas encore, alors cliquez ici pour plus de détails [http://deeplearning.net/software/theano/tutorial/aliasing.html#borrowing-when-creating-shared. Voir -variables).)
La fonction de Theano
La partie la plus importante de Theano. Tout d'abord, je citerai quelques styles d'écriture. (Les quatre phrases ne sont pas pertinentes.)
>>> f = theano.function([x], 2*x)
>>> predict = theano.function(inputs=[x], outputs=prediction,
allow_input_downcast=True)
>>> linear_mix = theano.function([A, x, theano.Param(b, default=b_default)], [y, z])
>>> train = theano.function(
inputs=[x,y],
outputs=[prediction, xent],
updates=((w, w - 0.1 * gw), (b, b - 0.1 * gb)),
allow_input_downcast=True)
Comme mentionné ci-dessus, la fonction ano.function () est décrite pendant une longue période en fonction de la façon d'ajouter des options.
Le format le plus court est le suivant.
f = theano.function("contribution", "production")
Ainsi, List et tuple seront utilisés pour plusieurs entrées et sorties. (Il semble que même une variable de type scalaire doit être au format liste pour spécifier l'entrée.) Ce qui suit est une réimpression partielle de l'explication du document.
function.function(inputs, outputs, mode=None, updates=None, givens=None, no_default_updates=False, accept_inplace=False, name=None, rebuild_strict=True, allow_input_downcast=None, profile=None, on_unused_input='raise')
Parameters
- ** params **: valeurs d'entrée (obligatoires, entrées)
- ** sorties **: valeurs de sortie (obligatoire)
- mode
- updates
- givens
- no_default_updates
- name
- rebuild_strict
- allow_input_downcast
- profile
Les ** mises à jour ** sont souvent utilisées pour mettre à jour les paramètres comme cela est fait dans les calculs d'optimisation. Voici un exemple d'utilisation des mises à jour.
a = T.dscalar('a')
w2 = theano.shared(0.0, name='w2')
c = a + 2 * b + w2
f_3 = theano.function([a, b], c, updates=({w2: w2 + 1}))
#Ou f_3 = theano.function([a,b],c, updates=[(w2, w2 + 1)])
for i in range(5):
print f_3(2, 3)
>>>
8.0
9.0
10.0
11.0
12.0
Vous pouvez voir que le contenu des mises à jour est reflété à chaque fois que la fonction est appelée.
** donne ** est utilisé pour attribuer une valeur numérique concrète à une variable. En particulier, il est utilisé lors de l'affectation d'une variable partagée à la fonction ano. (Si vous donnez une variable partagée avec ** entrées **, une erreur se produira.)
w1 = T.dscalar('w1')
c = a + w1 * b
f_2a = theano.function([a, b], c, givens=[(w1, -2.0)])
print f_2a(2, 3)
>>> -4.0 # OK, c=a + w1 *à w1 de b-2.0 est attribué.
#Une erreur se produit lorsqu'une variable partagée est spécifiée dans les entrées.
w2 = theano.shared(-2.0, name='w2') #w2 est une variable partagée
f_2b = theano.function([a, b, w2], c) #Le premier argument est les entrées
---------------------------------------------------------------------------
. . .
TypeError: Cannot use a shared variable (w2) as explicit input. Consider substituting a non-shared variable via the `givens` parameter
** allow_input_downcast ** est utilisé pour assouplir la gestion des types et éviter les erreurs dans les situations où la gestion stricte des types de variables dans Theano provoque une erreur.
Trouvez la valeur minimale (sans utiliser T.grad ())
Je voudrais essayer de trouver la valeur minimale de la fonction avec les fonctions que nous avons vues jusqu'à présent. À titre d'exemple, avec la fonction $ y = (x-1) ^ 4 $, j'ai exécuté un code qui surveille la quantité de changement de y tout en changeant x et effectue un calcul itératif jusqu'à ce que le changement tombe en dessous d'un seuil prédéterminé. (Puisqu'aucune valeur différentielle n'est utilisée, il ne s'agit pas d'une méthode de gradient.)
x_init = -1.0
x = theano.shared(x_init, name='x')
y = T.dscalar('y')
y = (x - 1.) ** 4
#Fonction f_4()Est défini. La valeur d'incrément de x est spécifiée par update.
f_4 = theano.function([], y, updates=({x: x + 0.01}))
# into loop
iter = 1000
y_prev = (x_init -1.1) ** 4
eps = 1.e-6
for i in range(iter):
y_update = f_4() ####En boucle, f_4()appel.
y_delta = np.abs(y_update - y_prev)
if y_delta < eps:
x_min = x.get_value()
break
y_prev = y_update
print 'x_min = ', x_min
>>> x_min = 0.98999995552
Comme prévu, nous avons calculé x_min, ce qui donne la valeur minimale de la fonction $ y = (x-1) ^ 4 $. Je n'ai pas explicitement entré x pour la fonction ano f_4, mais je peux voir que l'option ** updates ** fonctionne correctement.
Essayez d'utiliser la différenciation automatique T.grad ()
Enfin, c'est T.grad () qui est une fonctionnalité de theano.
x = T.dscalar('x')
y = (x - 4) * (x ** 2 * 2+ 6) #Formule différenciée
#Différencier y par rapport à x
gy = T.grad(cost=y, wrt=x)
#Définir une fonction pour trouver le coefficient différentiel,contribution:x,production: gy
f = theano.function(inputs=[x], outputs=gy)
print theano.pp(f.maker.fgraph.outputs[0])
#
print f(0)
print f(1)
print f(2)
>>>
((TensorConstant{1.0} * (((x ** TensorConstant{2}) * TensorConstant{2}) + TensorConstant{6})) + ((((TensorConstant{1.0} * (x - TensorConstant{4})) * TensorConstant{2}) * TensorConstant{2}) * (x ** TensorConstant{1})))
6.0
-4.0
-2.0
Comme mentionné ci-dessus, le résultat de la différenciation de la formule donnée par print theano.pp (...) peut être affiché. De plus, la valeur différentielle y à chaque x (= 0, 1, 2) peut être calculée. Pour le moment, vérifiez les paramètres qui peuvent être spécifiés à partir du document.
theano.gradient.grad(cost, wrt, consider_constant=None, disconnected_inputs='raise', add_names=True, known_grads=None, return_disconnected='zero', null_gradients='raise')
Parameters:
- ** coût **: formule à différencier (obligatoire)
- ** wrt **: Coefficient différentiel (obligatoire)
- consider_constant
- disconnected_inputs
- add_name
- known_grads
- return_disconnected
- null_gradients
cost et wrt sont des paramètres obligatoires.
Mettre en œuvre la descente de gradient
Maintenant que j'ai une meilleure compréhension des pièces nécessaires, je vais mettre en œuvre la méthode de descente de gradient. La fonction cible est la fonction Rosenbrock, qui est (probablement) souvent utilisée dans les algorithmes d'analyse comparative tels que la méthode du gradient.
Fig. Rosenbrock Function
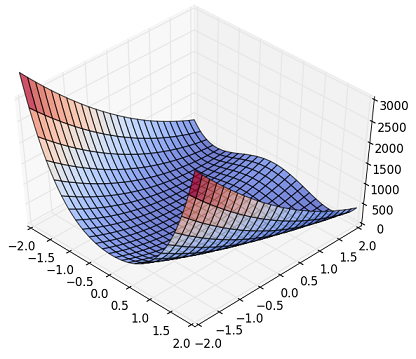
Bien que cela soit difficile à voir sur la figure ci-dessus, il présente une non-linéarité qu'il y a une rainure dans l'anneau et que Z monte brusquement lorsqu'il s'écarte de la partie périphérique. (Il y a une belle figure sur Wikipedia, alors veuillez vous y référer si vous êtes intéressé.)
La formule est la suivante.
f(x, y) = (a - x)^2 + b * (y - x^2)^2
\ \ \ \\usually \ a\ = 1,\ and\ b\ =100
Cette fonction a $ (x, y) = (a, a ^ 2) $ et un minimum global de $ f = 0.0 $. Le code suivant a été créé et exécuté.
import numpy as np
import theano
import theano.tensor as T
# Prep. variables and function
x_init = np.array([2.0, 2.0])
x = theano.shared(x_init, name='x')
a, b = (1., 100.)
# z_rb = (a - x) ** 2 + b * (y - x **2) **2
z_rb = (a - x[0]) ** 2 + b * (x[1] - x[0] **2) **2
dx = T.grad(cost=z_rb, wrt=x)
# Compile
train = theano.function(
inputs=[],
outputs=[z_rb],
updates=[(x, x-0.001 *dx)]
)
# Train
steps = 10000
print '(x,y)_init = (%9.3f, %9.3f)' % (x_init[0], x_init[1])
for i in range(steps):
z_tmp = train()
x_fin = x.get_value()
print '(x,y)_final= (%9.3f, %9.3f)' % (x_fin[0], x_fin[1])
>>>
(x,y)_init = ( 2.000, 2.000)
(x,y)_final= ( 1.008, 1.016)
Les paramètres (x, y) sont résumés dans un vecteur x [] de longueur 2. A partir de la valeur initiale x = [2,0, 2,0], nous avons pu obtenir une valeur proche de la solution théorique (1, 1). La figure ci-dessous trace l'historique de x [](x, y).
Fig. Rosenbrock Function, contour

On voit qu'il est d'abord basculé vers la gauche à partir de (2., 2.) puis tombe dans la rainure annulaire. (Au début, quand j'ai calculé avec les valeurs initiales (3., 3.), ça a divergé à merveille ... Au fait, le code de Numpy + scipy.optimize qui n'utilise pas Theano est la valeur initiale (3. , 3.) a également pu trouver la solution convergente. Il semble qu'elle soit liée à l'algorithme de recherche de solution optimale plutôt qu'à l'utilisation ou non de Theano.)
Si vous pouvez comprendre jusqu'à présent, vous pouvez voir le mouvement du code de référence qui apparaît dans le didacticiel Theano. (En fait, j'ai créé un programme simple pour la régression logistique et je l'ai essayé.) Récemment, "Chainer" est devenu populaire, et le nombre de personnes qui veulent "apprendre le Theano" peut diminuer. Cependant, le premier article sur le Deep Learning à l'étranger traitant de Theano continuera à apparaître, et PyMC3 de la bibliothèque d'implémentation MCMC est également basé sur Theano, donc je pense qu'il est important d'approfondir la compréhension de Theano. Il y a.
Références (site Web)
- Theano Documentation http://deeplearning.net/software/theano/#documentation
- Le mémo de base de [Qiita] Theano http://qiita.com/mokemokechicken/items/3fbf6af714c1f66f99e9
- L'implémentation par Theano de la régression logistique à deux classes, une percée sur l'intelligence artificielle http://aidiary.hatenablog.com/entry/20150519/1432038633
- Documentation sur l'optimisation de SciePy http://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html
- Wikipedia, Rosenbrock function https://en.wikipedia.org/wiki/Rosenbrock_function
Recommended Posts