[Python] Comment faire PCA avec Python

Utilisez ** scikit-learn ** pour faire ** PCA ** en Python. Il existe de nombreuses explications de l'ACP dans le monde, je ne vais donc pas l'expliquer ici, mais simplement expliquer comment l'utiliser.

L'utilisation est simple. n_components est le nombre de composants. Si rien n'est spécifié, ce sera le nombre de dimensions des données. Tout ce que vous avez à faire maintenant est de transmettre les données pour s'adapter.

from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)

Des détails peuvent être trouvés ici [http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html#sklearn.decomposition.PCA.fit_transform).

Création de données de test

J'ai créé les données de test comme ça. Peu importe que la lecture aléatoire soit séparée ou non.

In [10]: x = np.linspace(0.2,1,100)

In [11]: y = 0.8*x + np.random.randn(100)*0.1

In [12]: X = np.vstack([x, y]).T

In [13]: np.random.shuffle(X)

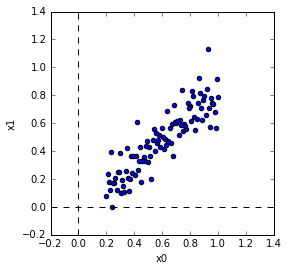
PCA Le PCA devrait être le suivant.

In [14]: from sklearn.decomposition import PCA

In [15]: pca = PCA(n_components=2)

In [16]: pca.fit(X)
Out[16]: PCA(copy=True, n_components=2, whiten=False)

Confirmation des principaux composants

** Les principaux composants ** sont dans components_. Incidemment, vous pouvez voir la ** moyenne ** et la ** matrice de covariance ** avec mean_, get_covariance ().

In [17]: print 'components'
    ...: print pca.components_
    ...: print 'mean'
    ...: print pca.mean_
    ...: print 'covariance'
    ...: print pca.get_covariance()
    ...: 
components
[[ 0.71487492  0.69925235]
 [-0.69925235  0.71487492]]
mean
[ 0.6         0.47190318]
covariance
[[ 0.05441077  0.04603365]
 [ 0.04603365  0.0523763 ]]

Calculons maintenant la ** moyenne ** et la ** matrice de covariance ** par nous-mêmes. La moyenne est la moyenne de chaque composant. La matrice de covariance est un calcul de la covariance. (C'est vrai) Lors du calcul de la covariance, biais = 1 sert à spécifier le dénominateur de la variance et de la covariance. Ici, 1 est spécifié pour diviser par le nombre de données. S'il vaut 0, il est divisé par le nombre de données-1. Vous pouvez voir que les résultats sont les mêmes.

In [22]: mn = np.mean(X,axis=0)

In [23]: z = X - mn

In [24]: cv = np.cov(z[:,0],z[:,1],bias=1)

In [25]: print 'mean'
    ...: print mn
    ...: print 'covariance'
    ...: print cv
    ...: 
mean
[ 0.6         0.47190318]
covariance
[[ 0.05441077  0.04603365]
 [ 0.04603365  0.0523763 ]]

Ensuite, calculez la ** valeur propre ** et le ** vecteur propre ** de la ** matrice de covariance **. Le vecteur propre de la matrice de covariance correspond à la composante principale. Les valeurs propres et les vecteurs propres sont calculés dans numpy.linalg.eig.

W, v = np.linalg.eig(cv)

print 'eigenvector'
print v
print 'eigenvalue'
print W

eigenvector
[[ 0.71487492 -0.69925235]
 [ 0.69925235  0.71487492]]
eigenvalue
[ 0.09943842  0.00734865]

W est la valeur propre et v est le vecteur propre. Ici, le vecteur propre est ** vecteur colonne *. (Doublé verticalement) Autrement dit, v [:, 0] est le premier vecteur propre. Notez que components_ est un ** vecteur de ligne ** (côte à côte). Vous pouvez voir qu'ils correspondent. ( Parfois, la direction est inversée de 180 degrés.)

Multiplions la matrice de covariance par le vecteur propre. Puisque le vecteur propre et l'ACP ont la même composante principale, cela revient à multiplier la matrice de covariance par la composante principale. Puisqu'il s'agit d'un vecteur propre, la direction ne change pas.

In [28]: print cv.dot(v[:,0].reshape(2,1))
    ...: print v[:,0]*W[0]
    ...: print cv.dot(v[:,1].reshape(2,1))
    ...: print v[:,1]*W[1]
[[ 0.07108603]
 [ 0.06953255]]
[ 0.07108603  0.06953255]
[[-0.00513856]
 [ 0.00525337]]
[-0.00513856  0.00525337]

Affichage du vecteur composant principal

Affiche le premier vecteur de composant principal et le deuxième vecteur de composant principal sur les données. Vous pouvez voir que le premier composant principal fait face à la direction de la grande dispersion.

Projection Let's ** Projection ** avec les données comme composant principal. La projection consiste spécifiquement à prendre le produit interne des données et le vecteur composant principal.

In [30]: Xd = pca.transform(X)

Si vous prenez réellement le produit interne des données et le vecteur de composant principal et que vous le vérifiez, vous pouvez voir que c'est la même chose.

In [31]: print pca.components_[0]
    ...: print pca.components_[1]
    ...: print X[0,:]
    ...: print z[0,:]
    ...: print pca.components_[0].dot(z[0,:]), pca.components_[1].dot(z[0,:])
    ...: print Xd[0,:]
[ 0.71487492  0.69925235]
[-0.69925235  0.71487492]
[ 0.57979798  0.47996242]
[-0.02020202  0.00805924]
-0.00880647453855 0.0198876592146
[-0.00880647  0.01988766]

Si vous tracez les données projetées, ce sera comme suit. Si vous regardez la forme tracée, vous pouvez voir que le vecteur du composant principal est tourné vers le nouvel axe.

MNIST Je l'ai essayé avec les données MNIST. MNIST est des données de caractères manuscrites. Les données peuvent être téléchargées depuis ici. Le format des données est également écrit ici. (* Cette fois, j'ai emprunté l'endroit pour lire les données de l'exemple de code de Tensorflow.)

J'ai lu les données et utilisé 256 données du caractère «3». (Parce qu'il y en a beaucoup si vous utilisez tout)

PCA a défini le nombre de composants sur 50 comme indiqué ci-dessous. (50 n'a pas de signification particulière)

In [36]: from sklearn.decomposition import PCA

In [37]: N = 50

In [38]: pca = PCA(n_components=N)

In [39]: pca.fit(X)
Out[39]: PCA(copy=True, n_components=50, whiten=False)

Ce qui suit est une image des principaux composants.

Naturellement, Projection donnera des données à 50 dimensions. Vous pouvez maintenant compresser les dimensions.

In [44]: Xd = pca.transform(X)

In [45]: print X.shape
(256, 784)

In [46]: print Xd.shape
(256, 50)

Revenons à la dimension originale. Utilisez inverse_transform pour revenir en arrière.

In [51]: Xe = pca.inverse_transform(Xd)

In [52]: print Xe.shape
(256, 784)

Ce qui suit est une comparaison de l'original et du résultat de la compression de dimension. La ligne supérieure est l'original et la ligne inférieure est la dimension compressée. Comme le nombre de dimensions était de 50, il est difficile de voir la différence, mais vous pouvez voir que c'est légèrement différent.

Le résultat de la définition du nombre de dimensions sur 3 est le suivant. Le résultat de la compression de dimension a un nombre extrêmement petit de dimensions, donc de petits changements ne peuvent pas être exprimés et tout le monde ressent la même chose.

J'ai collé le code que j'ai utilisé ci-dessous.

code

import numpy as np
import matplotlib.pyplot as plt

# generate data
x = np.linspace(0.2,1,100)
y = 0.8*x + np.random.randn(100)*0.1
X = np.vstack([x, y]).T
np.random.shuffle(X)

# plot data
fig = plt.figure()
axes = fig.add_subplot(111,aspect='equal')
axes.scatter(X[:,0],X[:,1])
axes.set_xlim([-0.2, 1.4])
axes.set_ylim([-0.2, 1.4])
axes.set_xlabel('x0')
axes.set_ylabel('x1')
axes.vlines(0,-0.2,1.4,linestyles='dashed')
axes.hlines(0,-0.2,1.4,linestyles='dashed')

# PCA
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
pca.fit(X)

# print components and mean
print 'components'
print pca.components_
print 'mean'
print pca.mean_
print 'covariance'
print pca.get_covariance()

mn = np.mean(X,axis=0)
z = X - mn
cv = np.cov(z[:,0],z[:,1],bias=1)
print 'mean'
print mn
print 'covariance'
print cv

W, v = np.linalg.eig(cv)
print 'eigenvector'
print v
print 'eigenvalue'
print W

# covariance matrix x eigenvector
print cv.dot(v[:,0].reshape(2,1))
print v[:,0]*W[0]
print cv.dot(v[:,1].reshape(2,1))
print v[:,1]*W[1]
# display 
fig = plt.figure()
axes = fig.add_subplot(111,aspect='equal')
axes.scatter(X[:,0],X[:,1])
axes.set_xlim([-0.2, 1.4])
axes.set_ylim([-0.2, 1.4])
axes.set_xlabel('x0')
axes.set_ylabel('x1')
axes.vlines(0,-0.2,1.4,linestyles='dashed')
axes.hlines(0,-0.2,1.4,linestyles='dashed')
axes.quiver(pca.mean_[0], pca.mean_[1], pca.components_[0,0],pca.components_[0,1], color='red', width=0.01, scale=3)
axes.quiver(pca.mean_[0], pca.mean_[1], pca.components_[1,0],pca.components_[1,1], color='blue', width=0.01, scale=3)

# projection
Xd = pca.transform(X)
print pca.components_[0]
print pca.components_[1]
print X[0,:]
print z[0,:]
print pca.components_[0].dot(z[0,:]), pca.components_[1].dot(z[0,:])
print Xd[0,:]

fig = plt.figure()
axes = fig.add_subplot(111,aspect='equal')
axes.scatter(Xd[:,0],Xd[:,1])
axes.set_xlabel('xd0')
axes.set_ylabel('xd1')
axes.set_xlim([-1.0, 1.0])
axes.set_ylim([-1.,1.0])
axes.vlines(0,-1.0,1.0,linestyles='dashed')
axes.hlines(0,-1.0,1.0,linestyles='dashed')

# MNIST
# generate data  
import numpy as np
import matplotlib.pyplot as plt
import gzip
image_filename = './data/mnist/train-images-idx3-ubyte.gz'
label_filename = './data/mnist/train-labels-idx1-ubyte.gz'
def _read32(bytestream):
  dt = np.dtype(np.uint32).newbyteorder('>')
  return np.frombuffer(bytestream.read(4), dtype=dt)[0]

with gzip.open(image_filename) as bytestream:
    magic = _read32(bytestream)
    num_images = _read32(bytestream)
    rows = _read32(bytestream)
    cols = _read32(bytestream)
    buf = bytestream.read(rows * cols * num_images)
    data = np.frombuffer(buf, dtype=np.uint8)
    data = data.reshape(num_images, rows, cols)

with gzip.open(label_filename) as bytestream:
    magic = _read32(bytestream)
    num_items = _read32(bytestream)
    buf = bytestream.read(num_items)
    labels = np.frombuffer(buf, dtype=np.uint8)

Xall = data[labels == 3, :, :]
X = Xall[0:256,:,:].reshape(256,28*28)
X = X /255.0
# PCA  
from sklearn.decomposition import PCA
N = 3
pca = PCA(n_components=N)
pca.fit(X)

# plot
import matplotlib.pyplot as plt
import matplotlib.cm as cm

cols = 10
rows = int(np.ceil(N/float(cols)))

fig, axes = plt.subplots(ncols=cols, nrows=rows, figsize=(20,10))

for i in range(N):
    r = i // cols
    c = i % cols
    axes[r, c].imshow(pca.components_[i].reshape(28,28),vmin=-0.5,vmax=0.5, cmap = cm.Greys_r)
    axes[r, c].set_title('component %d' % i)
    axes[r, c].get_xaxis().set_visible(False)
    axes[r, c].get_yaxis().set_visible(False)
    
# projection
Xd = pca.transform(X)
print X.shape
print Xd.shape

# inverse
Xe = pca.inverse_transform(Xd)
print Xe.shape


fig, axes = plt.subplots(ncols=10, nrows=2, figsize=(30,4))


for i in range(10):
    axes[0, i].imshow(X[i,:].reshape(28,28),vmin=0.0,vmax=1.0, cmap = cm.Greys_r)
    axes[0, i].set_title('original %d' % i)
    axes[0, i].get_xaxis().set_visible(False)
    axes[0, i].get_yaxis().set_visible(False)
    
    axes[1, i].imshow(Xe[i,:].reshape(28,28),vmin=0.0,vmax=1.0, cmap = cm.Greys_r)
    axes[1, i].set_title('dimension reduction %d' % i)
    axes[1, i].get_xaxis().set_visible(False)
    axes[1, i].get_yaxis().set_visible(False)