[PYTHON] [Français] didacticiel scikit-learn 0.18 Didacticiel d'apprentissage statistique pour le traitement des données scientifiques Apprentissage supervisé: prédire les variables de sortie à partir d'observations en haute dimension
Google traduit http://scikit-learn.org/0.18/tutorial/statistical_inference/supervised_learning.html Table des matières du didacticiel scikit-learn 0.18 Tableau du didacticiel d'apprentissage statistique pour le traitement des données scientifiques Page précédente
Apprentissage supervisé: prédire les variables de sortie à partir d'observations de grande dimension
Problèmes résolus par l'apprentissage supervisé
[Apprendre avec l'enseignant](http://qiita.com/nazoking@github/items/267f2371757516f8c168#1-%E6%95%99%E5%B8%AB%E4%BB%98%E3%81%8D%E5 % AD% A6% E7% BF% 92) est le lien entre les données d'observation «X» et la variable externe «y» (généralement appelée «cible» ou «étiquette») que vous essayez de prédire. C'est apprendre. Souvent, «y» est un tableau unidimensionnel de longueur «n_samples».
Tous les estimateurs supervisés scikit-learn ont une méthode fit (X, y) qui correspond au modèle et un prédire (retourne l'étiquette prédictive y étant donné l'observation non étiquetée X. Implémentez la méthode X) .
Vocabulaire: classification et retour
Si la tâche prédictive consiste à classer les observations dans une série d'étiquettes finies, en d'autres termes, la tâche de «nommer» les objets observés est appelée une tâche de ** classification **. En revanche, si l'objectif est de prédire une variable cible continue, on dit qu'il s'agit d'une tâche de ** régression **.
Lors de la classification avec scikit-learn, y est un vecteur d'entiers ou de chaînes.
Remarque: pour un moyen simple d'implémenter le vocabulaire de base de l'apprentissage automatique utilisé dans scikit-learn, consultez Introduction à l'apprentissage automatique avec le didacticiel scikit-learn. ae16bd4d93464fbfa19b) ".
Malédiction la plus proche et dimensionnelle
Catégoriser les iris:
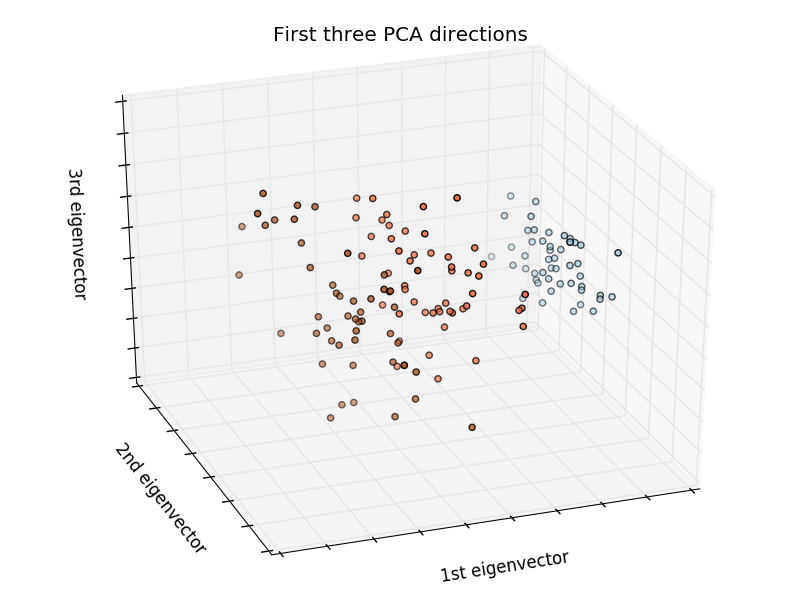
L'ensemble de données d'iris est une tâche de classification qui identifie les types d'iris (Setosa, Versicolour et Virginia) par la longueur et la largeur des pétales et des feuilles.
>>> import numpy as np
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> iris_X = iris.data
>>> iris_y = iris.target
>>> np.unique(iris_y)
array([0, 1, 2])
classificateur de quartier k
Le classificateur le plus simple possible est la méthode la plus proche (https://en.wikipedia.org/wiki/K-nearest_nequart_algorithm). Étant donné un nouvel échantillon «X_test», trouvez des observations avec le vecteur de caractéristiques le plus proche dans l'ensemble d'apprentissage (c'est-à-dire les données utilisées pour entraîner l'estimateur). (Pour plus d'informations sur ce type de classificateur, consultez la section «Nearest Neighbours» du manuel en ligne de Scikit. S'il te plait donne moi).
Ensemble d'entraînement et ensemble de test
Lors de l'expérimentation d'un algorithme d'apprentissage, il est important de ne pas tester les données utilisées pour l'apprentissage afin de pouvoir évaluer les performances de l'estimateur pour les nouvelles données. Pour cette raison, les ensembles de données sont souvent divisés en données d'entraînement et de test.
Exemple de classification KNN (k point le plus proche):
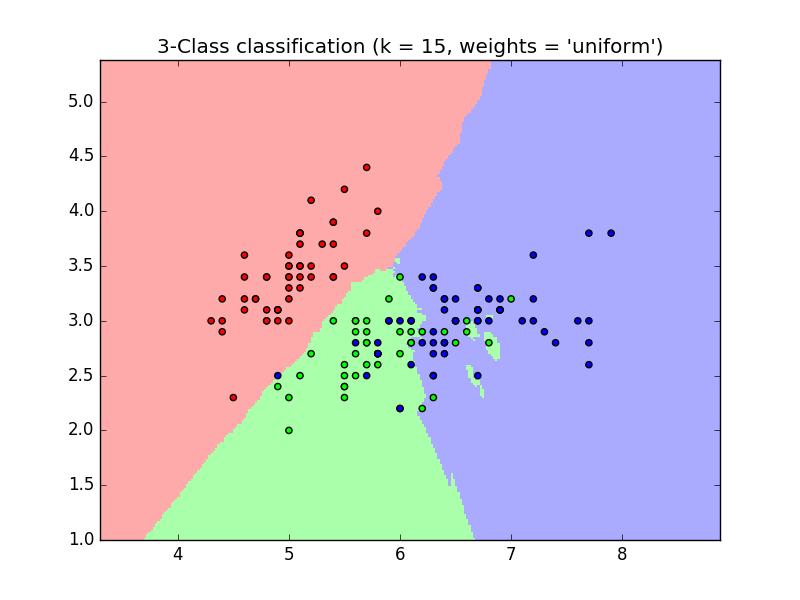
>>> #Divisez les données d'iris en données d'entraînement et données de test
>>> #Remplacement aléatoire qui divise les données de manière aléatoire
>>> np.random.seed(0)
>>> indices = np.random.permutation(len(iris_X))
>>> iris_X_train = iris_X[indices[:-10]]
>>> iris_y_train = iris_y[indices[:-10]]
>>> iris_X_test = iris_X[indices[-10:]]
>>> iris_y_test = iris_y[indices[-10:]]
>>> #Créer et ajuster le classificateur le plus proche
>>> from sklearn.neighbors import KNeighborsClassifier
>>> knn = KNeighborsClassifier()
>>> knn.fit(iris_X_train, iris_y_train)
KNeighborsClassifier(algorithm='auto', leaf_size=30, metric='minkowski',
metric_params=None, n_jobs=1, n_neighbors=5, p=2,
weights='uniform')
>>> knn.predict(iris_X_test)
array([1, 2, 1, 0, 0, 0, 2, 1, 2, 0])
>>> iris_y_test
array([1, 1, 1, 0, 0, 0, 2, 1, 2, 0])
Malédiction dimensionnelle
Pour que l'estimateur soit efficace, la distance entre les points adjacents doit être inférieure à une certaine valeur, $ d $, selon le problème. Dans une dimension, cela nécessite une moyenne de $ n ~ 1 / d $ points. Dans l'exemple de $ k $ voisin ci-dessus, les données sont décrites par une seule quantité d'entités avec une valeur comprise entre 0 et 1, et dans $ n $ observations d'entraînement, les nouvelles données ne dépassent pas 1 $ / n $. .. Par conséquent, si $ 1 / n $ est petit par rapport à l'amplitude de la variation des entités interclasses, la règle de détermination du plus proche voisin est efficace. Si le nombre d'entités est $ p $, vous aurez besoin de $ n à 1 / d ^ p $ points. Disons que vous avez besoin de 10 points dans une dimension. Ici, nous avons besoin de 10 $ ^ p $ points dans la dimension $ p $ pour paver l'espace $ [0, 1] $. À mesure que $ p $ croît, le nombre de points d'entraînement requis pour un bon estimateur augmente de façon exponentielle. Par exemple, si chaque point n'est qu'un nombre (8 octets), un estimateur $ k $ -neighbors valide nécessite plus de données d'apprentissage que la taille actuelle estimée de l'Internet entier (± 1000 exaoctets ou plus). .. Cela s'appelle la malédiction de la dimension (https://en.wikipedia.org/wiki/Curse_of_dimensionality) et est un problème central abordé par l'apprentissage automatique.
Modèle linéaire: de la régression à la parcimonie
Ensemble de données sur le diabète
L'ensemble de données sur le diabète comprend 10 variables physiologiques (âge, sexe, poids, tension artérielle) de 442 patients et des indicateurs de progression de la maladie après 1 an:
>>> diabetes = datasets.load_diabetes()
>>> diabetes_X_train = diabetes.data[:-20]
>>> diabetes_X_test = diabetes.data[-20:]
>>> diabetes_y_train = diabetes.target[:-20]
>>> diabetes_y_test = diabetes.target[-20:]
Le défi actuel est de prédire la progression de la maladie à partir de variables physiologiques.
Régression linéaire
LinearRegression est la forme la plus simple de somme des carrés des résidus de modèle. Ajustez le modèle linéaire à l'ensemble de données en ajustant un ensemble de paramètres pour le rendre aussi petit que possible.
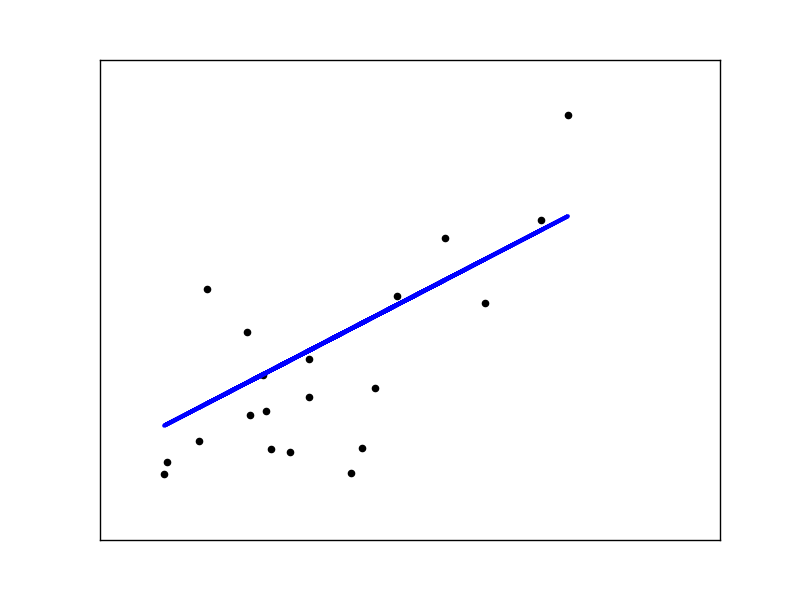
Modèle linéaire: $ y = X \ beta + ε $
- $ X $: Données
- $ y $: variable cible
- $ \ beta $: Coefficient
- $ ε $: Bruit d'observation
>>> from sklearn import linear_model
>>> regr = linear_model.LinearRegression()
>>> regr.fit(diabetes_X_train, diabetes_y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
>>> print(regr.coef_)
[ 0.30349955 -237.63931533 510.53060544 327.73698041 -814.13170937
492.81458798 102.84845219 184.60648906 743.51961675 76.09517222]
>>> #Erreur quadratique moyenne
>>> np.mean((regr.predict(diabetes_X_test)-diabetes_y_test)**2)
2004.56760268...
>>> #Score de variance expliqué: 1 est une prédiction parfaite et 0 signifie qu'il n'y a pas de relation linéaire entre X et y.
>>> regr.score(diabetes_X_test, diabetes_y_test)
0.5850753022690...
Rétrécir
Lorsqu'il y a peu de points de données par dimension, le bruit des valeurs observées provoque une forte dispersion.
X = np.c_[ .5, 1].T
y = [.5, 1]
test = np.c_[ 0, 2].T
regr = linear_model.LinearRegression()
import matplotlib.pyplot as plt
plt.figure()
np.random.seed(0)
for _ in range(6):
this_X = .1*np.random.normal(size=(2, 1)) + X
regr.fit(this_X, y)
plt.plot(test, regr.predict(test))
plt.scatter(this_X, y, s=3)
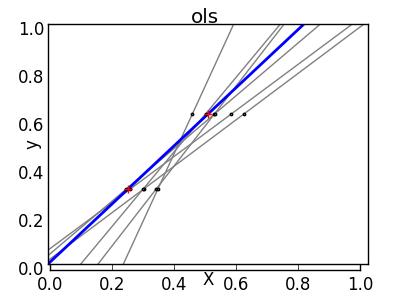
La solution pour l'apprentissage statistique d'ordre supérieur est de réduire le coefficient de régression à zéro. Deux ensembles d'observations choisis au hasard peuvent être décorrélés. Cela s'appelle la régression ridge.
>>> regr = linear_model.Ridge(alpha=.1)
>>> plt.figure()
>>> np.random.seed(0)
>>> for _ in range(6):
... this_X = .1*np.random.normal(size=(2, 1)) + X
... regr.fit(this_X, y)
... plt.plot(test, regr.predict(test))
... plt.scatter(this_X, y, s=3)
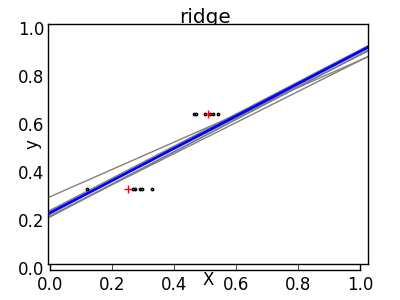
Ceci est un exemple de compromis biais / dispersion. Plus le paramètre "alpha" de la crête est grand, plus le biais est élevé et plus la dispersion est petite. Vous pouvez sélectionner «alpha» pour minimiser les erreurs manquées. Cette fois, nous utilisons l'ensemble de données sur le diabète au lieu des données synthétiques.
>>> alphas = np.logspace(-4, -1, 6)
>>> from __future__ import print_function
>>> print([regr.set_params(alpha=alpha
... ).fit(diabetes_X_train, diabetes_y_train,
... ).score(diabetes_X_test, diabetes_y_test) for alpha in alphas])
[0.5851110683883..., 0.5852073015444..., 0.5854677540698..., 0.5855512036503..., 0.5830717085554..., 0.57058999437...]
** Remarque: ** La capture du bruit qui empêche le modèle d'être généralisé à de nouvelles données avec des paramètres correspondants s'appelle Overfitting (https://en.wikipedia.org/wiki/Overfitting). Le biais introduit par la régression de crête est appelé régularisation (https://en.wikipedia.org/wiki/Regularization_%28machine_learning%29).
Diluité
Montage de la fonction 1 et de la fonction 2 uniquement
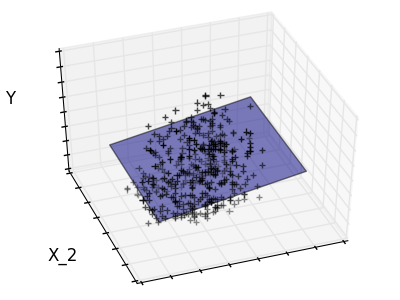
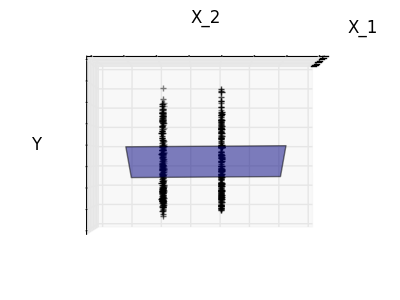
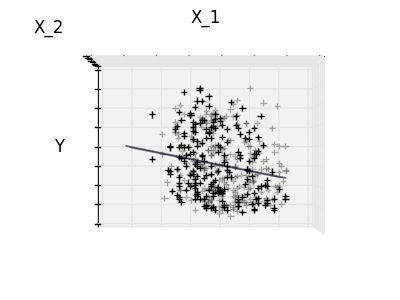
La fonction 2 a un coefficient élevé pour le modèle complet, mais lorsqu'elle est considérée pour la fonction 1, on peut voir qu'elle transmet très peu d'informations sur y. Il serait intéressant de ne sélectionner que les fonctionnalités utiles et de définir 0 pour les fonctionnalités non bénéfiques telles que la fonctionnalité 2 afin d'améliorer la situation en question (c'est-à-dire atténuer la malédiction de la dimension). La régression Ridge réduit leurs contributions, mais ne les met pas à zéro. Une autre approche de pénalité, appelée Lasso (Minimum Absolute Reduction and Selection Operator), vous permet de définir certains coefficients à zéro. Une telle méthode est appelée méthode clairsemée et la rareté peut être considérée comme une application de rasoirs occam.
>>> regr = linear_model.Lasso()
>>> scores = [regr.set_params(alpha=alpha
... ).fit(diabetes_X_train, diabetes_y_train
... ).score(diabetes_X_test, diabetes_y_test)
... for alpha in alphas]
>>> best_alpha = alphas[scores.index(max(scores))]
>>> regr.alpha = best_alpha
>>> regr.fit(diabetes_X_train, diabetes_y_train)
Lasso(alpha=0.025118864315095794, copy_X=True, fit_intercept=True,
max_iter=1000, normalize=False, positive=False, precompute=False,
random_state=None, selection='cyclic', tol=0.0001, warm_start=False)
>>> print(regr.coef_)
[ 0. -212.43764548 517.19478111 313.77959962 -160.8303982 -0.
-187.19554705 69.38229038 508.66011217 71.84239008]
Différents algorithmes pour le même problème
Différents algorithmes peuvent être utilisés pour résoudre le même problème mathématique. Par exemple, l'objet Lasso scikit-learn résout le problème de régression Lasso en utilisant la méthode efficace de descente de coordonnées (https://en.wikipedia.org/wiki/Coordinate_descent) sur de grands ensembles de données. Je vais. Cependant, scikit-learn utilise l'algorithme LARS pour fournir l'objet LassoLars. Faire. Ceci est très efficace pour les problèmes où le vecteur de poids estimé est très rare (problèmes avec très peu d'observations).
Classification
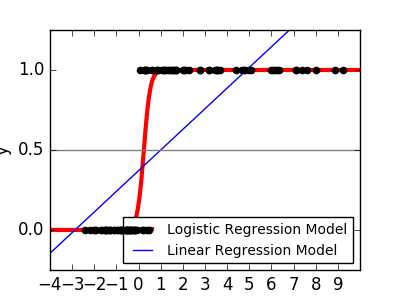
Comme pour la tâche de classification de l'iris, la régression linéaire n'est pas une bonne approche car elle accorde beaucoup de poids aux données éloignées de la frontière de décision. L'approche linéaire consiste à adapter des fonctions sigmoïdes ou logistiques.
y = \textrm{sigmoid}(X\beta - \textrm{offset}) + \epsilon =
\frac{1}{1 + \textrm{exp}(- X\beta + \textrm{offset})} + \epsilon
>>> logistic = linear_model.LogisticRegression(C=1e5)
>>> logistic.fit(iris_X_train, iris_y_train)
LogisticRegression(C=100000.0, class_weight=None, dual=False,
fit_intercept=True, intercept_scaling=1, max_iter=100,
multi_class='ovr', n_jobs=1, penalty='l2', random_state=None,
solver='liblinear', tol=0.0001, verbose=0, warm_start=False)
Cela s'appelle LogisticRegression.
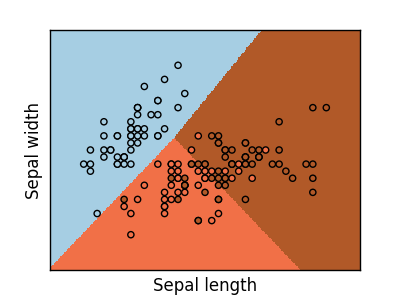
Classification multi-classes
Si vous avez plusieurs classes à prédire, une option courante consiste à insérer un classificateur un-à-tous avant d'utiliser l'heuristique de vote pour prendre la décision finale.
Rétrécissement et minceur dus à la régression logistique
Le paramètre «C» contrôle le degré de normalisation de l'objet LogisticRegression. Des valeurs C plus élevées entraînent une régularisation moindre. penalty =" l2 " donne une contraction (c'est-à-dire un coefficient non clairsemé) et penalty =" l2 " donne une parcimonie.
Exercice
Essayez de classer votre jeu de données numériques en utilisant le voisin le plus proche et un modèle linéaire. Testez ces observations en laissant les 10% restants.
from sklearn import datasets, neighbors, linear_model
digits = datasets.load_digits()
X_digits = digits.data
y_digits = digits.target
Machine à vecteurs de soutien (SVM)
SVM linéaire
Les machines à vecteurs de support appartiennent à la famille des modèles discriminants. Trouvez une combinaison d'échantillons et essayez de construire un plan qui maximise la marge entre les deux classes. La régularisation est définie par le paramètre «C». Une petite valeur pour «C» signifie que la plupart ou toutes les observations autour de la ligne de division sont utilisées pour calculer la marge (et la régularisation). Si la valeur de «C» est grande, cela signifie que la marge est calculée (moins la régularisation) avec la valeur observée proche de la ligne de division.
| SVM non régulier | SVM régularisé(Défaut) |
|---|---|
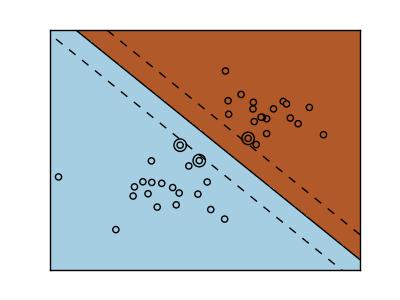 |
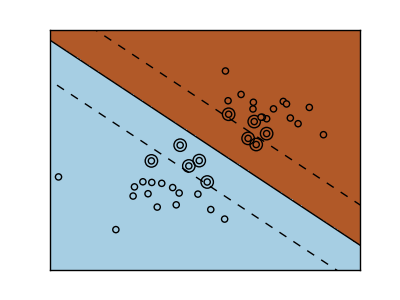 |
--Exemple:
SVM Regression- SVR (Support Vector Regression) -or Classification- [SVC] Il peut être utilisé à l'adresse (http://scikit-learn.org/0.18/modules/generated/sklearn.svm.SVC.html#sklearn.svm.SVC) (Support Vector Classification).
>>> from sklearn import svm
>>> svc = svm.SVC(kernel='linear')
>>> svc.fit(iris_X_train, iris_y_train)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape=None, degree=3, gamma='auto', kernel='linear',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
Utilisation du noyau
Les classes ne peuvent pas toujours être séparées linéairement dans l'espace des fonctions. La solution est de construire un déterminant qui est un polynôme plutôt que linéaire. Ceci est fait en utilisant une astuce du noyau qui peut être considérée pour générer de l'énergie de décision en plaçant le noyau dans l'observation.
Noyau linéaire
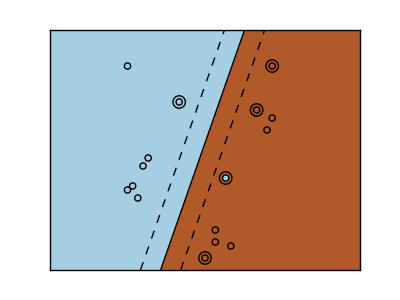
>>> svc = svm.SVC(kernel='linear')
Noyau polygonal
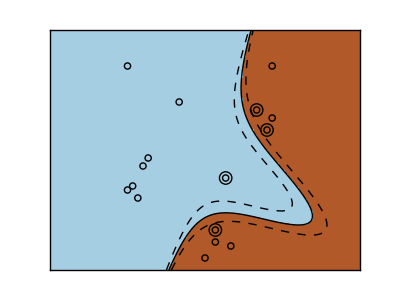
>>> svc = svm.SVC(kernel='poly',
... degree=3)
>>> # degree:Ordre des polygones
Noyau RBF (fonction de base radiale)
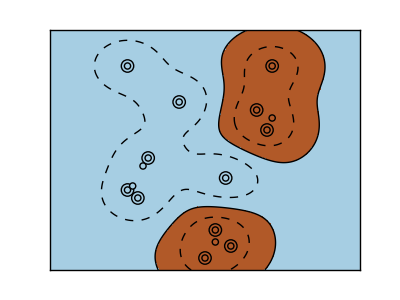
>>> svc = svm.SVC(kernel='rbf')
>>> # gamma:L'inverse de la taille du noyau radial
Exemple interactif
Pour télécharger svm_gui.py, SVM GUI Prière de se référer à. Ajoutez des points de données pour les deux classes avec les boutons droit et gauche pour s'adapter au modèle et modifier les paramètres et les données.

Exercice
Essayez de classer les classes 1 et 2 de l'ensemble de données iris dans un SVM avec les deux premières fonctionnalités. Sur la base de ces observations, nous testerons les performances prédictives, laissant 10% de chaque classe.
ATTENTION: les cours sont commandés et ne laissent pas les 10% restants. Vous ne testez que dans une seule classe. Astuce: vous pouvez obtenir une certaine intuition en utilisant la méthode decision_function sur la grille.
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y != 0, :2]
y = y[y != 0]
Cliquez ici pour obtenir la réponse
Page suivante © 2010 --2016, développeurs scikit-learn (licence BSD).
Recommended Posts