Introduction

A series of optimization algorithm implementations. First, see Overview.

The code can be found on github.

Cuckoo search

Overview

Cucko Search is an algorithm created based on the behavior of cuckoo parasites. Brood parasite is the act of laying eggs in another type of bird's nest and asking the parents of that nest to raise them.

In addition, wild animals including cuckoos are known to move according to a distribution called the Levy distribution called Levy flight when searching for prey.

reference ・ Cuckoo search ・ Introduction to Evolutionary Computation Algorithms Optimal Solutions Derived from Behavioral Sciences of Organisms

algorithm

Eggs are created based on random nests, and another nest is created. The eggs produced at this time are produced according to the Levy distribution.

The nests created will be compared to yet another random nest and will be replaced if desired.

Finally, the nest with a bad rating is discarded and replaced with a new nest.

Algorithm flow

Term correspondence

problem	Cuckoo search
Array of input values	nest
Input value	egg
Evaluation value	巣のEvaluation value

Regarding hyperparameters

Variable name	meaning	Impressions
scaling_rate	Levy distribution scale	The larger it is, the easier it is to move far
levy_rate	Reflection rate of devy flight	The larger it is, the larger the movement by Levy flight
bad_nest_rate	Percentage of bad nests	The higher the value, the more nests can be replaced (search range).

Creating a nest

Create new nests from randomly selected nests according to the Levy distribution.

x^{new}_i = x^{r}_i + \alpha s

$ s $ is a random number (Lévy flight) according to the Levy distribution, and $ \ alpha $ is the reflection rate of Levy flight. Generating this nest is all about cuckoo search, but Levy flight is a bit tricky.

The Levy distribution is below.

f(x; \mu, c) = \sqrt{ \frac{c}{2 \pi} } \frac{ \exp^{\frac{-c}{2(x - \mu)}} }{ (x - \mu)^{\frac{2}{3}}}

import math
def levy(x, u=0, c=1):
    if x == 0:
        return 0
    t = math.exp((-c/(2 * (x-u))))
    t /= (x-u) ** (3/2)
    return math.sqrt(c/(2*math.pi)) * t

We need to generate random numbers according to this Levy distribution. Random numbers according to the Levy distribution are calculated by the Mantegna algorithm.

s = \frac{u}{|v|^{\frac{1}{\beta}}}

Where $ \ beta $ is a scaling index that takes a real number between 0 and 2. $ u $ is a random number that follows a normal distribution with mean 0, variance $ \ sigma ^ 2 $, $ v $ is a random number that follows a standard normal distribution.

$ \ sigma $ can be calculated by the following formula.

\sigma = \Biggl( \frac{ \Gamma(1+\beta) \sin(\frac{\pi \beta}{2}) }{ \Gamma(\frac{1+\beta}{2}) \beta 2^{\frac{(\beta-1)}{2}} } \Biggr)^{\frac{1}{\beta}}

$ \ Gamma $ represents the gamma function.

\Gamma(x) = \int_{0}^{\infty} t^{x-1}e^{-t} dt

Normal distribution random numbers

It's a normally distributed random number, but you can easily get it with the following using python's numpy library.

import numpy as np
np.random.randn()  #Generate uniform random numbers with standard normal distribution
np.random.normal(0, sigma)  #Mean 0, variance sigma^Random numbers that follow a normal distribution of 2

However, I am thinking of implementing it in other languages (mainly lua), so I will write a method that does not use the library.

Random numbers with a standard normal distribution can be obtained by the Box-Muller method.

z = \sqrt{-2 \log{X}} \cos{2\pi Y}

Where X and Y are uniform random numbers that are independent of each other. It is as follows in python.

import math
def random_normal():
    r1 = random.random()
    r2 = random.random()
    return math.sqrt(-2.0 * math.log(r1)) * math.cos(2*math.pi*r2)

Gamma function

The gamma function can also be easily obtained by using math.

import math
math.gamma(x)

If I don't use it, I used the code of Site here. (The code is described in the whole code)

Regarding the Levy distribution

It is a graph of the Levy distribution.

It is a Levy distribution, but as you can see, the range is 0 to ∞. This is a bit of a bottleneck when spawning eggs.

For example, in the case of OneMax problem, the range is only 0 to 1. It is undecided what to do with values greater than or equal to 1 generated by the Levy distribution for this problem. Here, for example, if a value of 1 or more is set to 1, the generated random numbers will not follow the Levy distribution. (The probability of generating 1 will increase)

How about this? I'm not sure how to solve it, so I'm leaving it for now.

Whole code

import math
import random

import numpy as np


############################################
#Calculation of Γ (x) (gamma function, approximation formula)
#      ier : =0 : normal
#            =-1 : x=-n (n=0,1,2,･ ･ ･)
#      return :result
#      coded by Y.Suganuma
# https://www.sist.ac.jp/~suganuma/programming/9-sho/prob/gamma/gamma.htm
############################################
def gamma(x):
    if x <= 0:
        raise ValueError("math domain error")

    ier = 0

    if x > 5.0 :
        v = 1.0 / x
        s = ((((((-0.000592166437354 * v + 0.0000697281375837) * v + 0.00078403922172) * v - 0.000229472093621) * v - 0.00268132716049) * v + 0.00347222222222) * v + 0.0833333333333) * v + 1.0
        g = 2.506628274631001 * math.exp(-x) * pow(x,x-0.5) * s

    else:

        err = 1.0e-20
        w   = x
        t   = 1.0

        if x < 1.5 :

            if x < err :
                k = int(x)
                y = float(k) - x
                if abs(y) < err or abs(1.0-y) < err :
                    ier = -1

            if ier == 0 :
                while w < 1.5 :
                    t /= w
                    w += 1.0

        else :
            if w > 2.5 :
                while w > 2.5 :
                    w -= 1.0
                    t *= w

        w -= 2.0
        g  = (((((((0.0021385778 * w - 0.0034961289) * w + 0.0122995771) * w - 0.00012513767) * w + 0.0740648982) * w + 0.0815652323) * w + 0.411849671) * w + 0.422784604) * w + 0.999999926
        g *= t

    return g


def random_normal():
    """
Random numbers with normal distribution
Box-Muller method
    """
    r1 = random.random()
    r2 = random.random()
    return math.sqrt(-2.0 * math.log(r1)) * math.cos(2*math.pi*r2)


def mantegna(beta):
    """
mantegna algorithm
    """
    #beta:  0.0 - 2.0
    if beta < 0.005:
        #OverflowError if too low: (34, 'Result too large')
        beta = 0.005
    # siguma
    t = gamma(1+beta) * math.sin(math.pi*beta/2)
    t = t/( gamma((1+beta)/2) * beta * 2**((beta-1)/2) )
    siguma = t**(1/beta)

    u = random_normal()*siguma  #Mean 0 variance siguma^Random numbers that follow a normal distribution of 2
    v = random_normal()  #Random numbers that follow a standard normal distribution

    s = (abs(v)**(1/beta))
    if s < 0.0001:
        #ValueError if too low: supplied range of [-inf, inf] is not finite
        s = 0.0001
    s = u / s
    return s


class Cuckoo():
    def __init__(self, 
        nest_max,
        scaling_rate=1.0,
        levy_rate=1.0,
        bad_nest_rate=0.1
    ):
        self.nest_max = nest_max
        self.scaling_rate = scaling_rate
        self.levy_rate = levy_rate

        #Calculate the number of bad nests from the percentage of bad nests
        self.bad_nest_num = int(nest_max * bad_nest_rate + 0.5)
        if self.bad_nest_num > nest_max-1:
            self.bad_nest_num = nest_max-1
        if self.bad_nest_num < 0:
            self.bad_nest_num = 0

    def init(self, problem):
        self.problem = problem

        self.nests = []
        for _ in range(self.nest_max):
            self.nests.append(problem.create())
    
    def step(self):
        #Randomly select a nest
        r = random.randint(0, self.nest_max-1)  # a<=x<=b

        #Create a new nest
        arr = self.nests[r].getArray()

        for i in range(len(arr)):

            #Make eggs with Levi fly
            arr[i] = arr[i] + self.levy_rate * mantegna(self.scaling_rate)

        new_nest = self.problem.create(arr)

        #Change if you like compared to a random nest
        r = random.randint(0, self.nest_max-1)  # a<=x<=b
        if self.nests[r].getScore() < new_nest.getScore():
            self.nests[r] = new_nest

        #Erase the bad nest and make a new one
        self.nests.sort(key=lambda x:x.getScore())
        for i in range(self.bad_nest_num):
            self.nests[i] = self.problem.create()

Cuckoo search (ε-greedy)

This is the original of this article. (Maybe if you look for it?) Cuckoo search is a very simple algorithm, but implementing Levy flight is very tricky.

So I replaced Levy Flight with ε-greedy. Replacing it with ε-greedy made it a lot easier to implement.

I feel that even with ε-greedy, the accuracy is reasonable.

Whole code

import math
import random

class Cuckoo_greedy():
    def __init__(self, 
        nest_max,
        epsilon=0.1, 
        bad_nest_rate=0.1
    ):
        self.nest_max = nest_max
        self.epsilon = epsilon

        #Calculate the number of bad nests from the percentage of bad nests
        self.bad_nest_num = int(nest_max * bad_nest_rate + 0.5)
        if self.bad_nest_num > nest_max-1:
            self.bad_nest_num = nest_max-1
        if self.bad_nest_num < 0:
            self.bad_nest_num = 0

    def init(self, problem):
        self.problem = problem

        self.nests = []
        for _ in range(self.nest_max):
            self.nests.append(problem.create())
    
    def step(self):
        #Randomly select a nest
        r = random.randint(0, self.nest_max-1)  # a<=x<=b

        #Create a new nest
        arr = self.nests[r].getArray()

        for i in range(len(arr)):

            # ε-Create a new egg with greedy
            if random.random() < self.epsilon:
                arr[i] = self.problem.randomVal()

        new_nest = self.problem.create(arr)

        #Change if you like compared to a random nest
        r = random.randint(0, self.nest_max-1)  # a<=x<=b
        if self.nests[r].getScore() < new_nest.getScore():
            self.nests[r] = new_nest

        #Erase the bad nest and make a new one
        self.nests.sort(key=lambda x:x.getScore())
        for i in range(self.bad_nest_num):
            self.nests[i] = self.problem.create()

Hyperparameter example

It is the result of optimizing hyperparameters with optuna for each problem. A single optimization attempt yields results with a search time of 2 seconds. I did this 100 times and asked optuna to find the best hyperparameters.

Cuckoo search

problem	bad_nest_rate	levy_rate	nest_max	scaling_rate
EightQueen	0.09501642206708413	0.9797131483689493	14	1.9939515457735189
function_Ackley	0.0006558326608885681	0.3538825414958845	4	0.9448539685962172
function_Griewank	0.23551408245457767	0.30150681160121073	2	0.9029863706820189
function_Michalewicz	0.00438839398648697	0.0004796264527609298	2	1.5288609934193742
function_Rastrigin	0.13347040982335695	0.031401149135082206	7	1.6949622109706082
function_Schwefel	0.0003926596935418525	0.02640034426449156	4	0.5809451877075759
function_StyblinskiTang	0.08462936367613791	0.0633939067767827	5	1.7236388666366773
LifeGame	0.8819375718376719	0.015175414454036936	33	1.3899842408715666
OneMax	0.89872646833605	0.1261650035421213	17	0.04906594355889626
TSP	0.024559598255857823	0.008225444982304852	4	1.8452535160497248

Cuckoo search (ε-greedy)

problem	bad_nest_rate	epsilon	nest_max
EightQueen	0.004374125594794304	0.03687227169502155	7
function_Ackley	0.5782260075661492	0.031195954391595435	2
function_Griewank	0.23314007403872794	0.05206930732996057	2
function_Michalewicz	0.11845570554906226	0.02242832420874199	3
function_Rastrigin	0.009725819291390304	0.025727770986639094	3
function_Schwefel	0.22978641596753258	0.048159183280607774	2
function_StyblinskiTang	0.14184473157004032	0.01965829867603547	2
LifeGame	0.7358005558643367	0.9115290938258255	39
OneMax	0.0016700608620328905	0.006003869128710593	2
TSP	0.00023997215188062415	0.030790166824531992	29

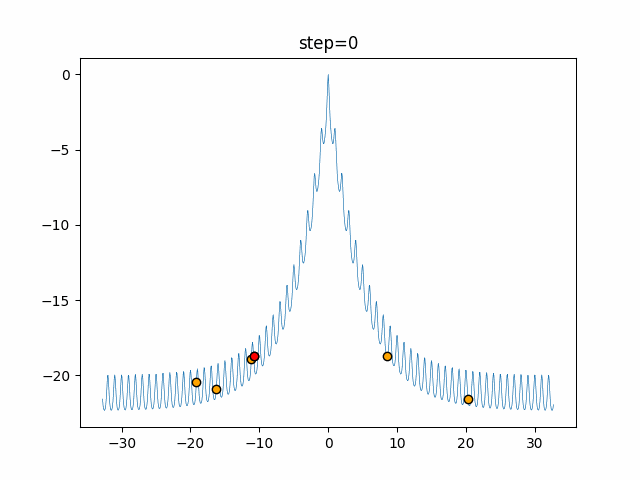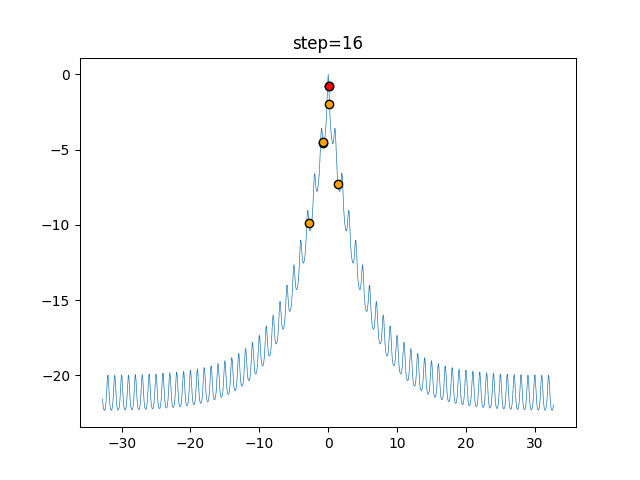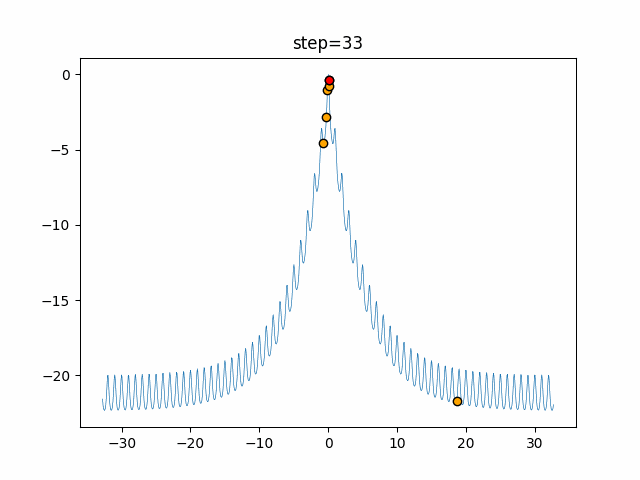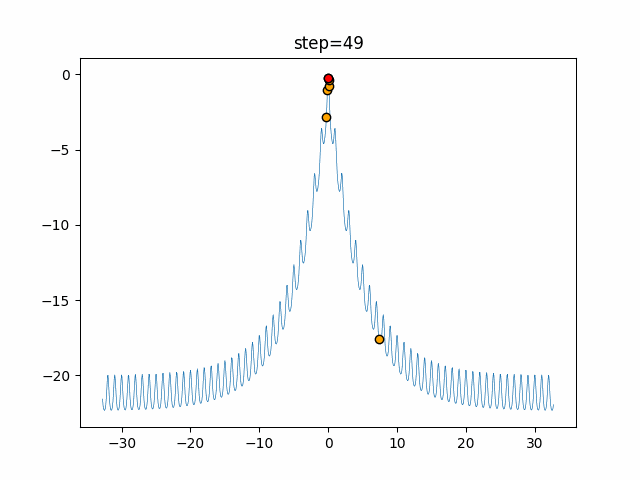
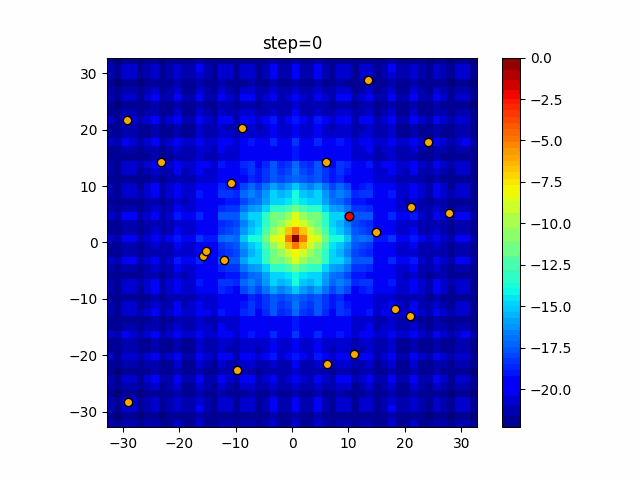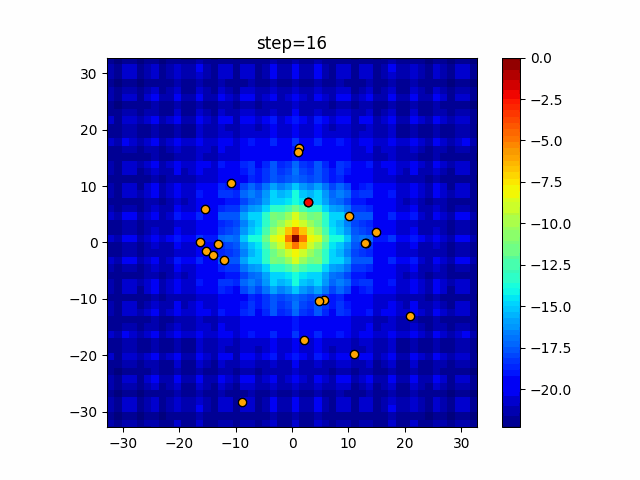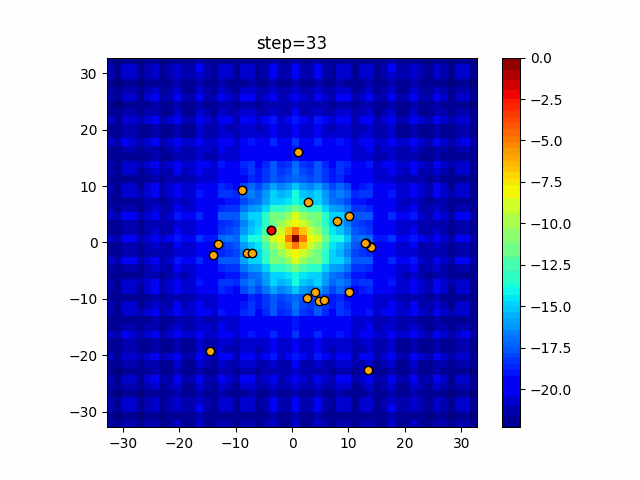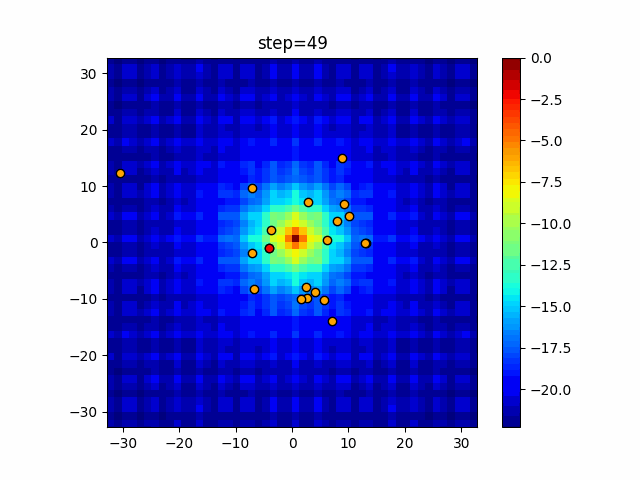
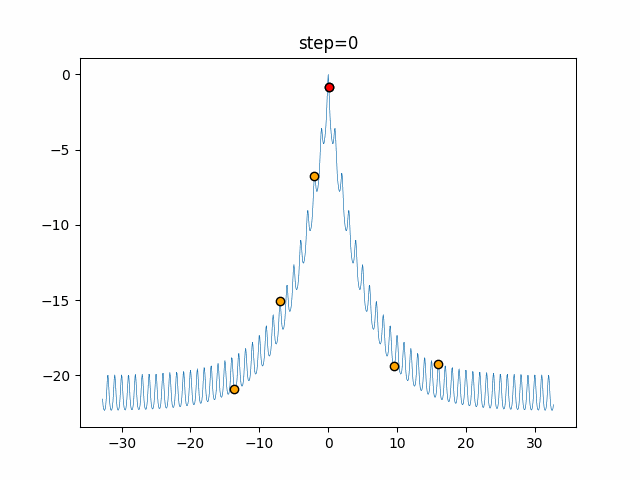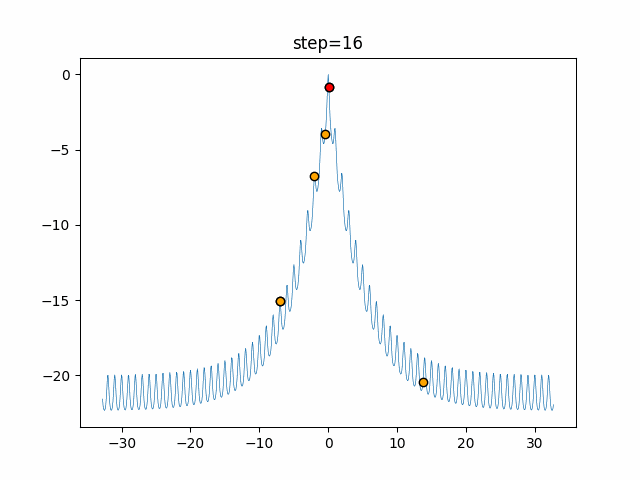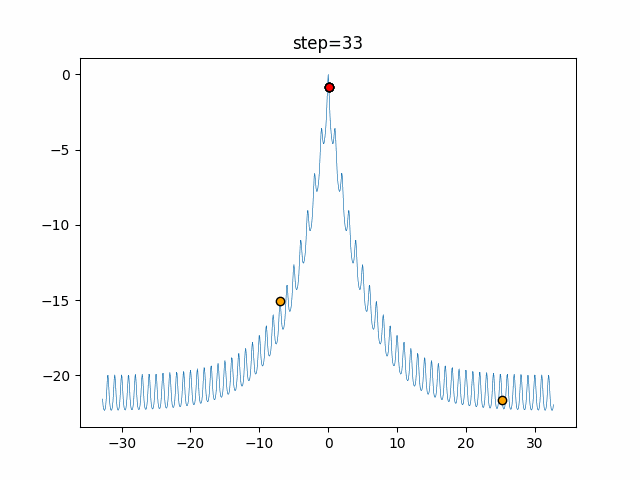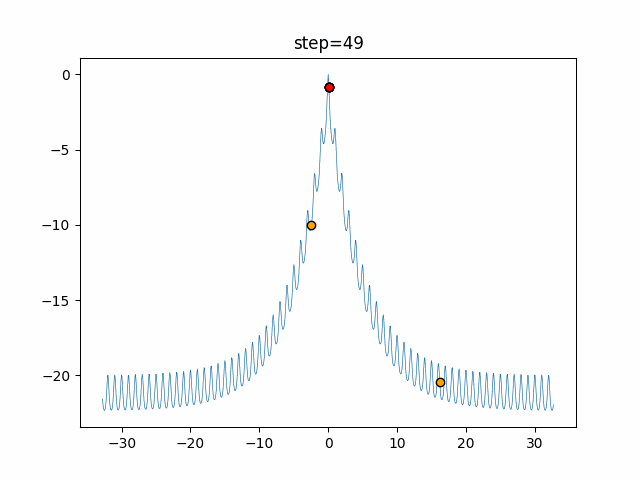
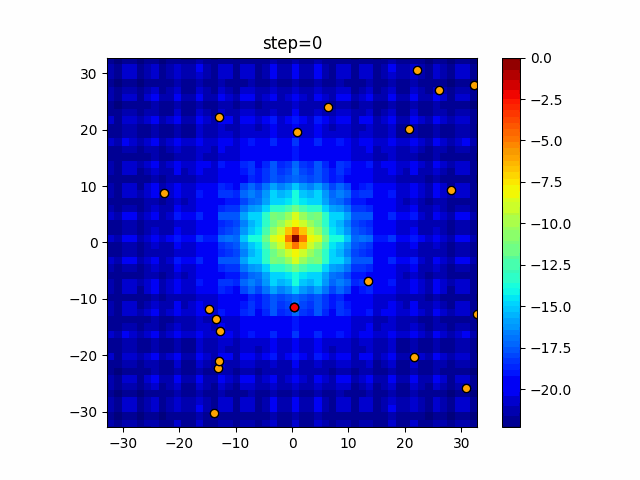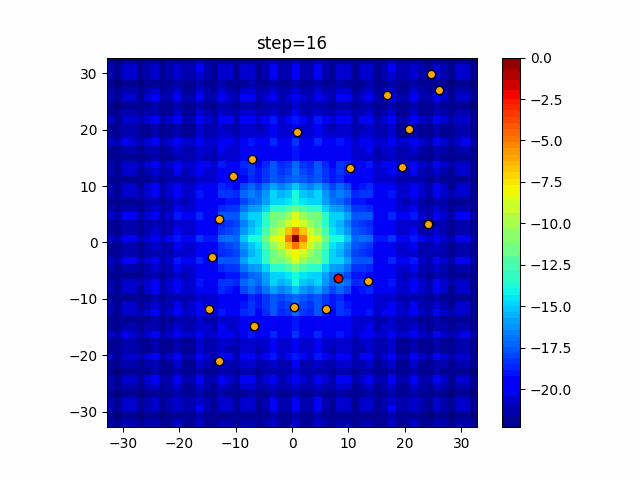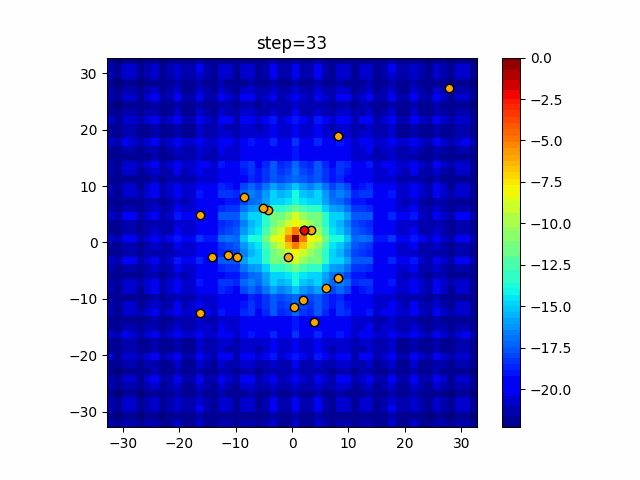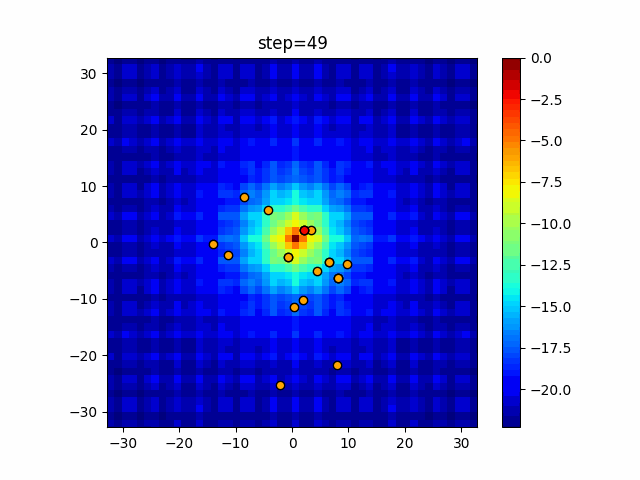
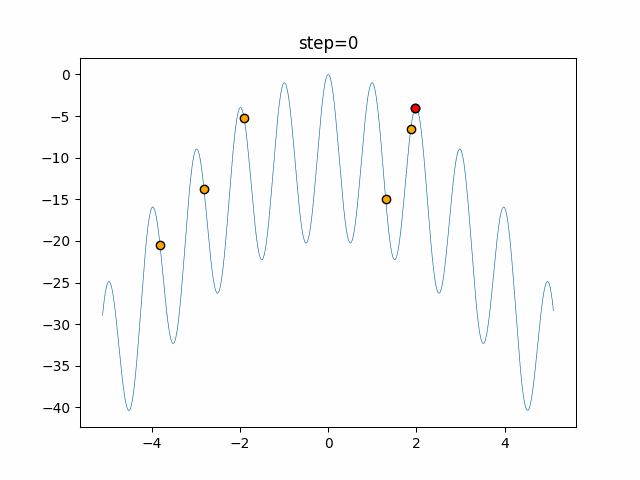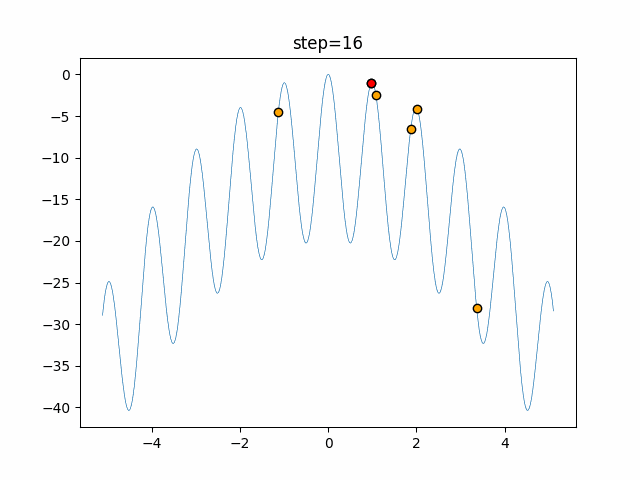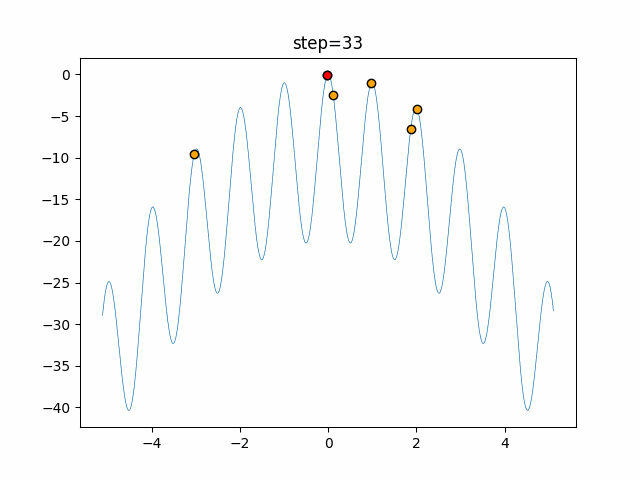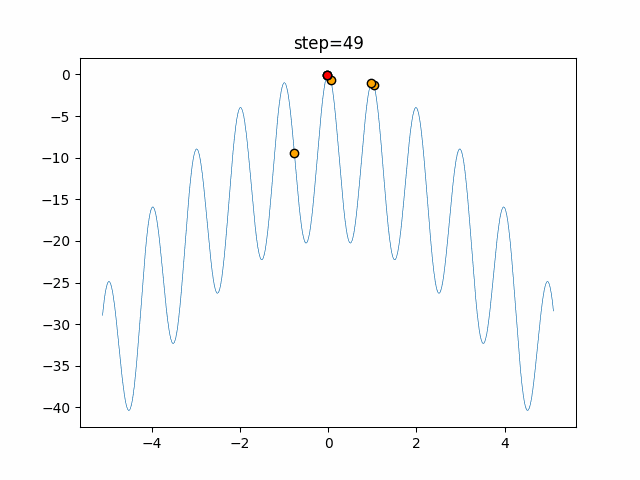
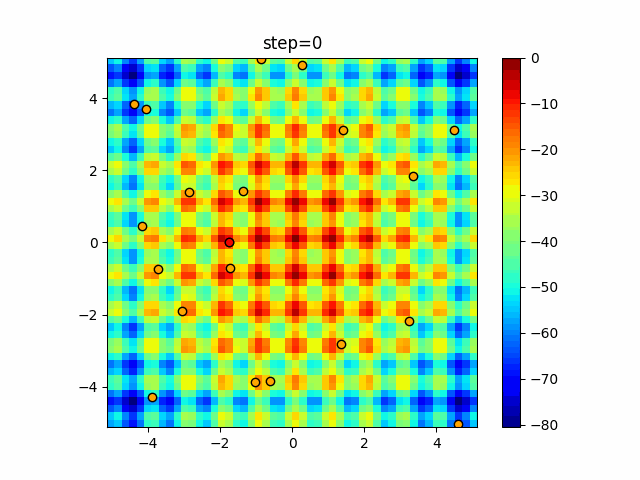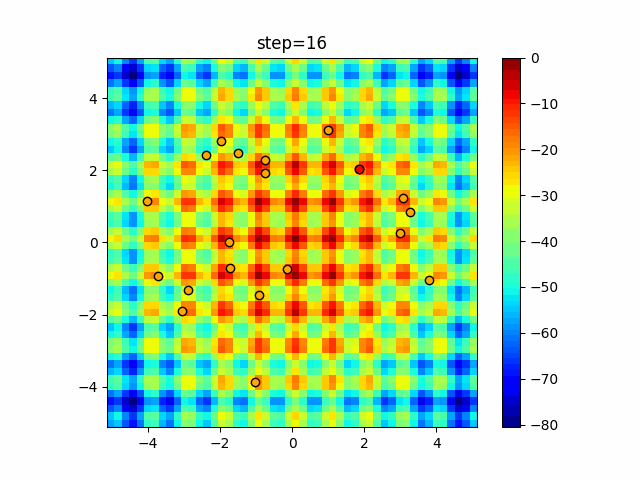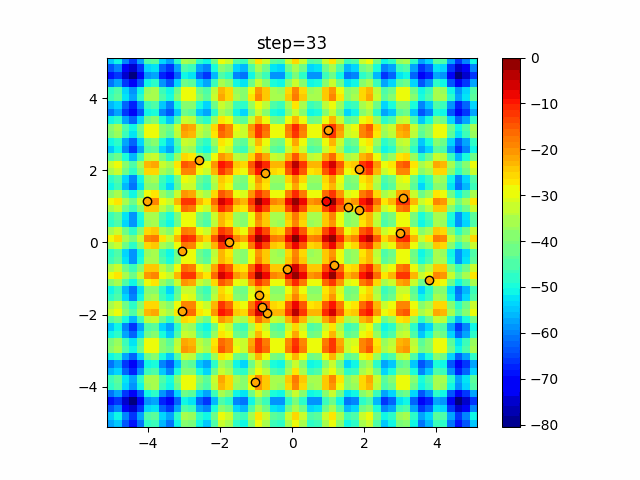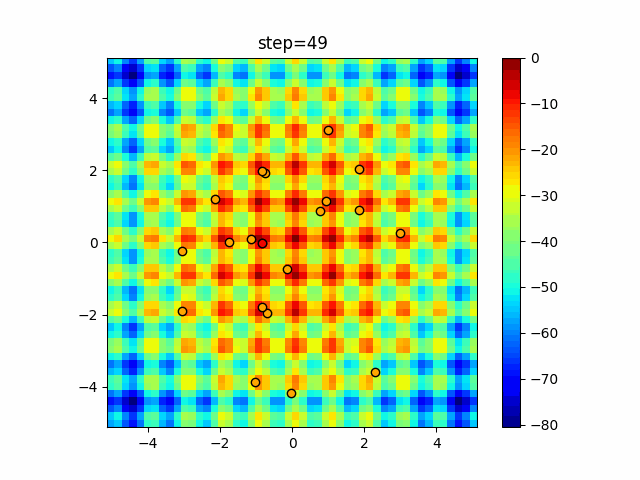
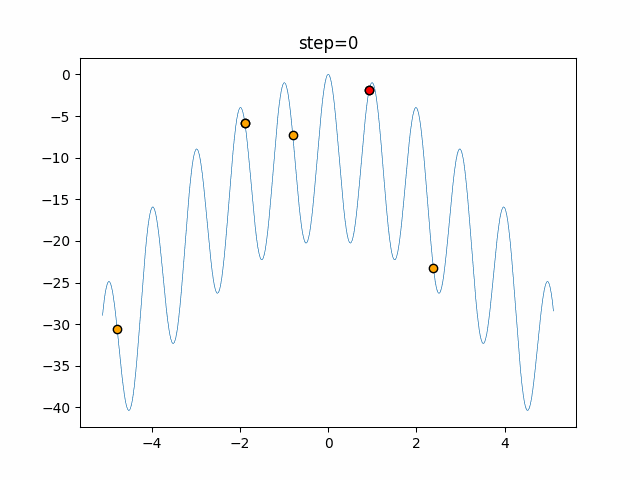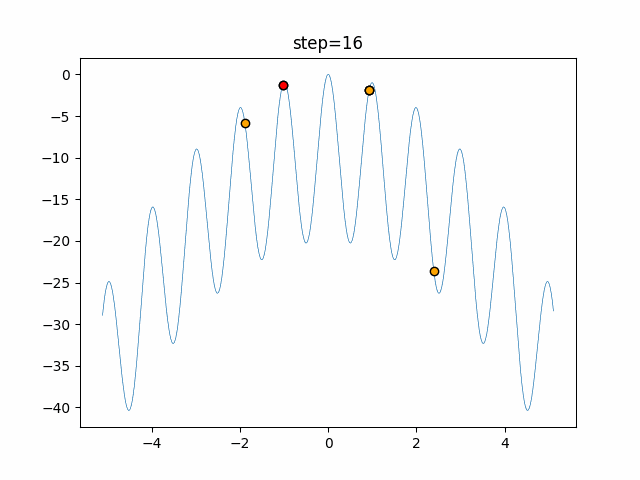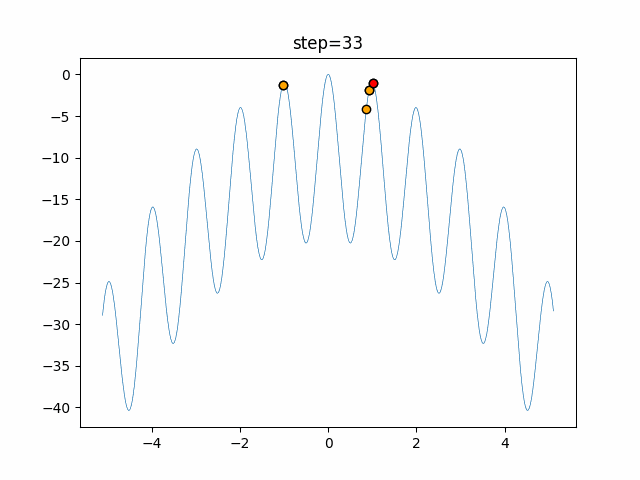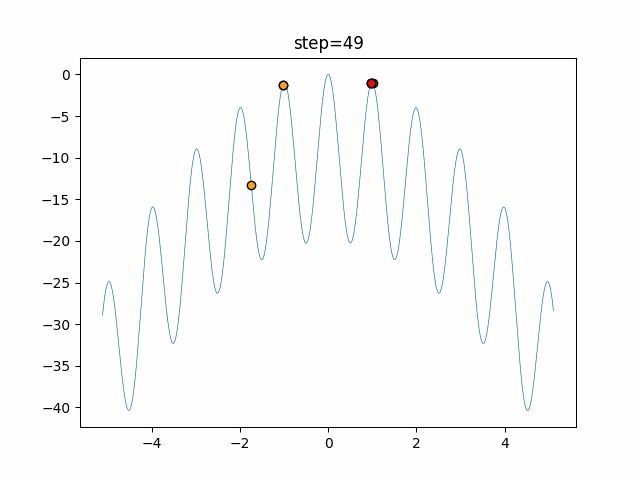
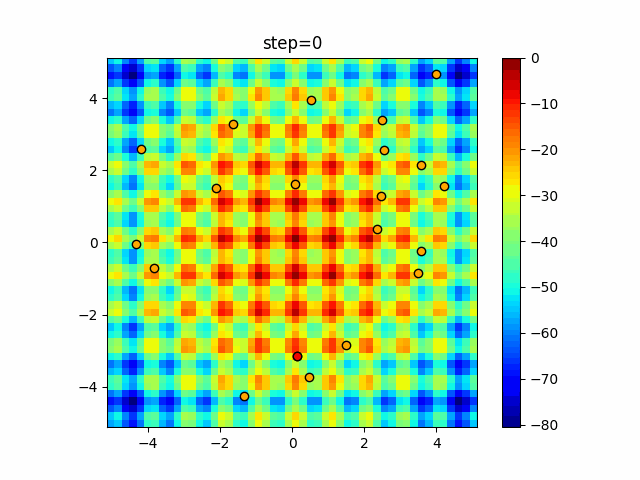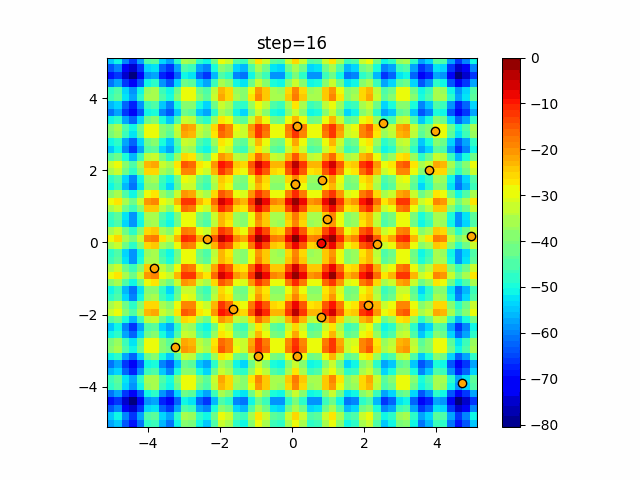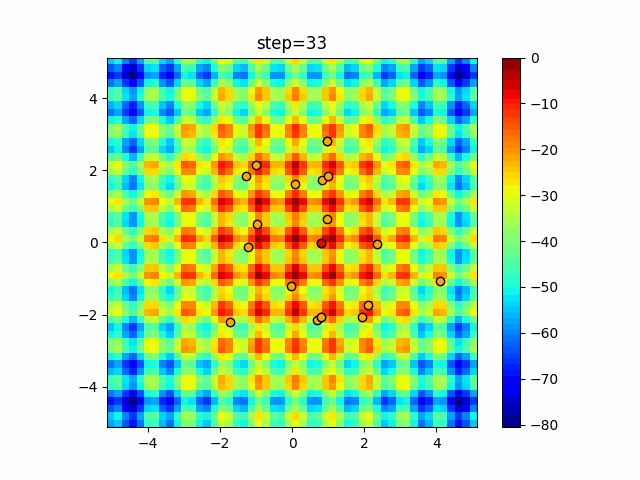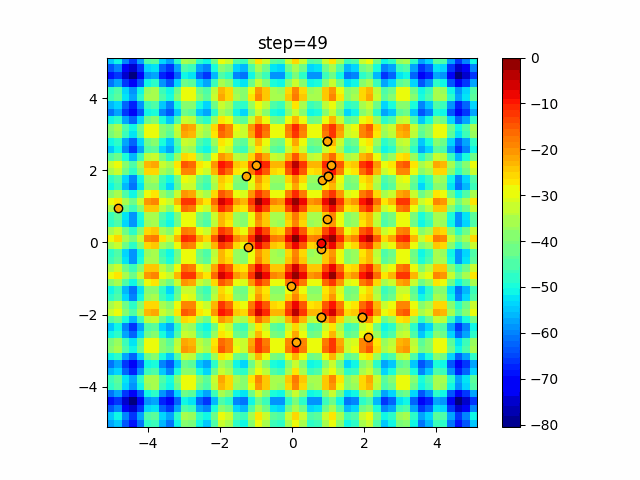
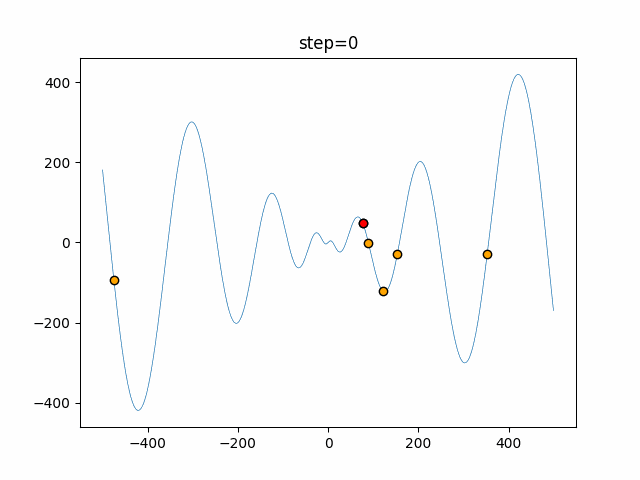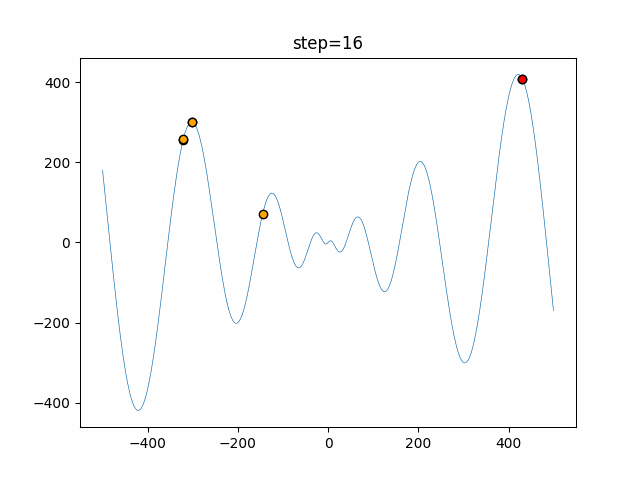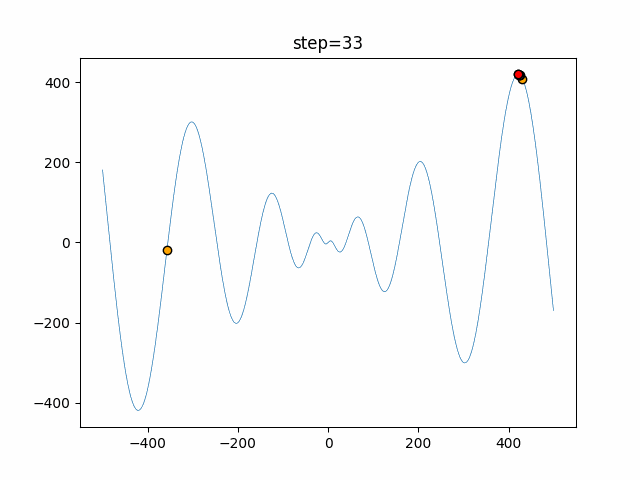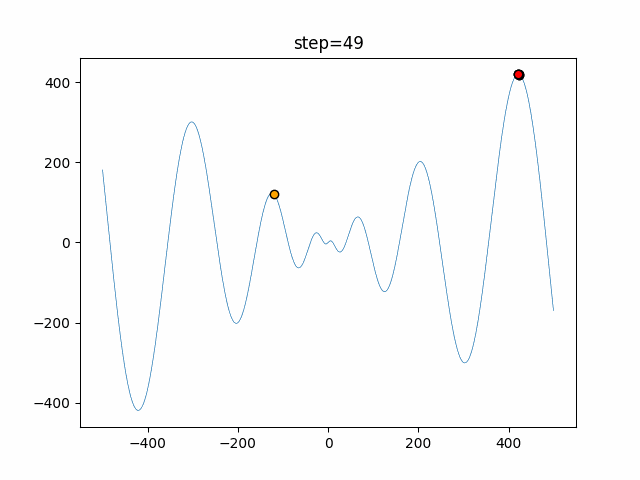
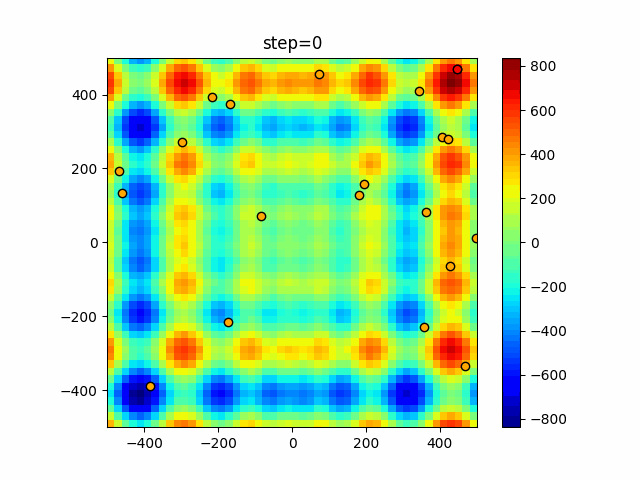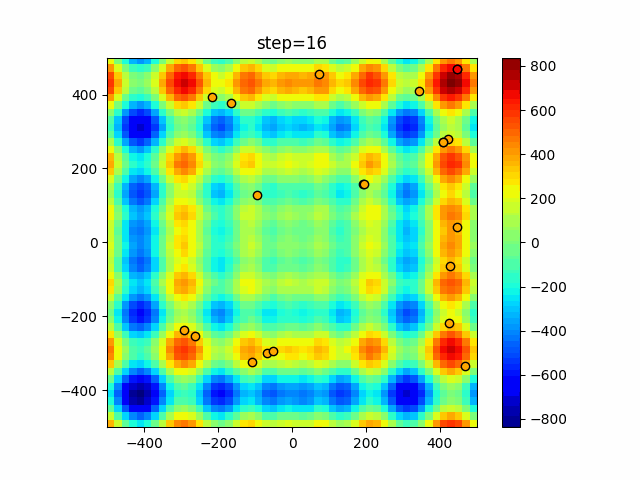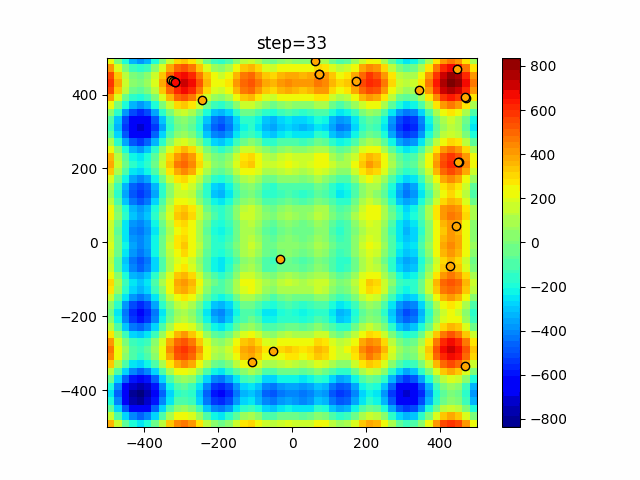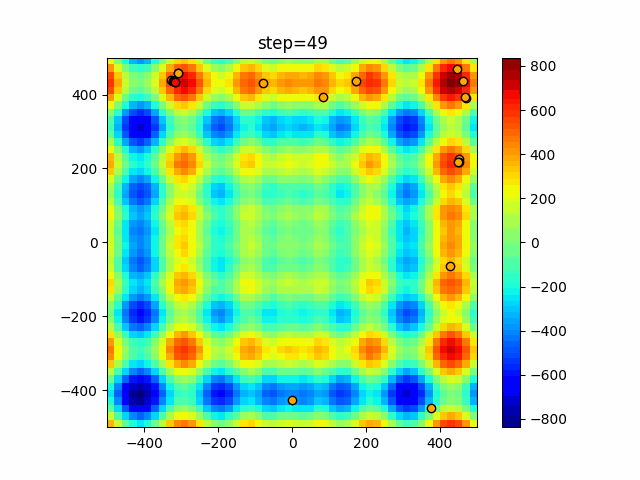
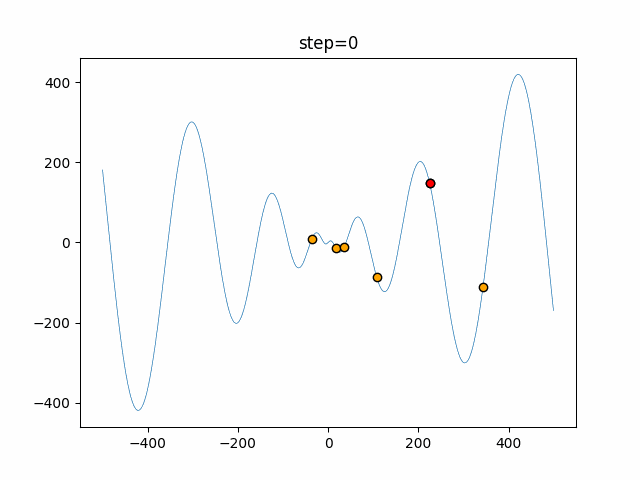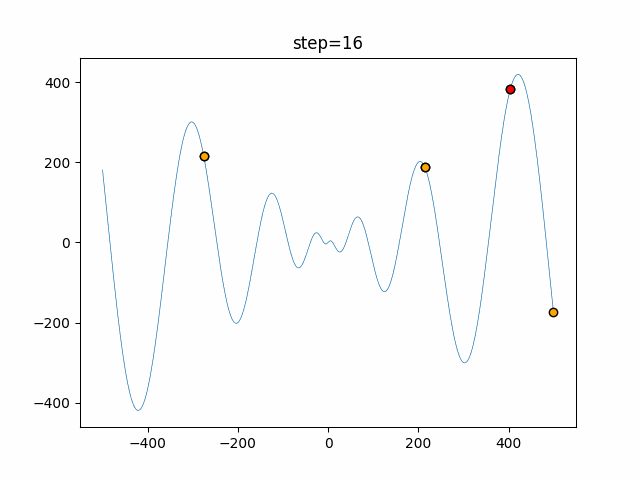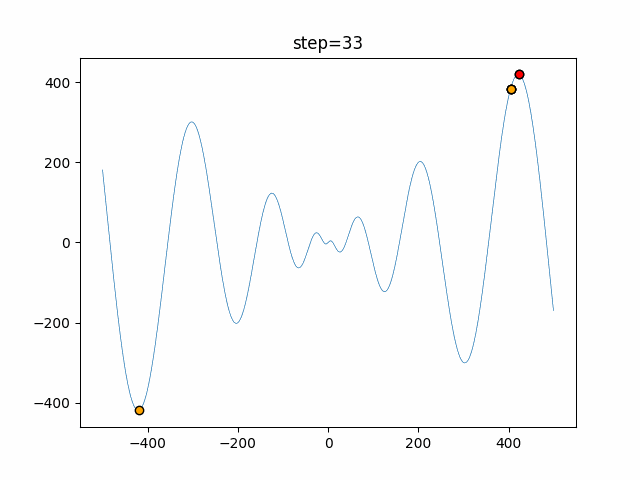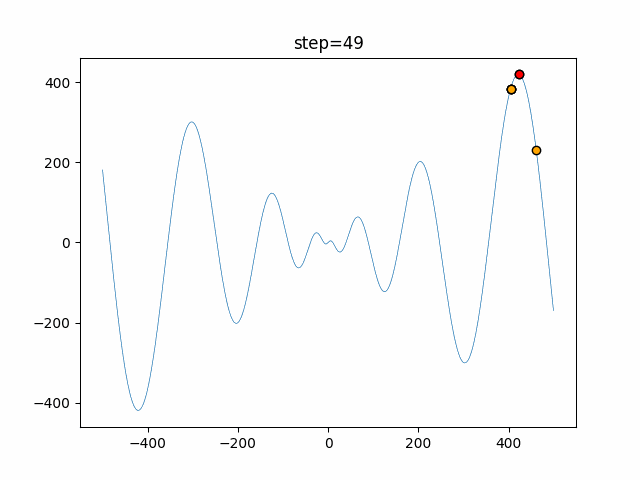
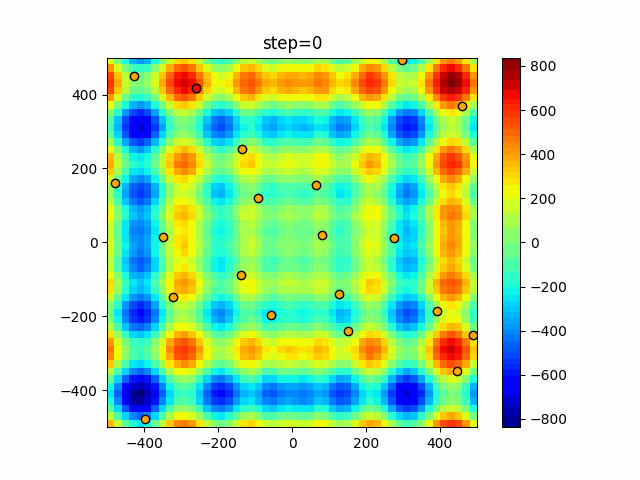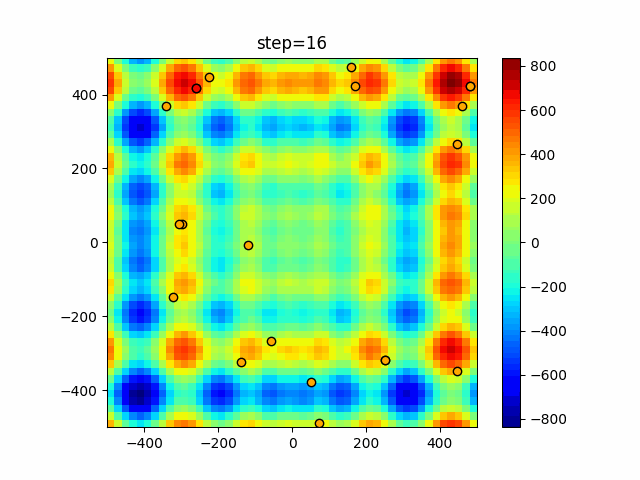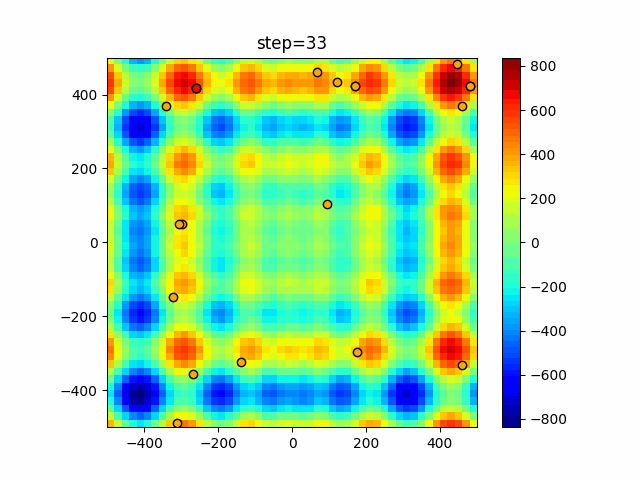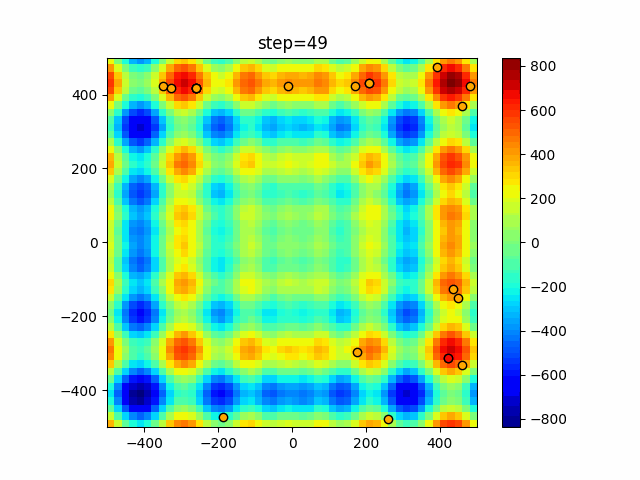
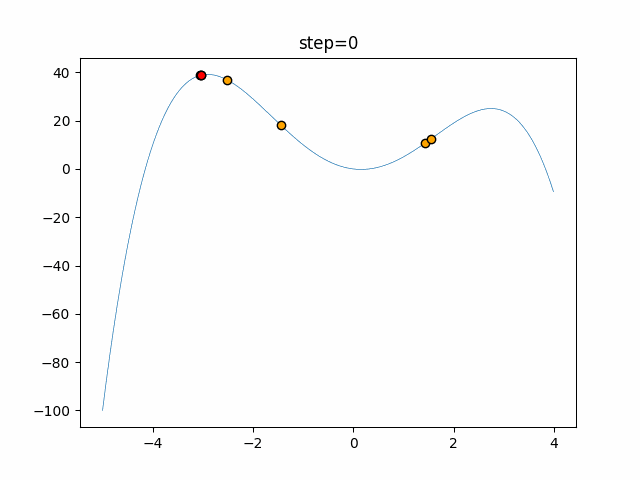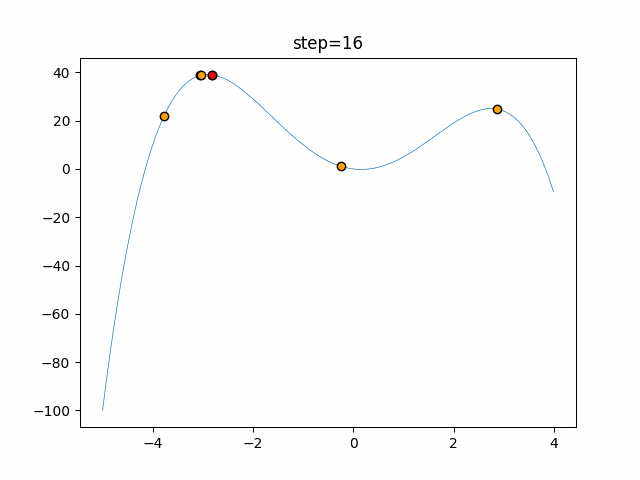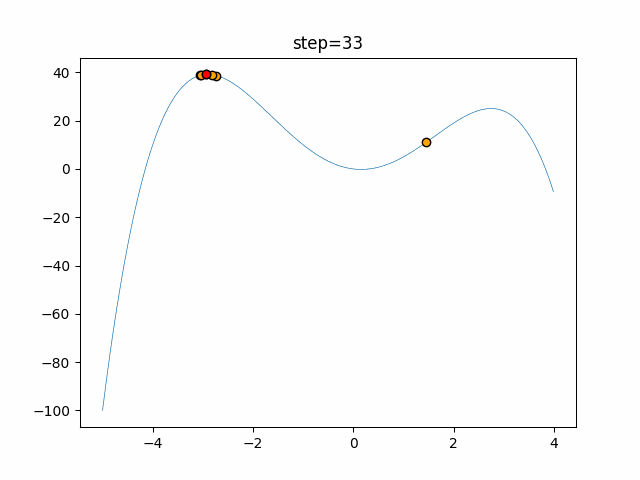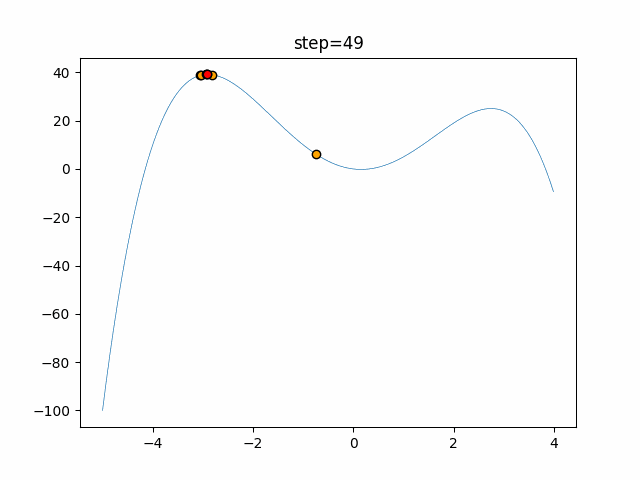
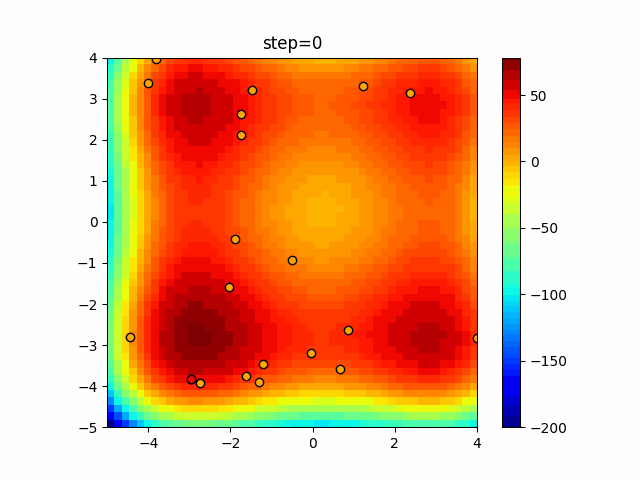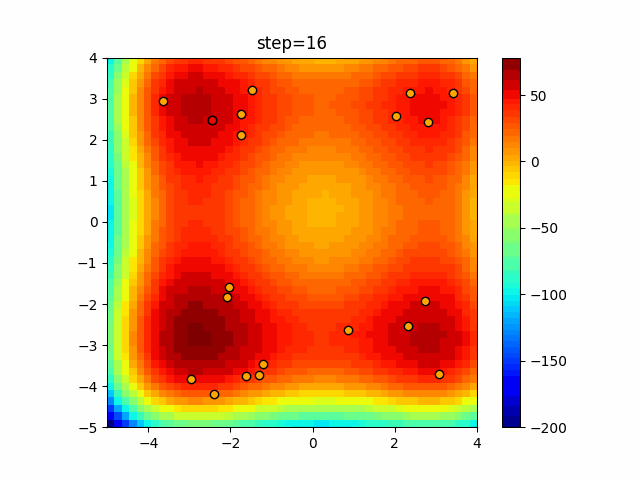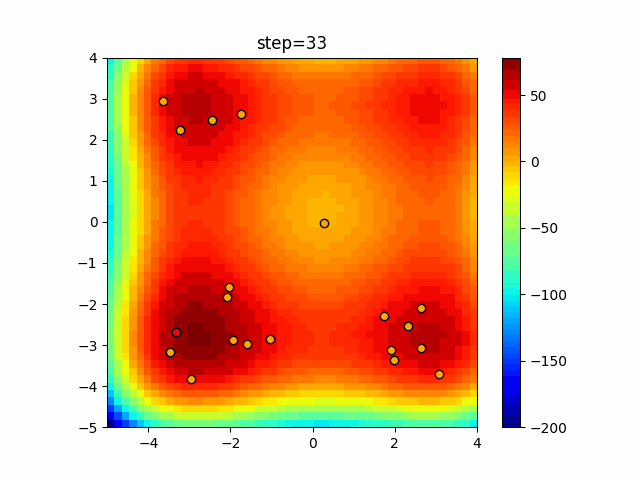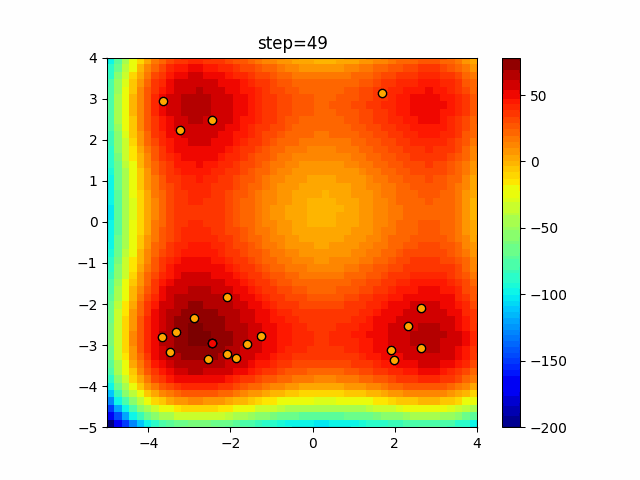
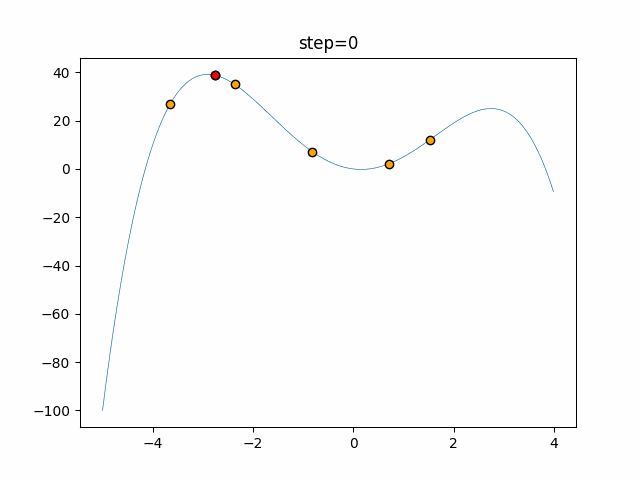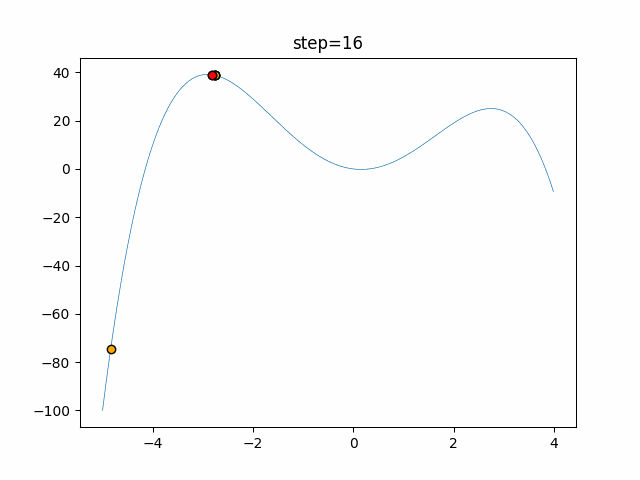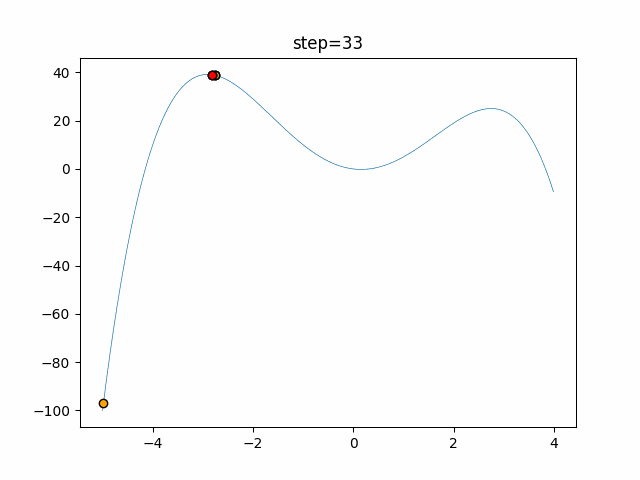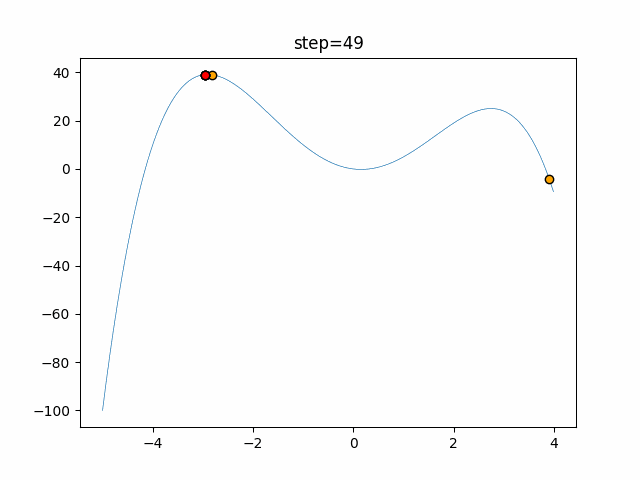
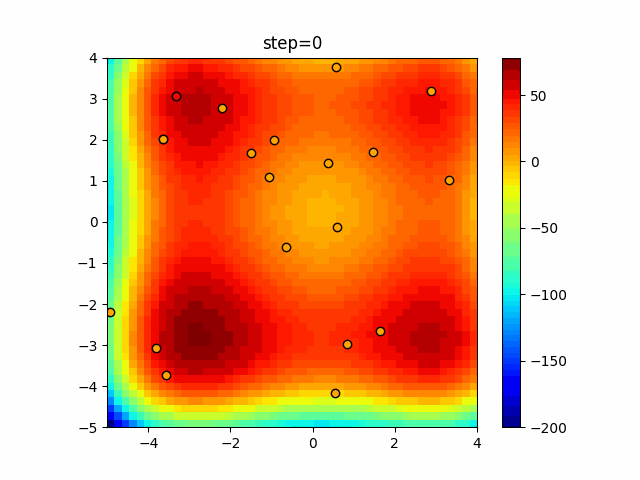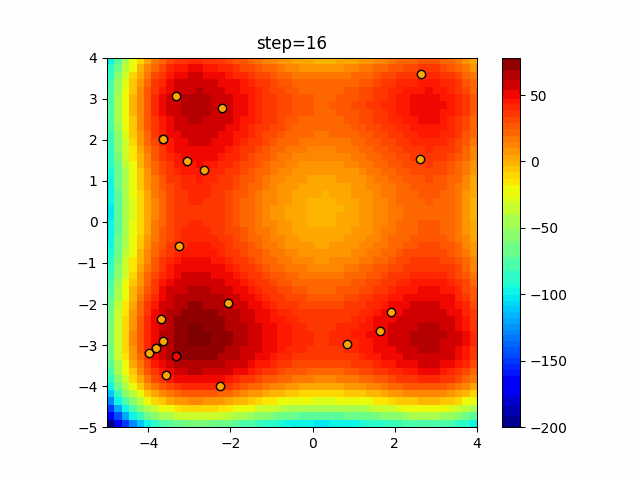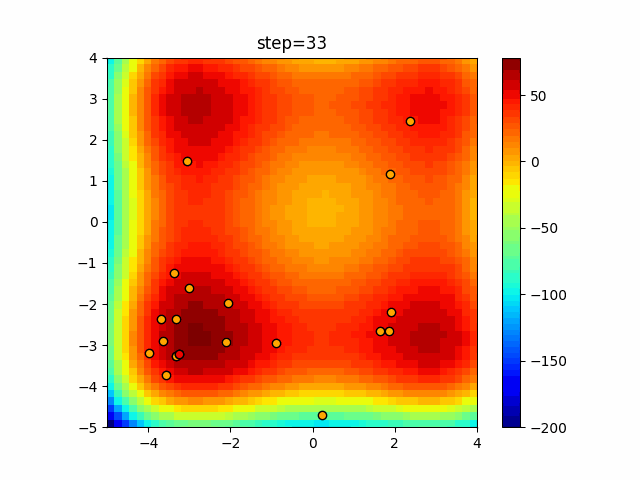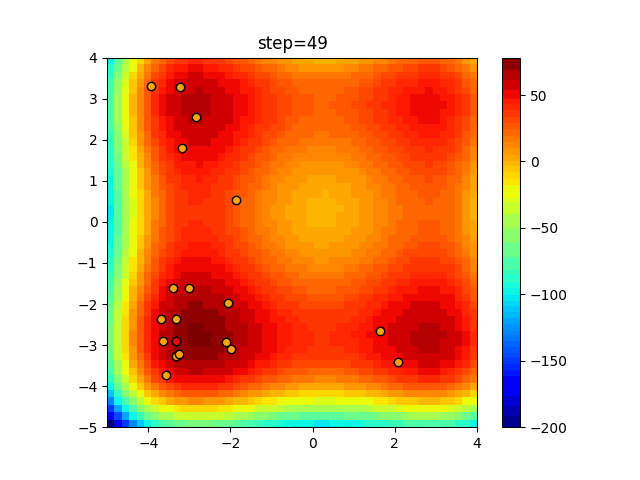
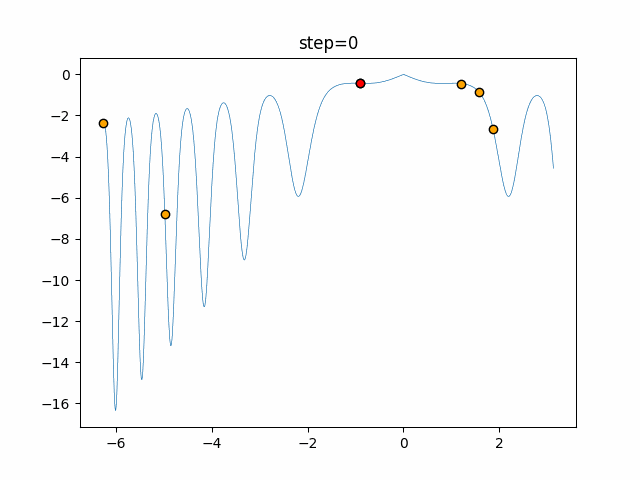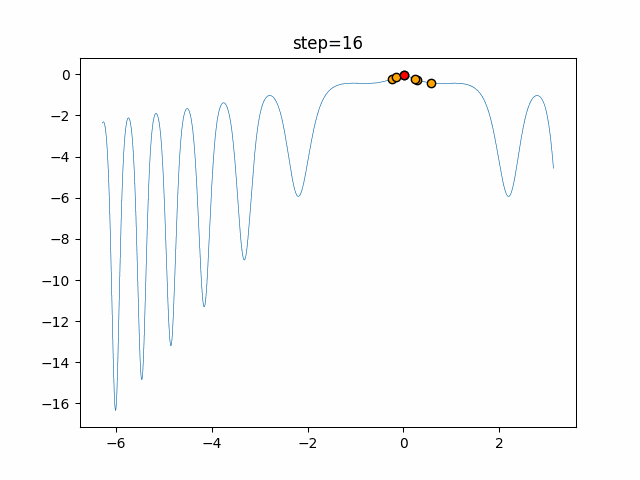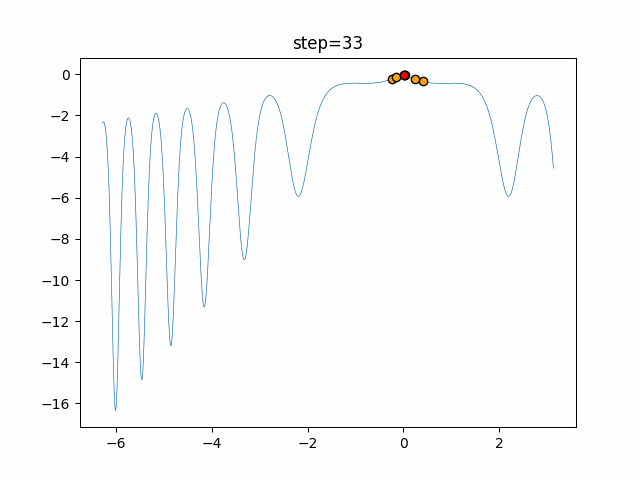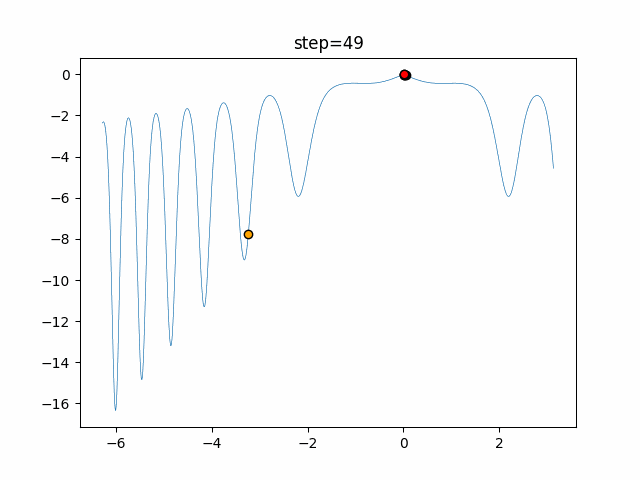
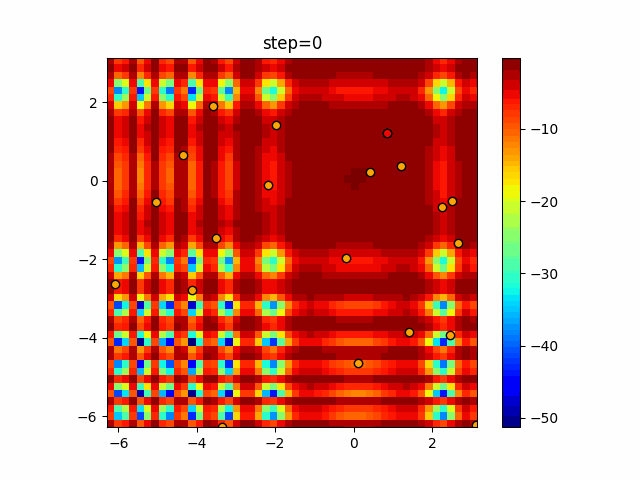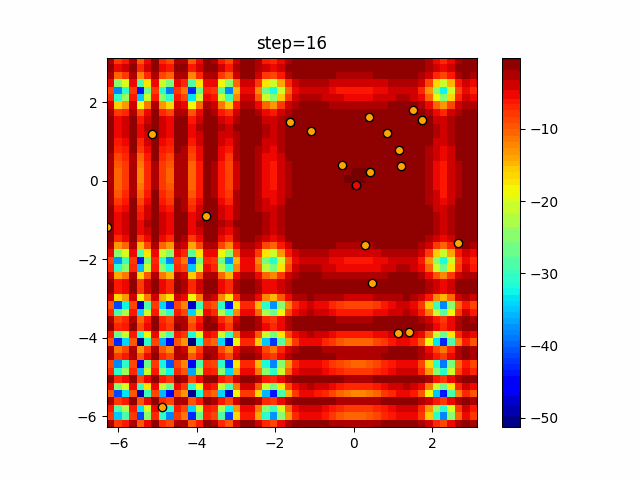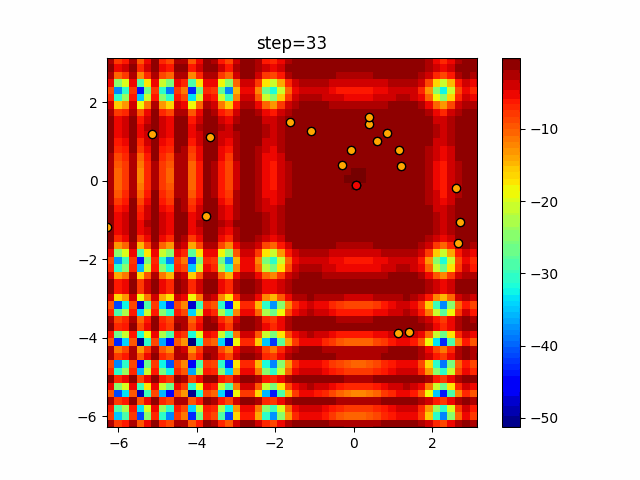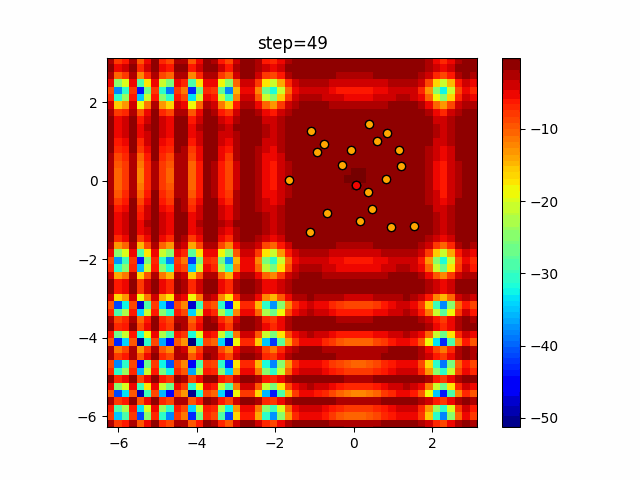
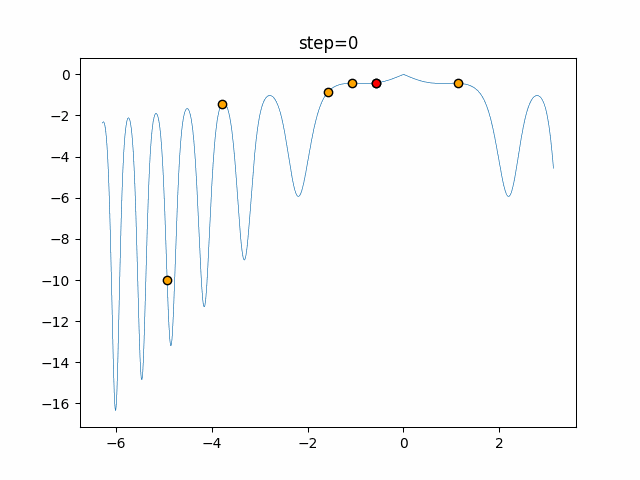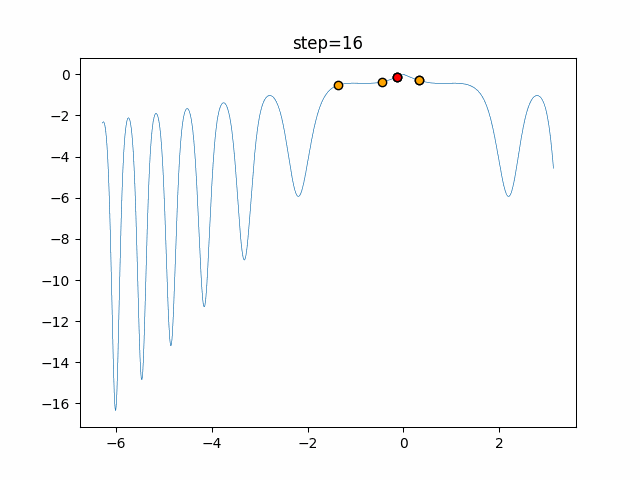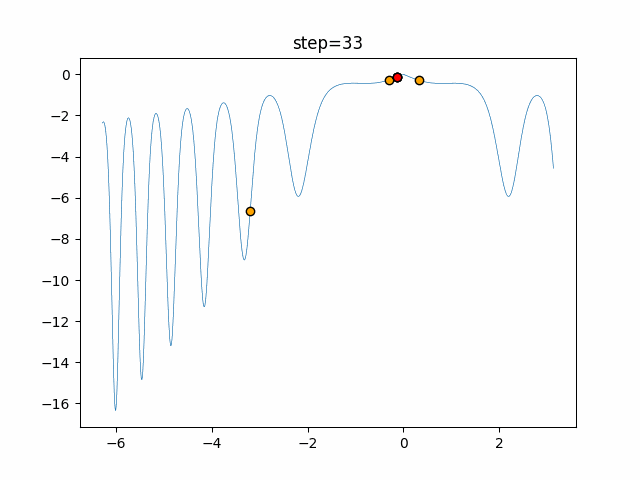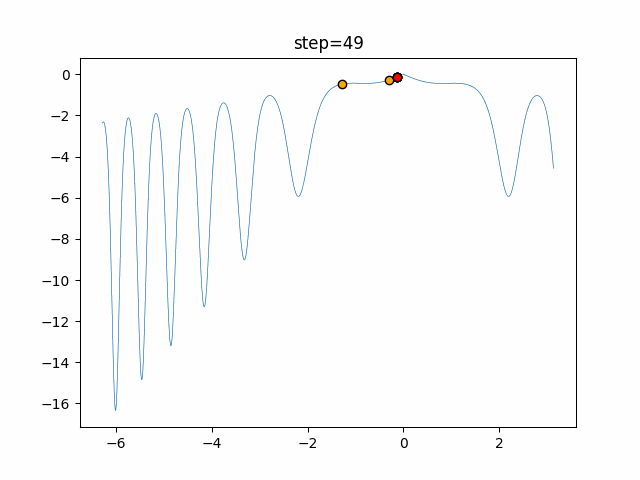
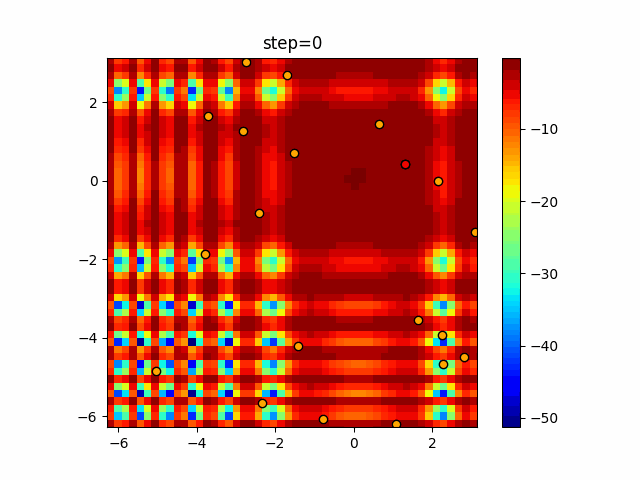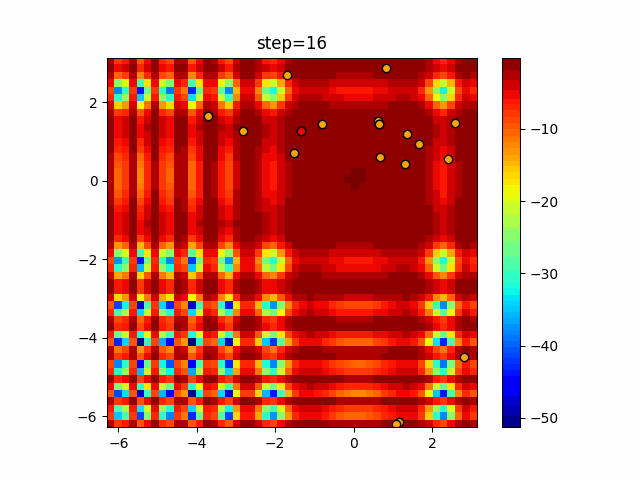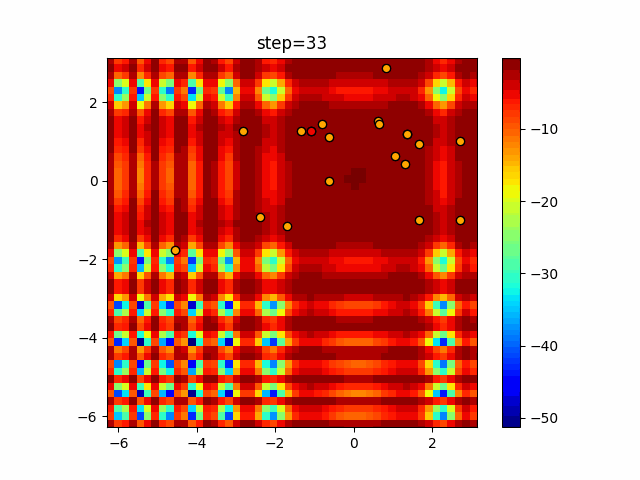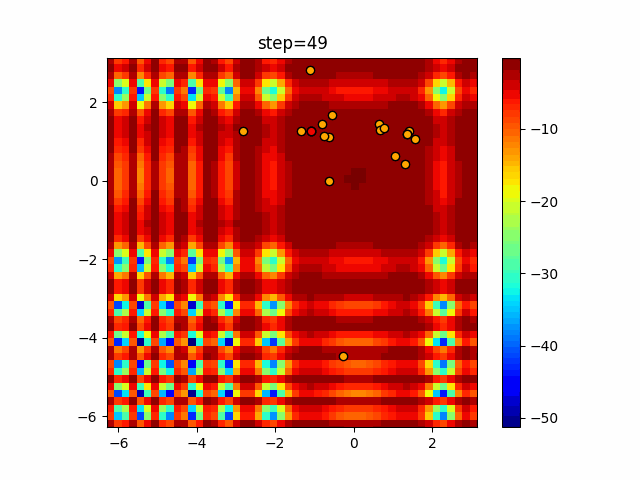
Visualization of actual movement

The 1st dimension is 6 individuals, and the 2nd dimension is 20 individuals, which is the result of 50 steps. The red circle is the individual with the highest score in that step.

The parameters were executed below.

Cuckoo(N, scaling_rate=1.0, levy_rate=1.0, bad_nest_rate=0.1)
Cuckoo_greedy(N, epsilon=0.5, bad_nest_rate=0.1)

function_Ackley

Cuckoo
1D

Cuckoo_greedy
1D

function_Rastrigin

Cuckoo
1D

Cuckoo_greedy
1D

function_Schwefel

Cuckoo
1D

Cuckoo_greedy
1D

function_StyblinskiTang

Cuckoo
1D

Cuckoo_greedy
1D

function_XinSheYang

Cuckoo
1D

Cuckoo_greedy
1D

Afterword

The algorithm itself is fairly simple and the accuracy seems to be quite good. It was the most difficult to generate random numbers according to the Levy distribution ...

[PYTHON] We will implement the optimization algorithm (cuckoo search)

Introduction

Cuckoo search

Overview

algorithm

Creating a nest

Regarding the Levy distribution

Whole code

Cuckoo search (ε-greedy)

Whole code

Hyperparameter example

Visualization of actual movement

Afterword