Implement extension field in Python
Overview
In this article, we will briefly explain the finite field and the extension field, and implement the Galois field $ \ GF (2 ^ 4) \ $ in Python. On top of that, we also implement ElGamal encryption on $ \ GF (2 ^ 4) \ $.
About finite field
The following set with prime $ \ p \ $ elements is a finite field $ \ \ mathbb {F} _p \ $.
\mathbb{F}_p = \{ 0, 1, \cdots, p-1\}.
Addition and multiplication are defined in this set, for example, when $ \ p = 5 \ $,
2 + 3 = 0, \ \ 1 + 3 = 4,\ \ 3 + 4 = 2,\\
2 \times 3 = 1,\ \ 1 \times 3 = 3,\ \ 3 \times 4 = 2.
Note that for $ a, b \ in \ mathbb {F} _p \ $, we calculate as follows.
a + b \pmod{p},\\
a \times b \pmod{p}.
The point is that the original number is a prime number. To explain it in detail, the quotient rings $ \ mathbb {Z} / p \ mathbb {Z} \ $ and $ \ \ mathbb {Z} / n \ mathbb {, which are very similar to finite fields. Have them appear in Z} \ $. However, $ p \ $ is a prime number and $ n \ $ is a non-prime composite number. The quotient ring is a difficult name, but it looks like this:
\mathbb{Z}/p\mathbb{Z} = \{ 0, 1, \cdots, p-1\},\\
\mathbb{Z}/n\mathbb{Z} = \{ 0, 1, \cdots, n-1\}.
Addition and multiplication are also defined in these. So, let's write a "multiplication table" for $ p = 5, n = 6 \ $.
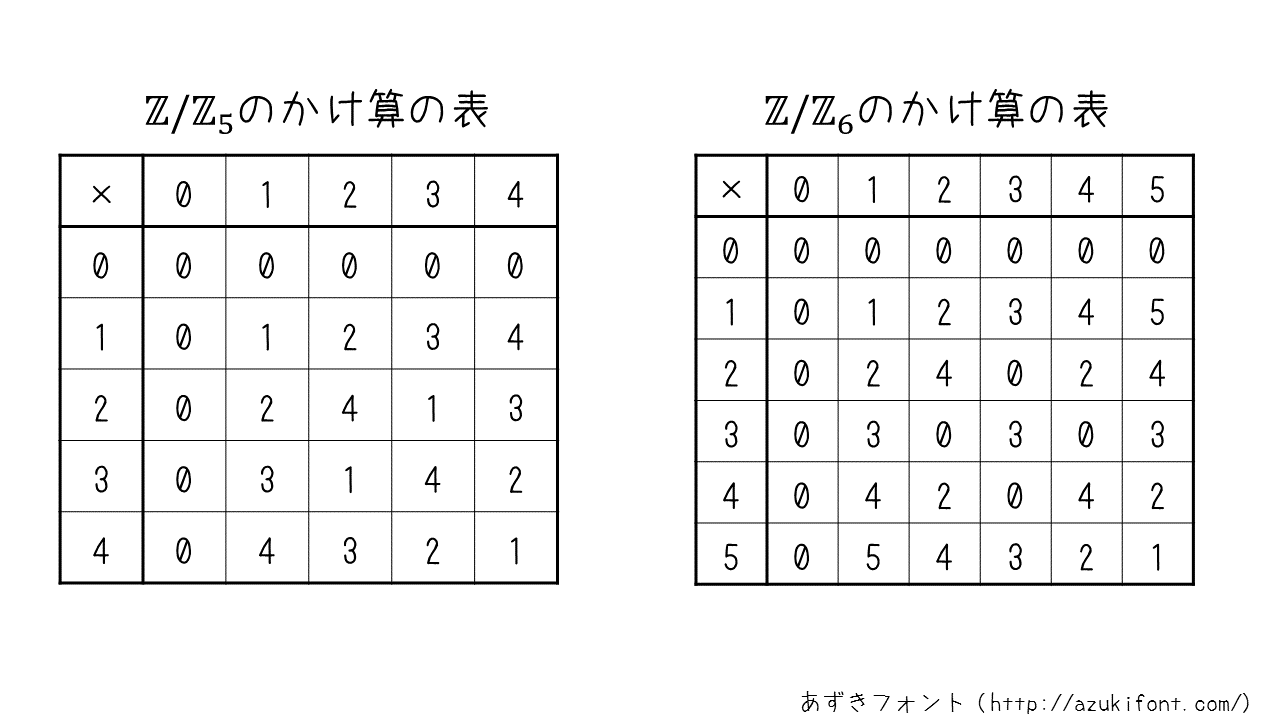
From this table, you may have somehow understood the difference between the two quotient rings. That is, in a quotient ring whose original number is a prime number, the result of multiplication will not be $ \ 0 \ $ unless $ 0 \ $ is used. Therefore, there is no need to worry that complicated calculations such as multiplication many times may make meaningful calculations such as encryption and decryption meaningless due to the appearance of $ \ 0 \ $. .. In algebra, the "quotient ring whose original number is a prime number" is called a "finite field", which is useful in cryptography. For example, in the case of $ \ mathbb {F} _ {23} \ $
\textbf{a} = \{ 2^j : j\in \{0,1,\cdots, 11\}\}.
About the extension field
In the previous discussion, if the original number is a composite number, a finite field could not be created. In fact, if $ n = 2 ^ 4 $,
2\times 8 = 0, 4\times4=0.
However, even in the case of composite numbers, a finite field can be created by using an irreducible polynomial. Irreducible polynomials are polynomials that cannot be decomposed any further. For example
x^4 + x +1 is an irreducible polynomial,\\
x^4 + 1 \Is not
Because each coefficient is $ \ \ {0, 1 \} \ $,
x^4 + 1 = x^4 + 2x^2 + 1 = (x^2 + 1)^2.
Now, let's create a finite field. Equations made with irreducible polynomials: When the solution of $ x ^ 4 + x + 1 = 0 \ $ is $ \ \ alpha \ $
\textbf{a} = \{ \alpha^j : j\in \{0,1,\cdots, 2^4-2\}\}
Are all different original collections. First of all, the following four elements are different because they cannot be decomposed any more.
\alpha^0, \alpha^1, \alpha^2, \alpha^3.
Others can be confirmed by using $ \ alpha ^ 4 + \ alpha + 1 = 0 \ $.
\alpha^4 = \alpha + 1,\ \alpha^5 = \alpha^2 + \alpha, \ \alpha^6 = \alpha^3 + \alpha^2,\ \alpha^7 = \alpha^3 + \alpha + 1,\\
\alpha^8 = \alpha^2 + 1,\ \alpha^9 = \alpha^3 + \alpha,\ \alpha^{10} = \alpha^2 + \alpha + 1,\ \alpha^{11} = \alpha^3 + \alpha^2 + \alpha,\\
\alpha^{12} = \alpha^3 + \alpha^2 + \alpha + 1,\ \alpha^{13} = \alpha^3 + \alpha^2 + 1,\ \alpha^{14} = \alpha^3 + 1,\ \alpha^{15}=1.
As mentioned above, all elements can be represented by $ \ \ alpha ^ 0, \ alpha ^ 1, \ alpha ^ 2, \ alpha ^ 3 \ $. If the coefficients of $ \ alpha ^ 3, \ alpha ^ 2, \ alpha ^ 1, \ alpha ^ 0 \ $ are regarded as bits,
\alpha^0 \leftrightarrow 1,\ \alpha^1\leftrightarrow 2,\ \alpha^2\leftrightarrow 4,\ \alpha^3\leftrightarrow 8,\
\alpha^4 \leftrightarrow 3,\ \alpha^5\leftrightarrow 6,\\ \alpha^6\leftrightarrow 12,\ \alpha^7\leftrightarrow 11,\
\alpha^8 \leftrightarrow 5,\ \alpha^9\leftrightarrow 10,\ \alpha^{10}\leftrightarrow 7,\\
\alpha^{11}\leftrightarrow 14,\ \alpha^{12} \leftrightarrow 15, \alpha^{13}\leftrightarrow 13,\ \alpha^{14}\leftrightarrow 9,\ \alpha^{15}\leftrightarrow 1.
If we can establish an operation method that consists of $ \ textbf {a} \ $, we can realize the finite field $ \ \ mathbb {F} _ {2 ^ 4} \ $.
Implement extension field
The Galois field $ \ GF (2 ^ 4) \ $ is used as the extension field.
Source and index of Galois field GF (16)
Create the original set of Galois field $ \ GF (2 ^ 4) \ $ $ \ \ textbf {a} = (a_i) \ $ and the index table $ \ \ textbf {b} = (b_i) \ $.
\textbf{a}= \{ 1, 2, 4, 8, 3, 6 , 12, 11, 5, 10, 7, 14, 15, 13, 9, 1\},\\
\textbf{b}= \{0, 0, 1, 4, 2, 8, 5, 10, 3, 14, 9, 7, 6, 13, 11, 12 \}.
I'm worried about $ b_0 = 0 \ $, but it doesn't matter if it's $ \ 0 \ $ or $ \ 100 \ $, but anyway, it corresponds to $ \ a_0 = 1, \ b_1 = 0 \ $. I hope you can. That is, $ \ b_0 = 0 \ $ for convenience. You don't have to worry about it.
galfield.py
# -*- coding: utf-8 -*-
def galois2(k, l):
p = pow(2, k)
a = [1]
for i in range(p - 1):
a.append(a[i] * 2)
if a[i + 1] >= p:
a[i + 1] = a[i + 1] - p
a[i + 1] = a[i + 1] ^ l
return a
def table2(a, k):
b = []
for i in range(2 ** k):
b.append(0)
for i in range(1, 2 ** k):
for j in range(2 ** k - 1):
if a[j] == i:
b[i] = j
return b
if __name__ == "__main__":
# x^4 = x + 1 -> [0, 0, 1, 1] -> ll = 3
k = 4
ll = 3
a = galois2(k, ll)
b = table2(a, k)
Implementation of operations on Galois field GF (16)
Addition
a_i + a_j := a_i \oplus a_j.
Subtraction
a_i - a_j := a_i \oplus a_j.
Multiplication
a_i\times a_j:=a_{b_{a_i}+b_{a_j}} = a_{i + j\pmod{2^4-1}}.
Divide
a_i / a_j:=a_{b_{a_i}-b_{a_j}} = a_{i - j\pmod{2^4-1}}.
Power multiplication
a_i^n := a_{b_{a_i} \cdot n} = a_{i \cdot n\pmod{2^4-1}}.
The operations that should be specially implemented are multiplication, division, and power multiplication.
galois.py
# -*- coding: utf-8 -*-
from galfield import galois2, table2
def gtimes2(k, a, b, s, t):
return a[(b[s] + b[t]) % (2 ** k - 1)]
def gdiv2(k, a, b, s, t):
return a[(b[s] - b[t]) % (2 ** k - 1)]
def gpow2(k, a, b, s, l):
return a[(b[s] * l) % (2 ** k - 1)]
if __name__ == "__main__":
k = 4
ll = 3
a = galois2(k, ll)
b = table2(a, k)
# Example of caluc over galois field
# ADD & SUB
print a[2] ^ a[5]
# MUL & DIV
print gtimes2(k, a, b, a[2], a[5])
print gdiv2(k, a, b, a[2], a[5])
# POW
print gpow2(k, a, b, a[2], 3)
[Appendix] Implemented ElGamal encryption on extension field
ElGamal encryption (ElGamal encryption) is a public key cryptography proposed by Taher Elgamal of Egypt in 1984. (It's not secure, so I think it's probably not practical ...) There is no special meaning in implementing ElGamal encryption in this article, but since I implemented Galois field, I would like to apply it to something. I wrote it down here as an appendix because I thought about it.
The algorithm of ElGamal encryption is as follows. (Generally, a public key cryptographic algorithm consists of three parts: key generation, encryption, and decryption.) First, the original set of Galois $ \ GF (2 ^ 4) $ $ \ \ textbf { Create a} = (a_i) \ $ and index table $ \ \ textbf {b} = (b_i) \ $.
- Key generation algorithm
x\overset{U}{\leftarrow}\\{ 0, 1, \cdots, 2^4-2\\}. h\leftarrow a_x.
- $ x \ $ is the private key and $ h \ $ is the public key.
- Cryptographic algorithm
- Select plaintext $ \ m \ in \ textbf {a} \ $.
- Generate random numbers $ \ r \ overset {U} {\ leftarrow} \ {0, 1, \ cdots, 2 ^ 4-2 \} \ $.
- $ c_0 \ leftarrow a_r, \ c_1 \ leftarrow m \ cdot h ^ r \ $ is the ciphertext.
- Decoding algorithm
- Decrypted by $ c_1 / c_0 ^ x \ rightarrow m \ $.
gElGamal.py
# -*- coding: utf-8 -*-
from random import randint
from galfield import galois2, table2
from galois import gtimes2, gdiv2, gpow2
def GEGKeyGen(a, k):
sk = randint(0, 2 ** k - 2)
pk = a[sk]
return [sk, pk]
def GEGEnc(m, a, pk, k):
r = randint(0, 2 ** k - 2)
return [a[r], gtimes2(k, a, b, m, gpow2(k, a, b, pk, r))]
def GEGDec(c, a, k, sk):
return gdiv2(k, a, b, c[1], gpow2(k, a, b, c[0], sk))
if __name__ == "__main__":
k = 4
ll = 3
a = galois2(k, ll)
b = table2(a, k)
m = a[2]
key = GEGKeyGen(a, k)
sk = key[0]
pk = key[1]
cipher = GEGEnc(m, a, pk, k)
print m == GEGDec(cipher, a, k, sk)
To implement other extensions ...
I hope to find an irreducible polynomial. For example, AES of symmetric key cryptography uses $ \ GF (2 ^ 8) \ $, but its irreducible polynomial is $ \ x ^ 8 + x ^ 4 + x ^ 3 + x ^ 2 + 1 \ $. is. Also, since the bit used in the exclusive OR of galois2 () is $ [0, 0, 0, 1, 1, 1, 0, 1] $, k = 8, ll = 29 in galfield.py. You can express $ \ GF (2 ^ 8) \ $ by setting . If you can understand so far, I think that you can implement other extensions by yourself.
Recommended Posts