3. Natural language processing with Python 3-1. Important word extraction tool TF-IDF analysis [original definition]

• When performing natural language processing, one of the specific aims is to "extract important words that characterize a certain sentence."
• When extracting words, first pick up the words that appear most often in the text. Only words that are commonly used in all sentences are at the top of the list in order of frequency of appearance.
• Even if you limit it to nouns using part-of-speech information, many general-purpose words that do not have a specific meaning, such as "thing" and "time", appear at the top, so exclude them as stop words. Processing such as is required.

⑴ The idea of TF-IDF

• ** TF-IDF (Term Frequency --Inverse Document Frequency) **, literally translated as "Term Frequency --Inverse Document Frequency".
• ** The idea of judging a word that appears frequently but the number of documents in which the word appears is small **, that is, a word that does not appear everywhere, as a ** characteristic and important word ** is.
• Most of them are for words, but they can also be applied to letters and phrases, and various document units can be applied.

⑵ Definition of TF-IDF value

** Occurrence frequency $ tf $ multiplied by coefficient $ idf $, which is an indicator of rarity **

• tfidf=tf×idf
• $ tf_ {ij} $ (frequency of occurrence of word $ i $ in document $ j $) × $ idf_ {i} $ ($ log $, the reciprocal of the number of documents containing word $ i $)

** The frequency of occurrence $ tf $ and the coefficient $ idf $ are defined as follows **

• $ tf_ {ij} = \ dfrac {n_ {ij}} {\ sum_ {k} n_ {kj}} = \ dfrac {number of occurrences of word i in document j} {number of occurrences of all words in document j Sum} $
• idf_{i}=\log \dfrac{|D|}{|\{d:d∋t_{i}\}|} = \log{\dfrac{Number of all documents}{Number of documents containing the word i}}

(3) Mechanism of calculation based on the original definition

#Import Numerical Library
from math import log
import pandas as pd
import numpy as np

➀ Prepare word data list

• Calculate $ tfidf $ of the three target words, assuming that the following word list has been created for the six documents after preprocessing such as morphological analysis.

docs = [
        ["Word 1", "Word 3", "Word 1", "Word 3", "Word 1"],
        ["Word 1", "Word 1"],
        ["Word 1", "Word 1", "Word 1"],
        ["Word 1", "Word 1", "Word 1", "Word 1"],
        ["Word 1", "Word 1", "Word 2", "Word 2", "Word 1"],
        ["Word 1", "Word 3", "Word 1", "Word 1"]
        ]

N = len(docs)

words = list(set(w for doc in docs for w in doc))
words.sort()

print("Number of documents:", N)
print("Target words:", words)

➁ Define a function for calculation

• Define a function that calculates the frequency of occurrence $ tf $, the coefficient $ idf $, and $ tfidf $ multiplied by them in advance.

#Definition of function tf
def tf(t, d):
    return d.count(t)/len(d)
 
#Definition of function idf
def idf(t):
    df = 0
    for doc in docs:
        df += t in doc
    return np.log10(N/df)
 
#Definition of function tfidf
def tfidf(t, d):
    return tf(t,d) * idf(t)

➂ Observe the calculation result of TF

• For reference, let's take a look at the calculation results of $ tf $ and $ idf $ step by step.

#Calculate tf
result = []
for i in range(N):
    temp = []
    d = docs[i]
    for j in range(len(words)):
        t = words[j]     
        temp.append(tf(t,d))
    result.append(temp)
       
pd.DataFrame(result, columns=words)

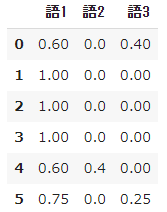
➃ Observe the calculation result of IDF

#Calculate idf
result = []
for j in range(len(words)):
    t = words[j]
    result.append(idf(t))

pd.DataFrame(result, index=words, columns=["IDF"])

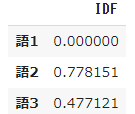
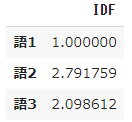
• The coefficient $ idf $ for word 1 that appears in all six documents is 0, and word 2 that appears in only one document has the largest value of 0.778151.

➄ TF-IDF calculation

#Calculate tfidf
result = []
for i in range(N):
    temp = []
    d = docs[i]
    for j in range(len(words)):
        t = words[j]
        temp.append(tfidf(t,d))   
    result.append(temp)

pd.DataFrame(result, columns=words)

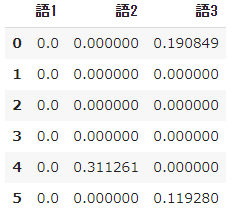
• The coefficient $ idf $ of $ tfidf $ in word 1 is 0, so no matter how many times it appears, it will be 0.
• In addition, TF-IDF is an index originally proposed for the purpose of information retrieval, and for words that do not appear even once, the denominator becomes 0 (so-called division by zero) in calculating $ idf $ and an error occurs. It will be.

⑷ Calculation by scikit-learn

• In response to these problems, scikit-learn's TF-IDF library TfidfVectorizer is implemented with a slightly different definition from the original definition.

# scikit-learn TF-Import IDF library
from sklearn.feature_extraction.text import TfidfVectorizer

• Let's calculate $ tfidf $ using TfidfVectorizer for the word data list of the above 6 documents.

#One-dimensional list
docs = [
        "Word 1 Word 3 Word 1 Word 3 Word 1",
        "Word 1 word 1",
        "Word 1 Word 1 Word 1",
        "Word 1 Word 1 Word 1 Word 1",
        "Word 1 Word 1 Word 2 Word 2 Word 1",
        "Word 1 Word 3 Word 1 Word 1"
        ]

#Generate model
vectorizer = TfidfVectorizer(smooth_idf=False)
X = vectorizer.fit_transform(docs)

#Represented in a data frame
values = X.toarray()
feature_names = vectorizer.get_feature_names()
pd.DataFrame(values,
             columns = feature_names)

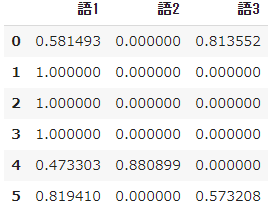
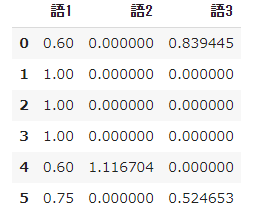
• $ Tfidf $ in word 1 is no longer 0 in each document, and in words 2 and 3, except for documents that were originally 0, the values are different from the original definition.
• So, let's reproduce the result of scikit-learn based on the original definition.

⑸ Reproduce the result of scikit-learn

➀ Change IDF formula

#Definition of function idf
def idf(t):
    df = 0
    for doc in docs:
        df += t in doc
    #return np.log10(N/df)
    return np.log(N/df)+1

• Modify np.log10 (N / df) to np.log (N / df) + 1
• In other words, change the common logarithm with the base 10 to the natural logarithm with the base e as the Napier number e, and add +1.

#Calculate idf
result = []
for j in range(len(words)):
    t = words[j]
    result.append(idf(t))

pd.DataFrame(result, index=words, columns=["IDF"])

➁ Observe the calculation result of TF-IDF

#Calculate tfidf
result = []
for i in range(N):
    temp = []
    d = docs[i]
    for j in range(len(words)):
        t = words[j]
        temp.append(tfidf(t,d))   
    result.append(temp)

pd.DataFrame(result, columns=words)

➂ L2 regularization of TF-IDF calculation results

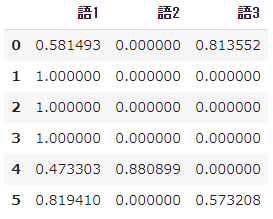
• Finally, ** L2 regularize ** the calculation result of $ tfidf $.
• That is, scale the values and convert them so that they are all squared and summed to 1.
• The reason why regularization is necessary is to count the number of times each word appears in each document, but since each document has a different length, the longer the document, the larger the number of words tends to be.
• By removing the effect of the total number of such words, it is possible to compare the frequency of occurrence of words relatively.

#Calculate the norm value according to the definition only in document 1 as a trial
x = np.array([0.60, 0.000000, 0.839445])
x_norm = sum(x**2)**0.5
x_norm = x/x_norm
print(x_norm)

#Square them and add them up to make sure
np.sum(x_norm**2)

• Let's enjoy here with scikit-learn.

# scikit-Import learn regularization library
from sklearn.preprocessing import normalize

#L2 regularization
result_norm = normalize(result, norm='l2')

#Represented in a data frame
pd.DataFrame(result_norm, columns=words)

• To put it in order, scikit-learn's TF-IDF solves the two drawbacks of the original definition.
• Avoid zero by using the natural logarithm in the formula for the coefficient $ idf $ and adding +1. By the way, the conversion from common logarithm to natural logarithm is about 2.303 times.
• Furthermore, L2 regularization eliminates the effect of the difference in the number of words due to the length of each document.
• The principle of TF-IDF is very simple, but scikit-learn has various parameters, and there seems to be room for tuning depending on the task.