[PYTHON] Erste TensorFlow-Lineare Regression als Einführung
** (Ergänzung: Ich habe einen überarbeiteten Artikel veröffentlicht --http: //qiita.com/TomokIshii/items/0a7041ad337f68f71286) **
Letzte Woche (9. November 2015) wurde Deep Learnins Framework "TensorFlow" veröffentlicht, aber ich war überzeugt, dass die Erklärung des Dokuments "MNIST (Klassifizierung handgeschriebener Zahlen)" Hallo Welt "des maschinellen Lernens ist." Ich kann nicht Wie bei Courseras maschinellem Lernen (Stanford), wenn ich maschinelles Lernen von Anfang an lerne, sehe ich es zunächst persönlich als lineare Regression.
In diesem Artikel untersuchen wir zuerst den Code für die lineare Regression und erstellen dann den Code für die logistische Regression, um ein Gefühl für TensorFlow zu bekommen.
Lineare Regression
In Bezug auf "Theano", den Vorläufer von TensorFlow (zuerst veröffentlicht), wird der Newmu Theano-Tutorials-Code zusätzlich zum Tutorial des Originaldokuments auf GitHub veröffentlicht. (https://github.com/Newmu/Theano-Tutorials)
Es wird ein Funktionscode veröffentlicht, damit Sie "Theano" Schritt für Schritt besser verstehen können. Nach 0_multiply.py (Multiplikation) wird 1_linear_regression.py (Code der linearen Regression) veröffentlicht, aber basierend auf dieser Theano-Version erstellen wir den Code der TensorFlow-Version.
Erstens ist die Theano-Version des Codes.
#Symbolische Variablendefinition"T"Ist theano.Tensor ersetzen
X = T.scalar()
Y = T.scalar()
def model(X, w):
return X * w
#Deklaration gemeinsamer Variablen
w = theano.shared(np.asarray(0., dtype=theano.config.floatX))
y = model(X, w)
#Diagrammdefinition
cost = T.mean(T.sqr(y - Y))
gradient = T.grad(cost=cost, wrt=w)
updates = [[w, w - gradient * 0.01]]
#Funktion
train = theano.function(inputs=[X, Y], outputs=cost, updates=updates, allow_input_downcast=True)
#Lernen durch Schleifenberechnung
for i in range(100):
for x, y in zip(trX, trY):
train(x, y)
Schauen wir uns als nächstes die TensorFlow-Version genauer an.
Bereiten Sie nach dem Import der zugehörigen Module zunächst die zu verwendenden Daten vor. (Die Theano-Version bestand aus Testdaten ohne Abschnitt b, aber hier ist b (= 3.0) enthalten.)
import numpy as np
import tensorflow as tf
trX = np.linspace(-1, 1, 101)
trY = 2 * trX + 3 + np.random.randn(*trX.shape) * 0.33
def lin_model(X, w, b):
return X * w + b
lin_model () ist eine Funktion, die als Regressionsmodell verwendet wird. (Lineare Funktion mit Steigung w und Abschnitt b als Parameter.)
Bereiten Sie als Nächstes die erforderlichen Variablen vor.
w = tf.Variable([0.])
b = tf.Variable([0.])
x = tf.placeholder(tf.float32, shape=(101))
y = tf.placeholder(tf.float32, shape=(101))
w und b sind gewöhnliche Variablen. Der Anfangswert wurde auf [0] gesetzt. Obwohl x und y Begriffe sind, die nur in TensorFlow (Terminologie) vorkommen, werden sie als Platzhalter vorbereitet. Da es sich um einen Platzhalter handelt, gibt es zum Zeitpunkt der Deklaration keinen tatsächlichen Wert, und der tatsächliche Wert wird in der nachfolgenden Programmverarbeitung zugewiesen.
Dann beschreiben wir die wichtige Beziehung zwischen Variablen, die als Graph bezeichnet werden.
y_hypo = lin_model(x, w, b)
cost = tf.reduce_mean(tf.square(y_hypo - y))
Kosten ist eine Kostenfunktion, die der Differenz zwischen Ihrem Modell und den tatsächlichen Daten entspricht. "tf.reduce_mean ()" ist eine Funktion zur Berechnung des Durchschnitts. (Ich denke, "mean ()" ist in Ordnung, aber aus irgendeinem Grund ist es "redu_mean ()" in TensorFlow ... Es scheint, dass es in der Reduktionsfunktionsgruppe ist.)
Definieren Sie dann die Optimizer-Spezifikation und ihre Methode zur Berechnung der Parametersuche.
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
Hier wird der Optimierer der Gradientenabstiegsmethode angegeben und die Lernrate von 0,01 als Argument angegeben.
Über Optimizer
Jetzt bin ich neugierig auf Optimizer, aber TensorFlow unterstützt derzeit Folgendes. http://www.tensorflow.org/api_docs/python/train.html#optimizers
| Optimizer name | Description |
|---|---|
| GradientDescentOptimizer | Optimierer durch Gradientenabstiegsmethode |
| AdagradOptimizer | Optimierer nach AdaGrad-Methode |
| MomentumOptimizer | Momentum-Methodenoptimierer |
| AdamOptimizer | Adam-Methode (Dies ist auch berühmt.) |
| FtrlOptimizer | (Ich habe es zum ersten Mal gehört)"Follow the Regularized Leader"Algorithmus |
| RMSPropOptimizer | (Ich habe es zum ersten Mal gehört) Ein Algorithmus, der die Anpassung der Lernrate automatisiert |
Die Parameter, die eingestellt werden müssen, unterscheiden sich je nach Optimierer. Dieses Mal verwenden wir jedoch den grundlegenden GradientDescentOptimizer. (Die erforderliche Parameterlernrate wurde wie oben beschrieben eingestellt.)
Lineare Regression (Fortsetzung)
Jetzt, da wir fast fertig sind, starten wir eine Sitzung, die den Hauptberechnungsteil zeigt. Die Variablen (Variablen) müssen jedoch vor dem Starten der Sitzung initialisiert werden. Dies ist einzigartig für "Tensor Flow", das nicht in "Theano" enthalten war.
# Initializing
init = tf.initialize_all_variables()
"Variablen vor Beginn einer Sitzung initialisieren" scheint eine Regel zu sein, die oft vergessen wird. Vorerst, wenn Sie überprüfen
- Die Variable von tf.Variable () muss initialisiert werden **.
- Die Variable von tf.placeholder () wird initialisiert ** unnötig **. (Es wird später der Entität zugewiesen.)
- Die Variablen (Konstanten) von tf.constant werden nicht initialisiert **. Es wurde gesagt, dass. In der obigen Liste werden die Variablen mit initialize_all_variable () initialisiert.
Der Sitzungsteil lautet wie folgt.
# Train
with tf.Session() as sess:
sess.run(init)
for i in range(1001):
sess.run(train_step, feed_dict={x: trX, y: trY})
if i % 100 == 0:
print "%5d:(w,b)=(%10.4f, %10.4f)" % (i, sess.run(w), sess.run(b))
Es scheint verschiedene Möglichkeiten zu geben, ein Programm zum Ausführen von Sessoin zu schreiben. Wie oben erwähnt, wird der Sitzungsbegrenzer durch Einfügen in die Anweisung "with" klar und beim Beenden von "with" automatisch geöffnet. Die Sitzung ist geschlossen (), was praktisch ist.
Zum einen ist es schwierig, Zugdaten in TensorFlow anzugeben. Das Geben von Daten (Datenzufuhr) ist der Teil, in dem sich die Verarbeitung ändert, je nachdem, wie mit dem Lernen fortgefahren wird. Wie in der obigen Liste gezeigt, wird jedoch "Feed-Dikt" verwendet. Denken Sie also daran. (Ich studiere diesen Teil noch ...)
Mit dem Obigen werden die Regressionsparameter berechnet. (Es wird gezeigt, wie es für die wahren Werte w = 2,0 und b = 3,0 verwendet wird.)
0:(w,b)=( 0.0135, 0.0599)
100:(w,b)=( 0.9872, 2.6047)
200:(w,b)=( 1.4793, 2.9421)
300:(w,b)=( 1.7280, 2.9869)
400:(w,b)=( 1.8538, 2.9928)
500:(w,b)=( 1.9173, 2.9936)
600:(w,b)=( 1.9494, 2.9937)
700:(w,b)=( 1.9657, 2.9937)
800:(w,b)=( 1.9739, 2.9937)
900:(w,b)=( 1.9780, 2.9937)
1000:(w,b)=( 1.9801, 2.9937)
Das Obige wird zusammengefasst und das Programm erneut veröffentlicht. (Es wurde ein Programm von etwa 30 Zeilen.)
import numpy as np
import tensorflow as tf
trX = np.linspace(-1, 1, 101)
trY = 2 * trX + 3 + np.random.randn(*trX.shape) * 0.33
def lin_model(X, w, b):
return X * w + b
w = tf.Variable([0.])
b = tf.Variable([0.])
x = tf.placeholder(tf.float32, shape=(101))
y = tf.placeholder(tf.float32, shape=(101))
y_hypo = lin_model(x, w, b)
cost = tf.reduce_mean(tf.square(y_hypo - y))
train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cost)
# Initializing
init = tf.initialize_all_variables()
# Train
with tf.Session() as sess:
sess.run(init)
for i in range(1001):
sess.run(train_step, feed_dict={x: trX, y: trY})
if i % 100 == 0:
print "%5d:(w,b)=(%10.4f, %10.4f)" % (i, sess.run(w), sess.run(b))
Informationen zur interaktiven Sitzung
Die obige Liste ist ein Programm, das die Sitzung als (wenn auch kurze) Stapelverarbeitung ausführt. Abgesehen davon unterstützt TensorFlow eine Funktion namens Interaktive Sitzung, mit der Sie sich, wie der Name schon sagt, interaktiv bewegen können. http://tensorflow.org/get_started/basic_usage.html#interactive-usage
Dies bedeutet, dass es gut mit IPython funktioniert, das heißt, es funktioniert gut mit Jupyter Notebook, also habe ich es sofort versucht.
(Es ist so...)
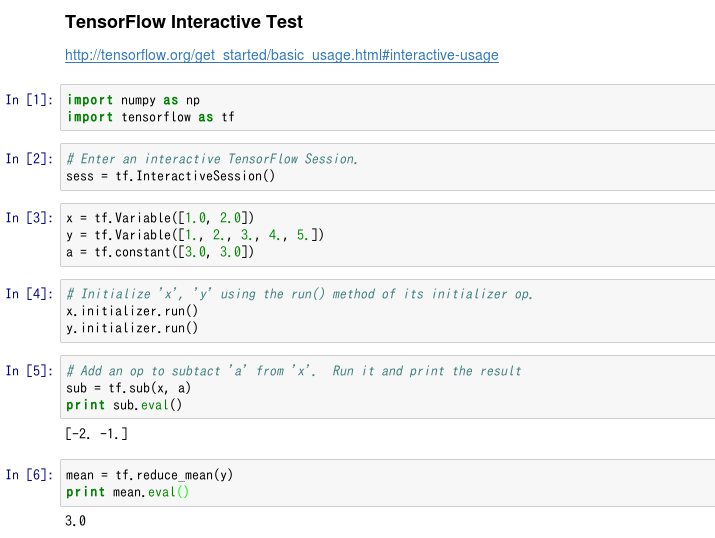
Diese Art der Verwendung scheint praktisch zu sein, wenn Sie von nun an versuchen, TensorFlow zu studieren. (Im Gegenteil, diese interaktive Sitzung eignet sich nicht für die Ausführung eines Programms über einen längeren Zeitraum.)
Logistische Regression
Basierend auf dem obigen linearen Regressionscode haben wir den logistischen Regressionscode erstellt. Beachten Sie, dass dieser Code für die Klassifizierung in zwei Klassen und nicht für die Klassifizierung in mehreren Klassen gilt. (Wie Sie wissen, verwendet MNIST die Softmax-Regression, die das Problem der Klassifizierung mehrerer Klassen (10 Klassen) löst.)
def lin_model(X, w, b):
return X * w + b
w = tf.Variable([0.])
b = tf.Variable([0.])
x = tf.placeholder(tf.float32, shape=(mlen))
y = tf.placeholder(tf.float32, shape=(mlen))
p_1 = lin_model(x, w, b)
x_entropy = tf.nn.sigmoid_cross_entropy_with_logits(p_1, y, name='xentropy')
loss = tf.reduce_mean(x_entropy, name='xentropy_mean')
train_step = tf.train.GradientDescentOptimizer(0.5).minimize(loss)
Bei der linearen Regression wird die durch den mittleren quadratischen Fehler (MSE) definierte Kostenfunktion in der logistischen Regression durch die Kreuzentropie ersetzt. "Tf.nn.sigmoid_cross_entropy_with_logits ()" in der zweiten Hälfte der obigen Liste ist eine Funktion, die die Kreuzentorpie berechnet. ("TensorFlow" hat viele lange benannte Funktionen ...)
Die Initialisierung der Variablen und die Vorgehensweise bei der Sitzung sind dieselben wie im vorherigen Code.
Bisher haben wir die Codes für lineare Regression und logistische Regression gesehen. An diesem Punkt können wir meiner Meinung nach reibungslos mit der Arbeit an MLP-Code (Multi Layer Perceptron) (z. B. MNIST) beginnen.
Referenzen (Website)
- TensorFlow web site http://www.tensorflow.org/
- Newmu Theano-Tutorials - GitHub https://github.com/Newmu/Theano-Tutorials
- Versuchen Sie eine Regression mit TensorFlow - Qiita http://qiita.com/syoamakase/items/db883d7ebad7a2220233
- Genießen Sie Coursera / Materialien für maschinelles Lernen zweimal - Qiita http://qiita.com/TomokIshii/items/b22a3681cb17836c8f6e
(Hinweis) Das TenforFlow-Dokument scheint häufig aktualisiert zu werden, wahrscheinlich weil die Version noch flach ist. Bitte vergib mir, wenn der Link defekt ist.