 | Einführung in die Computerphysik
(2000 / 12)
Harvey Gold, Jant Bochinik usw.
Produktdetails anzeigen
Wird bezeichnet.
Viele Dinge, die durch zufälliges Hinzufügen von Grundeinheiten zur natürlichen Welt wachsen, wie die Bildung blitzförmiger Risse in Schneekristallen und geologischen Verwerfungen sowie das Wachstum von Bakterienkolonien, können beobachtet werden. Eines der bekannten Modelle ist die Diffusion-Limited Aggregation (DLA). Dieses Modell ist ein Beispiel dafür, wie zufällige Bewegungen schöne selbstähnliche Cluster erzeugen.
Die Schritte des Clusterwachstums sind
- Eine Art von Teilchen nimmt einen Gitterpunkt ein
- Emittieren Sie ein Partikel aus dem Kreis um den Samen
- Gehen Sie die Partikel nach dem Zufallsprinzip
- Wenn Sie einen Punkt um einen erreichen, haftet dieser daran → Weiter mit 2
Wiederholen Sie diesen Vorgang, bis sich ein großer Cluster gebildet hat (normalerweise tausende bis millionenfach). Um den Rechenaufwand zu verringern, entfernen wir in Schritt 3 die Partikel, die zu weit vom Cluster entfernt sind, und beginnen erneut mit Schritt 2.
Um diese Operation tatsächlich zu realisieren, müssen wir nur eine Matrix haben, die das Gitter darstellt, und ein Array, das die Punkte um die belegten Gitterpunkte aufzeichnet. Der Teil des Zufallslaufs wird viele Male umgeleitet, erzeugt jedoch eine einheitliche Zufallszahl und bestimmt die Richtung von oben, unten, links und rechts durch die Größe des Werts. In der eigentlichen Simulation nimmt der Zufallslauf an einer Position weit vom Cluster entfernt den größten Teil der CPU-Zeit in Anspruch und wird ineffizient. Versuchen Sie daher, die Schrittlänge des Zufallslaufs an einer Position weit vom Cluster zu erhöhen. Es war. Wir haben die eigentliche Simulation erfasst (Erstellen eines Clusters für N = 200, 500, 1000), die unten bestätigt werden kann.
http://youtu.be/qLii4DlBnv0
Ich habe nichts bearbeitet, also ist es hässlich, aber w
a, b, c bedeuten a, b, c des Lehrbuchproblems, und a erstellt einen Cluster mit der im Eingabefeld angegebenen Anzahl von Partikeln. b und c dienen zum Ermitteln der Adhäsionswahrscheinlichkeit durch Monte-Carlo-Simulation und zum tatsächlichen Ermitteln der fraktalen Dimension. Bei Interesse lesen Sie bitte den Quellcode.
Die bei N = 500 erhaltenen Cluster sind wie folgt.
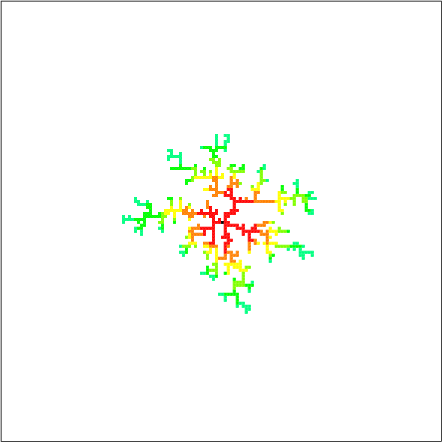
Link ( Einfaches chemisches Experiment - Erstellen eines schönen Silberbaums </ strong> Glaubst du nicht, es sieht dem Bild von Ginju in a>) sehr ähnlich? Da zufällige Spaziergänge der Diffusion entsprechen, kann gesagt werden, dass die Simulation selbst vollständig auf der Bildung von Metallbäumen basiert und die Formen der resultierenden Figuren natürlich sehr ähnlich sind.
Der Quellcode ist unten aufgeführt.
Die Funktion pr zum Speichern von Canvas wird in Zukunft wahrscheinlich häufig verwendet. SetParameter ist auch eine der Klassen, die ich seit langer Zeit benutze. Ich würde es gerne noch etwas zusammenfassen, aber ich habe im Moment keine Probleme damit, also denke ich, dass ich es noch eine Weile weiter verwenden werde.
DLA.py
#! /usr/bin/env python
# -*- coding:utf-8 -*-
#
# written by ssh0, August 2014.
from Tkinter import *
import numpy as np
import matplotlib.pyplot as plt
import random
import time
class DLA(object):
def __init__(self, N, view=True, color=True):
self.r = 3
self.N = N
self.view = view
self.color = color
self.L = int(self.N**(0.78))
if self.view:
self.default_size = 640 # default size of canvas
self.rsize = int(self.default_size/(2*self.L))
if self.rsize == 0:
self.rsize = 1
fig_size = 2*self.rsize*self.L
self.margin = 10
self.sub = Toplevel()
self.canvas = Canvas(self.sub, width=fig_size+2*self.margin,
height=fig_size+2*self.margin)
self.c = self.canvas.create_rectangle
self.update = self.canvas.update
self.sub.title('DLA cluster')
self.c(self.margin, self.margin,
fig_size+self.margin, fig_size+self.margin,
outline='black', fill='white')
self.canvas.pack()
self.start_time = time.time()
def grow_cluster(self):
lattice = np.zeros([self.L*2+1, self.L*2+1], dtype=int)
#Samengitterpunkte
self.center = self.L
lattice[self.center, self.center] = 1
if self.view:
c = self.c
rect = c((2*self.center-self.L)*self.rsize+self.margin,
(2*self.center-self.L)*self.rsize+self.margin,
(2*(self.center+1)-self.L)*self.rsize+self.margin-1,
(2*(self.center+1)-self.L)*self.rsize+self.margin-1,
outline='black', fill='black')
rn = np.random.rand
def reset():
"""Auswahl des Ausgangspunkts"""
theta = 2*np.pi*rn()
x = int((self.r+2)*np.cos(theta))+self.center
y = int((self.r+2)*np.sin(theta))+self.center
return x, y
x, y = reset()
l = 1
n = 0
while n < self.N:
#Erhöhen Sie den Schritt weit von der Peripherie des Clusters entfernt
r = np.sqrt((x-self.center)**2+(y-self.center)**2)
if r > self.r+2:
l = int(r-self.r-2)
if l == 0: l = 1
else:
l = 1
#Zielloser Spaziergang
p = rn()*4
if p < 1:
x += l
elif p < 2:
x -= l
elif p < 3:
y += l
else:
y -= l
r = np.sqrt((x-self.center)**2+(y-self.center)**2)
#Wiederholen Sie den Vorgang an einem Punkt, der vom Mittelpunkt entfernt ist
if r >= 2*self.r:
x, y = reset()
continue
judge = np.sum(lattice[x-1,y]+lattice[x+1,y]
+lattice[x,y-1]+lattice[x,y+1])
#Bringen Sie Partikel in einen Cluster
if judge > 0:
lattice[x, y] = 1
#Zeichnung
if self.view:
if self.color:
colors = ['#ff0000', '#ff8000', '#ffff00', '#80ff00',
'#00ff00', '#00ff80', '#00ffff', '#0080ff',
'#0000ff', '#8000ff', '#ff00ff', '#ff0080']
color = colors[int(n/100)%len(colors)]
else:
color = "black"
rect = c((2*x-self.L)*self.rsize+self.margin,
(2*y-self.L)*self.rsize+self.margin,
(2*(x+1)-self.L)*self.rsize+self.margin-1,
(2*(y+1)-self.L)*self.rsize+self.margin-1,
outline=color, fill=color)
self.update()
#rmax update
if int(r)+1 > self.r:
self.r = int(r) + 1
x, y = reset()
n += 1
else:
if self.view:
self.end_time = time.time()
t = self.end_time-self.start_time
print "done; N = %d, time = " % self.N + str(t) + ' (s)'
return lattice
class SetParameter():
def show_setting_window(self, parameters, commands):
""" Show a parameter setting window.
parameters: A list of dictionaries {'parameter name': default_value}
commands: A list of dictionary {'name of button': command}
"""
self.root = Tk()
self.root.title('Parameter')
frame1 = Frame(self.root, padx=5, pady=5)
frame1.pack(side='top')
self.entry = []
for i, parameter in enumerate(parameters):
label = Label(frame1, text=parameter.items()[0][0] + ' = ')
label.grid(row=i, column=0, sticky=E)
self.entry.append(Entry(frame1, width=10))
self.entry[i].grid(row=i, column=1)
self.entry[i].delete(0, END)
self.entry[i].insert(0, parameter.items()[0][1])
self.entry[0].focus_set()
frame2 = Frame(self.root, padx=5, pady=5)
frame2.pack(side='bottom')
self.button = []
for i, command in enumerate(commands):
self.button.append(Button(frame2, text=command.items()[0][0],
command=command.items()[0][1]))
self.button[i].grid(row=0, column=i)
self.root.mainloop()
class Main(object):
def __init__(self):
import sys
self.sp = SetParameter()
self.dla = None
self.b = None
self.sp.show_setting_window([{'N': 200}],
[{'a': self.exp_a},
{'b': self.exp_b},
{'c': self.exp_c},
{'c:fit': self.fitting},
{'save': self.pr},
{'quit': sys.exit}])
def exp_a(self):
self.N = int(self.sp.entry[0].get())
self.dla = DLA(self.N)
lattice = self.dla.grow_cluster()
def exp_b(self):
trial = 3000
self.dla2 = DLA(2, view=False)
self.dla2.L = 6
distribution = {'p': 0, 'q': 0, 'r': 0, 's': 0}
#Einstufung
for i in range(trial):
lattice = self.dla2.grow_cluster()
l = lattice[self.dla2.L-1:self.dla2.L+2,
self.dla2.L-1:self.dla2.L+2]
if np.sum(l) == 2:
distribution['r'] += 1
elif np.sum(l[0,1]+l[1,0]+l[1,2]+l[2,1]) == 1:
distribution['p'] += 1
elif max(max(np.sum(l, 0)), max(np.sum(l, 1))) == 3:
distribution['s'] += 1
else:
distribution['q'] += 1
for k, v in distribution.items():
distribution[k] = float(v)/trial
distribution['p'] = distribution['p']/2.
distribution['q'] = distribution['q']/2.
print 'trial = %d' % trial
print distribution
def exp_c(self):
self.N = int(self.sp.entry[0].get())
self.dla3 = DLA(self.N, view=False)
self.lattice = self.dla3.grow_cluster()
self.view_expansion()
self.plot()
def view_expansion(self):
lattice = self.lattice
center = self.dla3.center
M_b = []
s = np.sum
ave = np.average
append = M_b.append
for k in range(1, center):
nonzero = np.nonzero(lattice[k:-k,k:-k])
tmp = np.array([0])
for i, j in zip(nonzero[0]+k, nonzero[1]+k):
tmp = np.append(tmp, s(lattice[i-k:i+k+1, j-k:j+k+1]))
append(ave(tmp))
self.b = np.array([2.*k+1 for k in range(1, center)])
self.M_b = np.array(M_b)
def plot(self):
fig = plt.figure("Fractal Dimension")
self.ax = fig.add_subplot(111)
self.ax.plot(self.b, self.M_b, '-o')
self.ax.set_xlabel(r'$b$', fontsize=16)
self.ax.set_ylabel(r'$M(b)$', fontsize=16)
self.ax.set_xscale('log')
self.ax.set_yscale('log')
self.ax.set_ymargin(0.05)
fig.tight_layout()
plt.show()
def fitting(self):
if self.b == None:
return
import scipy.optimize as optimize
def fit_func(parameter0, b, M_b):
log = np.log
c1 = parameter0[0]
c2 = parameter0[1]
residual = log(M_b) - c1 - c2*log(b)
return residual
def fitted(b, c1, D):
return np.exp(c1)*(b**D)
cut_from = int(raw_input("from ? (index) >>> "))
cut_to = int(raw_input("to ? (index) >>> "))
cut_b = np.array(list(self.b)[cut_from:cut_to])
cut_M_b = np.array(list(self.M_b)[cut_from:cut_to])
parameter0 = [0.1, 2.0]
result = optimize.leastsq(fit_func, parameter0, args=(cut_b, cut_M_b))
c1 = result[0][0]
D = result[0][1]
self.ax.plot(cut_b, fitted(cut_b, c1, D),
lw=2, label="fit func: D = %f" % D)
plt.legend(loc='best')
plt.show()
def pr(self):
import tkFileDialog
import os
if self.dla is None:
print "first you should run 'a'."
return
fTyp=[('eps flle','*.eps'), ('all files','*')]
filename = tkFileDialog.asksaveasfilename(filetypes=fTyp,
initialdir=os.getcwd(),
initialfile="figure_1.eps")
if filename == None:
return
self.dla.canvas.postscript(file=filename)
if __name__ == '__main__':
Main()
|

