Hauptkomponentenanalyse (PCA) und unabhängige Komponentenanalyse (ICA) mit Python

Einführung

Bei der Analyse von Gehirnwellen- (EEG) und Enzephalogrammdaten (MEG) in der Forschung haben wir uns entschieden, PCA und ICA zu verwenden, um die Komponenten der Gehirnaktivität zu zerlegen und die Ergebnisse der Dimensionsreduktion als Merkmalsgrößen zu analysieren. Um ehrlich zu sein, bin ich mir über den mathematischen Hintergrund nicht sicher, aber vorerst habe ich die PCA und ICA von Zeitreihendaten als Memorandum auf Implementierungsbasis zusammengefasst.

• Ich hoffe, später einen mathematischen Hintergrund hinzufügen zu können.

Hauptkomponentenanalyse (PCA) und unabhängige Komponentenanalyse (ICA)

Was ist PCA?

Wikipedia Als,

• Die Hauptkomponentenanalyse (PCA) ist eine multivariate Analyse, bei der eine Variable namens Hauptkomponente synthetisiert wird, die die Gesamtvariation mit einer kleinen Anzahl nicht korrelierter Variablen aus einer großen Anzahl korrelierter Variablen am besten darstellt. Eine Methode. Wird verwendet, um die Dimension von Daten zu reduzieren. Die Transformation, die die Hauptkomponente ergibt, wird ausgewählt, um die Dispersion der ersten Hauptkomponente zu maximieren und die Dispersion unter der Bedingung zu maximieren, dass die nachfolgenden Hauptkomponenten orthogonal zu den zuvor bestimmten Hauptkomponenten sind. * *

Mit anderen Worten ** Wenn davon ausgegangen werden kann, dass die Daten einer Normalverteilung folgen, die Methode, die Achse in orthogonaler Richtung in der Reihenfolge von der Komponente mit der größten Streuung zu nehmen Da die Basen orthogonal sind, sind die Ausgaben nicht korrelierte Daten miteinander (es gibt keine lineare Beziehung, aber möglicherweise eine nichtlineare Beziehung) **

Was ist ICA?

[Wikipedia](https://ja.wikipedia.org/wiki/%E7%8B%AC%E7%AB%8B%E6%88%90%E5%88%86%E5%88%86%E6%9E Ab% 90 "Wikipedia")

• Die unabhängige Komponentenanalyse (ICA) ist eine Berechnungsmethode zur Trennung multivariater Signale in mehrere additive Komponenten. Jede Komponente nimmt ein nicht unabhängig voneinander Gaußsches Signal an. Dies ist ein Sonderfall der blinden Signaltrennung. * *

Mit anderen Worten ** Eine Methode, die in Richtung maximaler Unabhängigkeit zeigt, wenn davon ausgegangen werden kann, dass die Daten statistisch unabhängig sind und keiner Normalverteilung folgen. Die Ausgabe besteht aus unabhängigen Daten, die keiner Normalverteilung folgen (keine linearen oder nichtlinearen Beziehungen) **

Unterschied zwischen PCA und ICA (Bild)

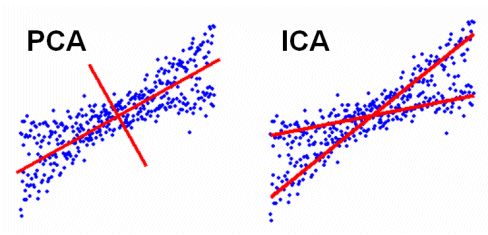(Referenz http://meg.aalip.jp/ICA/)

PCA-Implementierung

PCA.py

import numpy as np
import matplotlib.pyplot as plt

from sklearn.decomposition import PCA
X = input_data #400 (Anzahl der Daten) x 300 (Zeitreihen) Daten

#Führen Sie PCA aus
pca = PCA(n_components=20, random_state=0)#Bilden Sie 20 Basen (Komponenten)
feature = pca.fit_transform(X)
PCA_comp =  pca.components_ #Basismatrix

#Stellen Sie die 0. Daten mit 20 Komponenten wieder her
plt.figure(figsize = (12, 2))
plt.plot(X[0], label="data")#0. Daten
plt.plot(np.dot(feature[0], PCA_comp).T, label="reconstruct")#Wiederhergestellte 0. Daten
plt.legend()

ICA-Implementierung

ICA.py

import numpy as np
import matplotlib.pyplot as plt

from sklearn.decomposition import FastICA
X = input_data #400 (Anzahl der Daten) x 300 (Zeitreihen) Daten

#Implementierung von ICA
ICA = FastICA(n_components=20, random_state=0)#Bilden Sie 20 Basen (Komponenten)
X_transformed = ICA.fit_transform(X)
A_ =  ICA.mixing_.T #Gemischte Matrix

#Stellen Sie die 0. Daten mit 20 Komponenten wieder her
plt.figure(figsize = (12, 2))
plt.plot(X[0], label="data")#0. Daten
plt.plot(np.dot(X_transformed[0], A_), label="reconstruct")#Wiederhergestellte 0. Daten
plt.legend()

abschließend

Dieses Mal habe ich PCA und ICA als Memorandum zusammengefasst. Ich dachte, es wäre in Ordnung, weil ich es vorerst implementieren konnte, aber ich denke, ich muss mehr theoretisches Wissen für die Zukunft erwerben. Ich möchte etwas über NMF (Non-Negative Matrix Factor Decomposition) hinzufügen.

Referenz

・ Dimensionsreduktionsmethode (Zusammenfassung und Implementierung) PCA, LSI (SVD), LDA, ICA