[PYTHON] Verwenden Sie die Kombinationsoptimierung
Einführung
Ich werde das Know-how für die Verwendung der Kombinationsoptimierung erläutern.
Der Trick bei der Verwendung der Kombinationsoptimierung besteht darin, das Gesamtbild zu erhalten. Wenn Sie wissen, was die Elemente sind und in welcher Beziehung sie zueinander stehen, können Sie sich dem Problem nähern, das Sie lösen möchten. Mit Python können Sie problemlos verschiedene Optimierungen vornehmen. Lassen Sie es uns später überprüfen, während Sie sich den tatsächlichen Code ansehen. Schauen wir uns zunächst ein Beispiel für eine bekannte Optimierung an.
Denken wir nach
Neulich, als Sie nach Hause zurückkehrten, wurde Ihnen gesagt, Sie sollten Gemüse als Souvenir mitbringen. Das Gemüse in Tokio ist teuer, deshalb war ich erfreut, dass es "rentabel" war, aber die Menge war zu groß. Angenommen, Sie können höchstens 5 kg zurückbringen. (Bitte keinen Kurier benutzen) Außerdem wird das Gemüse beim Schneiden beschädigt, sodass ich es so wie es ist mit nach Hause nehmen kann.
Sie dachten: "Wählen wir aus denen mit dem höchsten Verkaufspreis pro kg." Tatsächlich ist dies nicht die beste Methode (obwohl es sich um eine schnelle und gute Näherungslösung handelt, die als gierige Methode bezeichnet wird) (http://qiita.com/Tsutomu-KKE@github/items/ce0d17b15a0226c94a0e). Woher kennst du den wirklich besten Weg?
Wenn Sie sich alle Möglichkeiten ansehen, wissen Sie, wie Sie optimieren können. Alle Gemüsekombinationen explodieren jedoch mit zunehmender Anzahl von Gemüse und können nicht berechnet werden. ** Mathematische Optimierung ** kann verwendet werden, um solche Probleme zu lösen. Die mathematische Optimierung verwendet mathematische Formeln, um das Problem mit einem ** mathematischen Modell ** darzustellen. Das vorherige Beispiel ist
| Maximieren | $ \ sum_i {p_i x_i} $ | $ p_i $: Verkaufspreis weniger |
| $ \ forall x_i \ in \ {0, 1 \} $ | $ x_i $: Gibt an, ob es nach Hause gebracht werden soll > |
| Kontinuierliche Optimierung: | Nur kontinuierliche Elemente |
| Kombinationsoptimierung: | Enthält nicht kontinuierliche diskrete Elemente |
Formulierung
Lektion 1
** Bei der Kombinationsoptimierung wird ein mathematisches Modell formuliert. ** **.
Um zu formulieren, müssen wir drei Faktoren bestimmen.
| 1. Was möchten Sie entscheiden? | "Ich möchte entscheiden, welches Gemüse zurückgebracht werden soll" |
| 2. Was möchten Sie tun? | "Ich bin froh, wenn der Gesamtverkaufspreis des zurückgebrachten Gemüses höher ist" |
| 3. Was muss ich schützen? | "Wiegen Sie weniger als 5 kg Gemüse, um es zurückzubringen" |
| 1. Variablen: | $ \ forall x_i \ in \ {0, 1 \} $ | |
| 2. Zielfunktion: | $ \ sum_i {p_i x_i} $ | $ \ rightarrow $ maximum |
| 3. Einschränkungen: | $ \ sum_i {w_i x_i} \ le 5 $ |
Es ist gewöhnungsbedürftig, um formulieren zu können. Dieses Mal werden wir uns später einige Beispiele ansehen. Wenn Sie detailliert studieren möchten, lesen Sie bitte das Buch "Kann ab heute verwendet werden! Kombinationsoptimierung". Verwenden Sie ein Werkzeug (von einem Weisen erstellt), um die beste Antwort aus einem mathematischen Modell zu finden. Dieses Tool wird als optimierter Löser oder kurz ** Löser ** bezeichnet. Mit anderen Worten, Sie können das Problem einfach darstellen (damit jeder es verstehen kann) und mit dem Löser eine Lösung finden (die Antwort). Heutzutage ist dieser Solver einfach zu bedienen und seine Leistung hat sich stark verbessert. Jeder fängt an, die Optimierung zu versuchen.
Typisches Problem
Welche anderen Beispiele gibt es neben den vorherigen? Möglicherweise haben Sie bei Ihrer Rückkehr nach Hause im Internet nach einer Übergabestation gesucht.
Ich möchte die kürzeste (oder billigste) Route vom Bahnhof in Ihrer Nähe zum Bahnhof in der Nähe Ihres Elternhauses finden.
Dies ist auch ein Optimierungsproblem. An vielen Stellen gibt es viele Optimierungsprobleme. Es ist jedoch schwierig, jedes Problem zu formulieren. In der Tat haben verschiedene Probleme oft die gleiche Formulierung. Auf diese Weise müssen Sie sich nicht die Mühe machen, es zu formulieren, was praktisch ist. Wir werden die allgemeinen Probleme der Welt als ** typische Probleme ** bezeichnen.
Lektion 2
** Typische Probleme verstehen. ** **.
Sammeln Sie verwandte typische Probleme und erstellen Sie ein Framework mit dem Namen ** typische Problemklasse **. Es gibt sieben typische Problemklassen. Für typische Probleme haben wir die am häufigsten verwendeten sorgfältig ausgewählt.
| Typische Problemklasse | Typisches Problem |
| Grafiknetzwerkproblem | Minimales Problem des gesamten Flächenbaums |
| Problem mit maximaler stabiler Menge | |
| Maximales Schnittproblem | |
| Problem der minimalen Scheitelpunktabdeckung | |
| Problem mit der kürzesten Route | |
| Problem mit maximalem Durchfluss | |
| Problem des minimalen Kostenflusses | |
| Routenproblem | Transportroutenproblem |
| Patrol Salesman Problem | |
| Problem der aggregierten Abdeckung / Teilung | Problem der aggregierten Abdeckung |
| Problem der Gruppenaufteilung | |
| Planungsproblem | Job-Shop-Problem |
| Arbeitsplanungsproblem | |
| Problem mit Aussparung / Störung | Rucksackproblem |
| Problem beim Verpacken des Behälters | |
| n-dimensionales Packungsproblem | |
| Platzierungsproblem | Platzierungsproblem der Einrichtung |
| Keine Kapazitätsbeschränkung Problem bei der Platzierung der Einrichtung | |
| Zuordnungs- / Übereinstimmungsproblem | Sekundäres Zuordnungsproblem |
| Allgemeines Zuordnungsproblem | |
| Maximales Übereinstimmungsproblem | |
| Gewichtsanpassungsproblem | |
| Stabiles Übereinstimmungsproblem |
Die Auswahl von Gemüse wird als ** Rucksackproblem ** bezeichnet, und die Suche nach Transferstationen wird als ** Problem mit der kürzesten Route ** bezeichnet. Typische Probleme sind gut untersucht und haben oft effiziente Lösungen. Alternativ ist es so formuliert, dass es sofort gelöst werden kann. Lass es uns später tun. Beispiele zur Ausführung aller hier aufgeführten typischen Probleme finden Sie unter Typische Probleme und Ausführungsmethoden.
Allgemeines Problem
Ich werde über die Containerarbeit sprechen, die ich in letzter Zeit mache. Dank des Containertransports können Menschen auf der ganzen Welt verschiedene Dinge billig kaufen. Dies liegt daran, dass in China hergestellte Produkte in großen Mengen zu niedrigen Preisen nach Japan, in die USA und nach Europa geliefert werden können. Leere Behälter stapeln sich jedoch immer mehr. Ich muss wieder nach China zurück. Die Bestimmung, wann, wo und wohin zurückgegeben werden soll, ist das ** Problem des minimalen Kostenflusses **. Es gibt jedoch einige Einschränkungen, die nicht durch das Problem des minimalen Kostenflusses ausgedrückt werden können. Einer heißt Kabotage. Kabotage regelt den Inlandstransport nur zu inländischen Unternehmen. Wenn das typische Problem nicht gelöst werden kann, wird das mathematische Modell so behandelt, wie es ist. Das durch das mathematische Modell dargestellte Problem heißt ** allgemeines Problem **. Typische Probleme können auch als Allzweckprobleme angesehen werden. Allzweckprobleme sind eine allgemeinere Klassifizierung als typische Probleme.
Lektion 3
** Allgemeine Probleme verstehen. ** **.
Was sind die allgemeinen Probleme?
Unterschiede bei allgemeinen Problemen sind auf Unterschiede bei Variablen, Zielfunktionen und Einschränkungen zurückzuführen. Unterschiedliche Allzweckprobleme haben unterschiedliche Lösungen (Algorithmen). Die einfache Lösung ist je nach Art dieser Lösung völlig unterschiedlich. Außerdem kann jedes generische Problem einen anderen Löser haben. Es ist so wichtig wie möglich, es zu einem allgemeinen Problem zu bringen, das leicht gelöst werden kann. Das allgemeine Problem ist eine Eltern-Kind-Beziehung.

Alle Optimierungsprobleme sind nichtlineare Optimierungsprobleme. Warum sich mit nichtlinearer Optimierung beschäftigen? Dies liegt daran, dass es ineffizient ist, das Problem der linearen Optimierung als nichtlineare Optimierung zu behandeln. Der Begriff nichtlineare Optimierung legt implizit nahe, dass es eine nichtlineare Zielfunktion oder eine nichtlineare Einschränkung gibt.
** Lineares Optimierungsproblem **
Das am einfachsten zu lösende Allzweckproblem ist das lineare Optimierungsproblem. Das Problem des minimalen Kostenflusses und das Problem der kürzesten Route sind ebenfalls lineare Optimierungsprobleme. Dies ist ein Problem, bei dem die Variable eine kontinuierliche Variable ist und die Zielfunktion und die Randbedingung linear ausgedrückt werden (linearer Ausdruck). Dies ist in der Lage, auch ziemlich große Probleme zu lösen.
** Optimierungsproblem mit gemischten Ganzzahlen **
Die Zielfunktion und die Einschränkungen sind linear, aber Probleme, die ganzzahlige Variablen (nur Ganzzahlen sind zulässig) in den Variablen enthalten, werden als Optimierungsprobleme für gemischte Ganzzahlen bezeichnet. Das Rucksackproblem ist auch ein Optimierungsproblem für gemischte Ganzzahlen. Dies ist ein häufiges Problem in der Praxis und viele der Probleme, mit denen ich mich befasse. Es ist ein schwieriges Problem, aber in letzter Zeit ist es möglich geworden, es abhängig von der Formulierung und dem Ausmaß des Problems zu lösen. "Wir sind jetzt in der Lage, gemischte ganzzahlige Optimierungsprobleme zu lösen." Aus diesem Grund wurde der Optimierungsschwellenwert gesenkt. Für Anfänger in der mathematischen Optimierung besteht ein Ziel darin, ein einfaches Optimierungsproblem für gemischte Ganzzahlen zu formulieren. In der Praxis kann der Umgang mit Optimierungsproblemen mit gemischten Ganzzahlen jedoch schwierig sein und einen gewissen Einfallsreichtum erfordern.
** Nichtlineares Optimierungsproblem **
Die nichtlineare Optimierung ist ein noch schwierigeres Problem. Wenn es sich jedoch um einen kleinen Maßstab handelt, kann es auch derzeit noch gelöst werden. Bei der nichtlinearen Optimierung kann die nichtlineare konvexe Optimierung auch in großem Maßstab durchgeführt werden, wird hier jedoch weggelassen.
Wir werden diese drei Beispiele später sehen.
Beziehung zwischen typischen Problemen und allgemeinen Problemen
Alle mathematischen Optimierungsprobleme sind entweder Allzweckprobleme. Allzweckprobleme können als eine Hauptkategorie von Kombinationsoptimierungsproblemen angesehen werden. Diese Klassifizierung ist jedoch zu grob. Die Klassifizierung von Organismen erfolgt wie bei Wirbeltieren und Wirbellosen. Ein typisches Problem kann als Unterklasse angesehen werden. Sind sie in Bezug auf Lebewesen Insekten und Säugetiere? Es wird einfacher sein, sich zu erinnern, weil Sie das typische Problem genauer spüren können.

- Eine typische Problemklasse kann verschiedene generische Probleme enthalten. ――Die Formulierung kann als Designzeichnung bezeichnet werden, die der DNA in lebenden Organismen ähnelt. Obwohl ein Organismus nur eine DNA hat, kann ein Problem als separates Problem angesehen werden. ――Der Löser (dh die Lösung) ändert sich je nachdem, wie Sie ihn als Allzweckproblem oder als typisches Problem betrachten.
- Im Allgemeinen sind typische Problemlöser effizienter als allgemeine Problemlöser.

Ich werde das allgemeine Problem ergänzen. Obwohl Wirbeltiere und Wirbellose in lebenden Organismen getrennte Gruppen sind, beziehen sie sich grundsätzlich auf die Klassifizierung allgemeiner Probleme. Das heißt, alle Probleme sind nichtlineare Optimierungsprobleme, darunter gemischte ganzzahlige Optimierungsprobleme, und unter ihnen sind lineare Optimierungsprobleme. Mit anderen Worten ist das lineare Optimierungsproblem sowohl ein gemischtes ganzzahliges Optimierungsproblem als auch ein nichtlineares Optimierungsproblem. Das gemischte ganzzahlige Optimierungsproblem ist auch ein nichtlineares Optimierungsproblem. Dies gilt auch beim Anwenden von Lösern. Das heißt, der nichtlineare Optimierungslöser kann alle nichtlinearen Optimierungsprobleme, gemischte ganzzahlige Optimierungsprobleme und lineare Optimierungsprobleme behandeln. Der Löser für die Optimierung gemischter Ganzzahlen kann keine allgemeinen nichtlinearen Optimierungsprobleme behandeln, kann jedoch Optimierungsprobleme gemischter Ganzzahlen und lineare Optimierungsprobleme behandeln. Der Linear Optimization Solver kann nur Probleme mit der linearen Optimierung lösen. Herkömmlicherweise werden gemischte ganzzahlige Optimierungslöser und lineare Optimierungslöser häufig zu einem Löser kombiniert.
Einige nichtlineare Optimierungslöser können und können Einschränkungen nicht berücksichtigen. Für Praktiker scheint es jedoch ausreichend zu sein, sich nur um Löser zu kümmern, die Einschränkungen berücksichtigen können. Daher gehen wir hier davon aus, dass Einschränkungen berücksichtigt werden können. Ich bin.
Solver arbeiten in kleineren Bereichen besser. Bei linearen Optimierungsproblemen ist es mit dem linearen Optimierungslöser schneller, die optimale Lösung zu erhalten. Die Verwendung eines nichtlinearen Optimierungslösers für ein lineares Optimierungsproblem hat Nachteile wie "Es ist erforderlich, eine anfängliche Lösung anzugeben" und "Es dauert sehr viel Rechenzeit".
Unter Optimierungsforschern gibt es eine viel feinere Klassifizierung, aber für viele Praktiker sind drei Typen ausreichend: nichtlineare Optimierung, gemischte Ganzzahloptimierung und lineare Optimierung. Das Optimierungsproblem für gemischte Ganzzahlen wird auch als lineares Optimierungsproblem für gemischte Ganzzahlen bezeichnet. Die Forscher nennen lineare Optimierung LP (lineare Programmierung), gemischte ganzzahlige Optimierung MIP oder MILP (gemischte ganzzahlige lineare Programmierung) und nichtlineare Optimierung NLP (nicht lineare Programmierung). Die Programmierung wurde ursprünglich als "Planung" übersetzt, aber seit kurzem wird sie als Optimierung bezeichnet. Deshalb haben wir sie auch hier mit der Optimierung vereinheitlicht. Da Optimierung Optimierung ist, kann sich die Art und Weise, wie sie genannt wird, in Zukunft ändern.
Beispiel für die Ausführung eines typischen Problems mit Python
Lektion 4
** Lass es uns versuchen. ** **.
** Rucksackproblem **
Packen Sie etwas Gepäck in den Rucksack. Maximieren Sie die Summe der Gewichte des Gepäcks so, dass die Summe der Größen des zu verpackenden Gepäcks die Kapazität des Rucksacks nicht überschreitet.
python
from ortoolpy import knapsack
size = [21, 11, 15, 9, 34, 25, 41, 52]
weight = [22, 12, 16, 10, 35, 26, 42, 53]
capacity = 100
knapsack(size, weight, capacity)
>>>
(105, [0, 1, 3, 4, 5])
Sie erhalten die Summe der Werte der ausgewählten Pakete (105) und der Reihenfolge der ausgewählten Pakete ([0, 1, 3, 4, 5]).
** Kürzestes Straßenproblem **
Suchen Sie in der Grafik die kürzeste Route vom Startpunkt zum Endpunkt.
python
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1)
nx.dijkstra_path(g, 0, 2)
>>>
[0, 1, 6, 3, 5, 2]
Erstellen Sie ein zufälliges Diagramm mit 8 Punkten, um eine Liste der kürzesten Pfade von Knoten 0 zu Knoten 2 zu erhalten ([0, 1, 6, 3, 5, 2]).
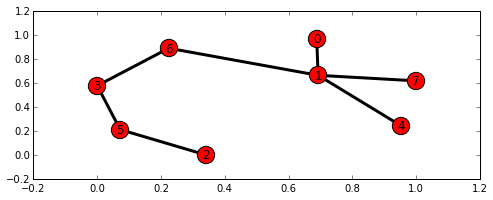
Weitere typische Beispiele für die Problemausführung finden Sie unter Typische Probleme und Ausführungsmethoden.
Beispiel für die Ausführung eines allgemeinen Problems mit Python
Informationen zur Verwendung von PuLP finden Sie unter [Erstellen eines allgemeinen Problems mit PuLP](# Zellstoff% E3% 81% A7% E3% 81% AE% E6% 95% B0% E7% 90% 86% E5% 95% 8F% E9 Wir verweisen auf% A1% 8C% E3% 81% AE% E4% BD% 9C% E3% 82% 8A% E6% 96% B9).
** Rucksackproblem **
Packen Sie etwas Gepäck in den Rucksack. Maximieren Sie die Summe der Gewichte des Gepäcks so, dass die Summe der Größen des zu verpackenden Gepäcks die Kapazität des Rucksacks nicht überschreitet.
python
from pulp import *
size = [21, 11, 15, 9, 34, 25, 41, 52]
weight = [22, 12, 16, 10, 35, 26, 42, 53]
capacity = 100
r = range(len(size))
m = LpProblem(sense=LpMaximize) #Mathematisches Modell
x = [LpVariable('x%d'%i, cat=LpBinary) for i in r] #Variable
m += lpDot(weight, x) #Zielfunktion
m += lpDot(size, x) <= capacity #Zwang
m.solve()
print((value(m.objective), [i for i in r if value(x[i]) > 0.5]))
>>>
(105.0, [0, 1, 3, 4, 5])
Das Rucksackproblem ist ein gemischtes ganzzahliges Optimierungsproblem für allgemeine Probleme.
** Kürzestes Straßenproblem **
Suchen Sie in der Grafik die kürzeste Route vom Startpunkt zum Endpunkt.
python
from pulp import *
import networkx as nx
g = nx.fast_gnp_random_graph(8, 0.26, 1).to_directed()
source, sink = 0, 2 #Startpunkt,Endpunkt
r = list(enumerate(g.edges()))
m = LpProblem() #Mathematisches Modell
x = [LpVariable('x%d'%k, lowBound=0, upBound=1) for k, (i, j) in r] #Variable(Ob man die Straße betritt)
m += lpSum(x) #Zielfunktion
for nd in g.nodes():
m += lpSum(x[k] for k, (i, j) in r if i == nd) \
== lpSum(x[k] for k, (i, j) in r if j == nd) + {source:1, sink:-1}.get(nd, 0) #Zwang
m.solve()
print([(i, j) for k, (i, j) in r if value(x[k]) > 0.5])
>>>
[(0, 1), (1, 6), (3, 5), (5, 2), (6, 3)]
Das Problem mit dem kürzesten Weg ist ein lineares Optimierungsproblem für allgemeine Probleme. Für das Problem des kürzesten Weges gibt es eine effiziente Lösung, die als Dyxtra-Methode bezeichnet wird. Es wird nicht empfohlen, es als Allzweckproblem zu lösen. Die Dyxtra-Methode ist [Beispiel für die Ausführung eines typischen Problems durch Python](# python-% E3% 81% AB% E3% 82% 88% E3% 82% 8B% E6% A8% 99% E6% BA% 96% E5% Es wird im Beispiel (nx.dijkstra_path) von 95% 8F% E9% A1% 8C% E3% 81% AE% E5% AE% 9F% E8% A1% 8C% E4% BE% 8B verwendet.
** Portfoliooptimierungsproblem **
Bestimmen Sie den Prozentsatz ($ x_i
), um die Aktie zu kaufen. Minimieren Sie das Risiko (Diversifikation ( v_i $)) vorbehaltlich der Untergrenze der Kapitalrendite (t / Yen). Jedes Problem ist jedoch unabhängig.
python
import numpy as np, scipy.optimize as so
p = [31, 86, 29, 73, 46, 39, 58] #Profitieren/Kreis
v = [10, 60, 25, 50, 35, 30, 40] #Verteilt/Kreis
t = 50 #Zielgewinn/Kreis
so.fmin_slsqp(lambda x: sum(v*x*x), np.zeros(len(p)),
eqcons=[lambda x: sum(x) - 1], ieqcons=[lambda x: sum(p*x) - t])
>>>
Optimization terminated successfully. (Exit mode 0)
Current function value: 4.50899167487
Iterations: 14
Function evaluations: 136
Gradient evaluations: 14
array([ 0.26829785, 0.13279566, 0.09965076, 0.1343941 , 0.11783349,
0.11506705, 0.13196109])
Das Portfoliooptimierungsproblem ist ein nichtlineares Optimierungsproblem für allgemeine Probleme.
Grafiknetzwerk
Es gibt viele Probleme mit dem Grafiknetzwerk bei Problemen mit der Kombinationsoptimierung. Es ist wichtig, deshalb werde ich es hier kurz vorstellen. Ein Graph ist eine Struktur, die aus Punkten und Kanten besteht, die die Punkte verbinden. Es wird oft verwendet, um reale Beziehungen auf abstrakte Weise auszudrücken.
$ G = (V, E) $ bedeutet, dass "Graph (G) aus Punktmenge (V) und Kantenmenge (E) besteht". Ein Einwegdiagramm wird als gerichtetes Diagramm bezeichnet, und ein Diagramm mit anderen Seiten wird als ungerichtetes Diagramm bezeichnet. Eine Reihe von Kanten von einem Punkt zum anderen wird als Pfad bezeichnet. Die Verbindung zwischen dem Start- und dem Endpunkt der Route wird als geschlossene Route bezeichnet. Ein Netzwerk ist ein System, das den Fluss von etwas auf der Seite des Diagramms berücksichtigt. Es gibt Straßennetze, Kommunikationsnetze usw.
Software Installation
Wir empfehlen die Verwendung von Anaconda als einfache Installationsmethode. Laden Sie zum Installieren von Anaconda das Installationsprogramm von Site herunter und führen Sie es aus.
Anaconda enthält Python selbst und viele Pakete für wissenschaftliche und technologische Berechnungen. Neben Anaconda ist PuLP, ein Modellierer für mathematische Optimierung, und eine Bibliothek für typische Probleme die erforderliche Software.
--PuLP wird mit "pip install pulp" installiert.
- Die Installation der Bibliothek für typische Probleme ist "pip install or toolpy".
So erstellen Sie ein allgemeines Problem mit PuLP
- Bibliothek importieren
- from pulp import *
- Erstellung eines mathematischen Modells
- Für Minimierungsprobleme: m = LpPrblem ()
- Für Maximierungsprobleme: m = LpProblem (sense = LpMaximize)
- Variablen erstellen
- Kontinuierliche Variable: x = LpVariable (Variablenname, lowBound = 0) --0-1 Variable: x = LpVariable (Variablenname, cat = LpBinary)
- Liste der stetigen Variablen: x = [LpVariable (i-ter Variablenname, lowBound = 0) für i im Bereich (n)]
- Stellen Sie sicher, dass die Variablennamen unterschiedlich sind
- Einstellen der Zielfunktion --m + = Ausdruck
- Hinzufügung von Randbedingungen --m + = Ausdruck == Ausdruck --m + = Ausdruck <= Ausdruck --m + = Ausdruck> = Ausdruck --Beispiel für Ausdruck
- 2 * x + 3 * y - 5 --Sum: lpSum (Liste der Variablen) --Inner Produkt: lpDot (Liste der Koeffizienten, Liste der Variablen)
- Run Solver
- m.solve()
- Werte von Variablen, Ausdrücken und Zielfunktionen --Wert (Variable), Wert (Ausdruck), Wert (m.Objektiv)
Referenz
- Python in Optimierung
- Power of Combination Optimization Solver
- Herr Miyashiros Memo of Integer Planning
Zu beachtende Punkte
Bei der praktischen Verwendung der Optimierung sind einige Dinge zu beachten. Aktuelle Optimierungstechniken können reale Herausforderungen nicht vollständig modellieren. Sie können es nicht lösen, ohne das Modell zu vereinfachen, indem Sie die weniger wichtigen Teile abschneiden.
Daher ist das Ergebnis der Optimierung oft nicht so verwendbar, wie es ist. In diesem Fall ist es wichtig zu überprüfen, ob das Problem vorliegt. Es ist auch wichtig, wie die Ergebnisse angezeigt werden, um das Problem schnell zu finden.
Das Verständnis vertiefen
Hier sind einige Schlüsselwörter für weitere Studien.
- Berechnungsbetrag, Auftragsnotation, Klasse P, Klasse NP
- Operations Research, Modellierung, Meta-Huristic, Dualität, Mitigation Issues, Künstliche Intelligenz, Maschinelles Lernen, Spieltheorie
- Verwandte akademische Gesellschaft
- Operations Research Society
- Angewandte Mathematische Gesellschaft --Optimierungsthemen und Erklärungen
- Mathematisches Feld zur Optimierung der Universität Kyoto (Labor für mathematische Optimierung)
- Mathematisches Modell - Wikipedia
- Modellierung und Optimierung sozialer Systeme - Illustration der Notlage
- Problemlösung und Mathematik-Mathematische Mädchen
- Was ist zu beachten, wenn ein komplexes System mit einem mathematischen Modell "verstanden" wird - Standardmodus
Beiseite
In lebenden Organismen sind die beiden Nomenklaturen von Linne (z. B. Homo sapiens für Menschen) üblich, aber selbst bei der Optimierung kann die Denkweise von Allzweckproblemen und typischen Problemen ähnlich sein.
Der Solver ändert sich je nachdem, ob es sich um ein Allzweckproblem oder ein typisches Problem handelt. Es ist jedoch Sache des Benutzers, eine Auswahl zu treffen. In Zukunft kann es möglich sein, automatisch zu bestimmen. Mit anderen Worten, wenn Sie es dem Löser als Allzweckproblem geben und es analysieren und feststellen, dass es eines der typischen Probleme ist, können Sie automatisch eine effizientere Lösung verwenden.
Kennen Sie Higashi Robo-Kun?
Dies ist ein Forschungsprojekt des Nationalen Instituts für Informatik mit dem Thema "Können Roboter die Universität von Tokio betreten?".
Tatsächlich ähnelt der Optimierungsansatz, der auf typischen Problemen basiert, dem von Torobo-kun. Es geht darum, eine Vielzahl von Problemen als typografische Probleme zu lösen. Wenn man diesen Versuch betrachtet, scheint der Tag zu kommen, an dem es möglich sein wird, Probleme automatisch zu optimieren und zu lösen, indem man das Problem einfach auf Japanisch schreibt.
Aber bis dahin müssen Sie selbst denken und Ihre Hände bewegen. Auf diese Weise lernen Sie nach und nach, wie Sie mit komplexeren Problemen umgehen können.
Recommended Posts