[PYTHON] Zusammenfassung der Zufallszahlengenerierung durch Numpy
Der Python-Standard hat auch ein Modul namens random, aber numpy, das Vektoroperationen ausführen kann, läuft schneller, wenn "eine große Anzahl von Zufallszahlen generiert und einige Verarbeitungsschritte ausgeführt werden". Es gibt auch viele Verteilungsfunktionen.
Einheitliche Zufallszahl
Generieren Sie mit numpy.random.rand () eine einheitliche Zufallszahl von 0 bis 1. Durch Angabe eines Arguments können mehrere Zufallszahlen generiert werden. Wenn Sie den Bereich der Zufallszahlen ändern möchten, können Sie später Vektoroperationen ausführen.
from numpy.random import *
rand() #Generieren Sie eine Zufallszahl von 0 bis 1
rand(100) #Generieren Sie 100 Zufallszahlen von 0 bis 1
rand(10,10) #Generieren Sie eine 10x10-Matrix mit Zufallszahlen von 0 bis 1
rand(100) * 40 + 30 #Generieren Sie 100 Zufallszahlen von 30 bis 70
Zufallszahlen, die einer bestimmten Verteilungsfunktion folgen
Eine beliebige Anzahl von Zufallszahlen kann durch Angabe eines Arguments wie size = (10,10) generiert werden.
from numpy.random import *
"""Standardnormalverteilung. Sogenannter Gaußscher. Randn für Standardnormalverteilung()Wenn Sie den Mittelwert / die Varianz angeben möchten, normal()Wird genutzt."""
randn() #Standardnormalverteilung(Durchschnitt 0,Standardabweichung 1)
randn(10) #Generieren Sie 10 Standardnormalverteilungen
randn(10,10) #10x10 Matrix mit Standardnormalverteilung
normal(50,10) #Normalverteilung mit Mittelwert 50 und Standardabweichung 10
"""Binäre Verteilung. Die Anzahl der Münzen, die durch das Werfen von Münzen mit einer Wahrscheinlichkeit von p n vorangestellt werden können."""
binomial(n=100, p=0.5)
"""Poisson-Verteilung. Verteilung der Häufigkeit, mit der ein selten auftretendes Phänomen über einen längeren Zeitraum beobachtet wird. λ ist der Durchschnitt."""
poisson(lam=10) # λ=Poisson-Verteilung von 10
"""Beta-Distribution. Wird für die konjugierte vorherige Verteilung der Binomialverteilung verwendet."""
beta(a=3, b=5) # a=3, b=Beta-Verteilung von 5
Es gibt viele andere Verteilungen wie χ-Verteilung, Richtungsverteilung, Exponentialverteilung, F-Verteilung, Gammaverteilung, geometrische Verteilung, Gambelverteilung, supergeometrische Verteilung, Laplace-Verteilung, logistische Verteilung, logarithmische Normalverteilung und so weiter. Siehe diese Seite für Details. http://docs.scipy.org/doc/numpy/reference/routines.random.html
ganze Zahl
from numpy.random import *
randint(100) #Generieren Sie eine Ganzzahl von 0 bis 99
randint(30,70) #Generieren Sie eine Ganzzahl von 30 bis 69
randint(0,100,20) #Generieren Sie 20 Ganzzahlen von 0 bis 99
randint(0,100,(5,5)) #Generieren Sie eine 5x5-Matrix mit Ganzzahlen von 0 bis 99
random_integers(100) #Generieren Sie eine Ganzzahl von 1 bis 100
random_integers(30,70) #Generieren Sie eine Ganzzahl von 30 bis 70
Zufällige Extraktion aus der Liste
from numpy import *
city = ["Sapporo","Sendai","Tokyo","Nagoya","Kyoto","Osaka","Fukuoka"]
random.choice(city) #Extrahiere zufällig einen
random.choice(city,10) #Zufällige Extraktion von 10 (mit Duplikation)
random.choice(city,5,replace=False) #Zufällige Extraktion von 5 (keine Vervielfältigung))
#Bei der Gewichtung der Wahrscheinlichkeit
weight = [0.1, 0.1, 0.3, 0.1, 0.1, 0.2, 0.1]
random.choice(city, p=weight) #Extrahieren Sie eine mit der angegebenen Wahrscheinlichkeit
Initialisierung der Zufallszahlengenerierung
Die von Numpy generierte Zufallszahl ist eine Pseudozufallszahl. Wenn Sie also einen festen Startwert angeben, wird jedes Mal dieselbe Zufallszahl generiert. Es wird verwendet, wenn jedes Mal dieselbe Zufallszahl ausgegeben werden soll, z. B. beim Debuggen.
from numpy.random import *
seed(100) #Jede Zahl ist in Ordnung
rand() #Gibt jedes Mal den gleichen Wert zurück
Überprüfen Sie die Verteilung mit einem Histogramm
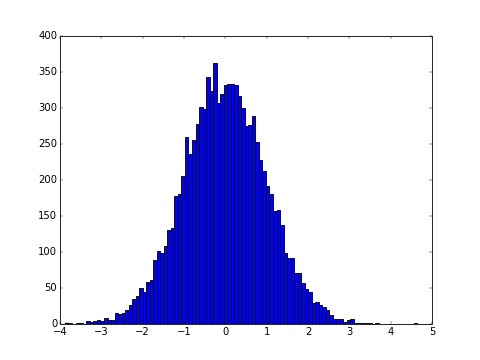
Wenn Sie sich nicht sicher sind, ob die gewünschten Zufallszahlen generiert werden, empfiehlt es sich, eine große Anzahl von Zufallszahlen zu generieren und ein Histogramm zu zeichnen. Hier wird ein Diagrammzeichnungsmodul namens matplotlib verwendet.
from numpy.random import *
import matplotlib.pyplot as plt
R = randn(10000) #Generieren Sie 10.000 Zufallszahlen mit Standardnormalverteilung
plt.hist(R, bins=100) #Erstellen Sie 100 Histogramme
plt.show() #Grafik anzeigen
Anwendung: Random Walk Generation
Generieren Sie eine zufällige Folge von rechts oder links, dh +1 oder -1, und nehmen Sie die kumulative Summe cumsum ().
from numpy import *
L = 1000 #Anzahl der Schritte
step = random.choice([-1,1],L) # +1 or -L 1 erzeugen
position = cumsum(step) #Positionswechsel

Recommended Posts