[PYTHON] Erzeugung hochdimensionaler Zufallszahlenvektoren ~ Latin Hypercube Sampling / Latin Super Square Sampling ~

Einführung

Eines der Probleme im hochdimensionalen Raum ist das Phänomen der sphärischen Konzentration. Das Phänomen der sphärischen Konzentration ist ein Phänomen, bei dem die Punktdichte auf der Oberfläche eines $ n $ -dimensionalen Superwürfels im hochdimensionalen Raum zunimmt. Dieses Phänomen verursacht das Problem, dass die Anzahl der Proben in der Nähe des Zentrums abnimmt, wenn im hochdimensionalen Raum gesucht oder die Monte-Carlo-Methode verwendet wird. In diesem Artikel möchte ich Latin Hypercube Sampling vorstellen, eine der Beispielmethoden zur Lösung dieses Problems. Es gibt auch eine bekannte Probenmethode unter Verwendung der Sobol-Säule.

Latin Hypercube Sampling-Algorithmus

Beim Abtasten von $ M $ -Punkten im $ n $ -Dimensionsraum unterteilt Latin Hypercube Sampling zuerst jede Achse in $ M $ -Gitter. In der folgenden Abbildung ist ein Beispiel angegeben, wenn $ n = 2 $ und $ M = 5 $.

Wählen Sie dann die Zellen einzeln aus, damit die Zeilen nicht jede Spalte abdecken.

In jeder ausgewählten Zelle werden Zufallszahlen generiert und als Stichprobenpunkte verwendet.

Dies verhindert die Auswahl von mehr als ein paar überlappenden Zellen, sodass der durchschnittliche Abstand zwischen einem Punkt und dem nächstgelegenen Punkt im Raum wahrscheinlich näher am Schwerpunkt von Zelle zu Zelle liegt (tatsächlich unterschiedlich, aber ein Bild). Mit anderen Worten, das Bild ist, dass es einfacher ist, den Raum mit weniger Proben gleichmäßiger zu sehen. Im obigen zweidimensionalen Beispiel beträgt die Gesamtzahl der Quadrate an den Kanten (Spalten A, E, 1 Zeile, 5 Zeilen) beispielsweise 16 und die Anzahl der internen Quadrate 9. Unter Berücksichtigung einer einfachen Wahrscheinlichkeit die Wahrscheinlichkeit, dass alle Proben draußen einfrieren

\frac{{}_{16} C _{5}}{{}_{25} C _{5}} = \frac{16 \times 15 \times 14 \times 13 \times 12}{25 \times 24 \times 23 \times 22 \times 21}=\frac{8 \times 13}{5 \times 23 \times 11} \simeq 8.2 \%

Es wird. Auf der anderen Seite werden bei Latin Hypercube Sampling immer Samples aus jeder Spalte abgetastet und es werden keine doppelten Zeilen zugelassen, sodass die Wahrscheinlichkeit, dass alle Samples außerhalb einfrieren, $ 0 % $ beträgt.

Übrigens, nach der vorliegenden manuellen Berechnung, wenn $ n = 3, M = 5 $, scheint es, dass alles draußen mit einer Wahrscheinlichkeit von $ 29 % $ für einheitliche Zufallszahlen und $ 25,9 % $ für Latin Hypercube Sampling verfestigt ist. Es scheint, dass es keinen großen Unterschied gibt, wenn die Anzahl der Abteilungen gering ist. (Ich werde später ein numerisches Experiment durchführen.)

Latin Hypercube Sampling Code

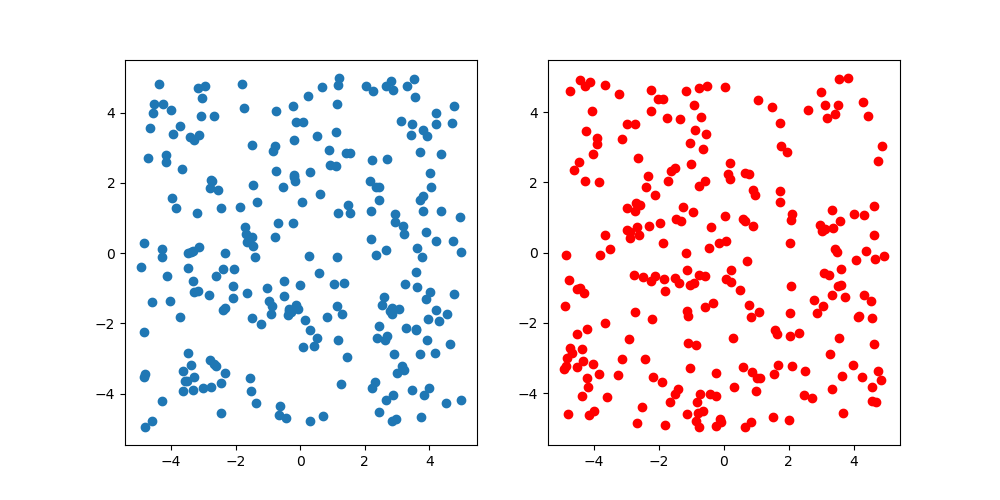
Vergleichen Sie für alle Fälle mit einer einheitlichen Zufallszahl. Die Anzahl der Stichproben beträgt 250, Blau ist eine einheitliche Zufallszahl und Rot ist Latin Hypercube Sampling. Wenn man die Figur betrachtet, sieht es nicht so aus, als gäbe es einen solchen Unterschied, aber es kann nicht geholfen werden, weil es zweidimensional ist. Da es schwierig ist, hohe Dimensionen zu visualisieren, ist dies das Ende dieser Überprüfung.

import numpy as np
import matplotlib.pyplot as plt 


n = 2
M = 250

lb, ub = -5., 5.

f = lambda x: (ub - lb) * x + lb
g = lambda x: (x - rng.uniform()) / M
rng = np.random.RandomState()
rs = f(rng.rand(M, n))

rnd_grid = np.array([rng.permutation(list(range(1, M + 1))) for _ in range(n)])
lhs = np.array([[f(g(rnd_grid[d][m])) for d in range(n)] for m in range(M)])


fig, ax = plt.subplots(1, 2, figsize=(10, 5)) 
ax[0].scatter(rs[:, 0], rs[:, 1]) 
ax[1].scatter(lhs[:, 0], lhs[:, 1], color="red")

plt.show()