[PYTHON] Multivariates LSTM mit Keras
Ich sehe oft univariate Zeitreihen in Keras, aber da bei der Vorhersage von Aktienkursen, Verkäufen usw. mehrere Faktoren eine Rolle spielen, habe ich diesmal versucht, anhand mehrerer Zeitreihendaten eine Vorhersage zu treffen. ..
Quelleneinführung
Code
Basierend auf dem in "MACHINE LEARNING MASTERY" eingeführten Code wird Multivariate unterstützt. Time Series Prediction with LSTM Recurrent Neural Networks in Python with Keras
Klicken Sie hier, um den vollständigen Code anzuzeigen, der auf jupyter angezeigt wird https://github.com/tizuo/keras/blob/master/LSTM%20with%20multi%20variables.ipynb
Daten
Beispieldaten werden aus dem Folgenden ausgeliehen. Sagen Sie den Eisverkauf ganz links voraus. Wie man Eis verkauft
| ice_sales | year | month | avg_temp | total_rain | humidity | num_day_over25deg |
|---|---|---|---|---|---|---|
| 331 | 2003 | 1 | 9.3 | 101 | 46 | 0 |
| 268 | 2003 | 2 | 9.9 | 53.5 | 52 | 0 |
| 365 | 2003 | 3 | 12.7 | 159.5 | 49 | 0 |
| 492 | 2003 | 4 | 19.2 | 121 | 61 | 3 |
| 632 | 2003 | 5 | 22.4 | 172.5 | 65 | 7 |
| 730 | 2003 | 6 | 26.6 | 85 | 69 | 21 |
| 821 | 2003 | 7 | 26 | 187.5 | 75 | 21 |
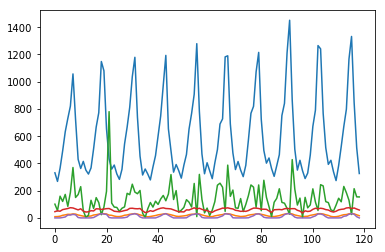
Datenstandardisierung
Standardisieren Sie die Daten. Es wurde erklärt, dass LSTM sensibel ist und die Nummern, die es verarbeitet, standardisiert werden müssen.
python
scaler = MinMaxScaler(feature_range=(0, 1))
dataset = scaler.fit_transform(dataset)
Separate Testdaten
Dieses Mal werden wir die Daten der zweiten Hälfte 1/3 vorhersagen, also werden wir sie von denen für das Lernen trennen.
python
train_size = int(len(dataset) * 0.67)
test_size = len(dataset) - train_size
train, test = dataset[0:train_size,:], dataset[train_size:len(dataset),:]
Datenformung
Da der Wert des nächsten Monats anhand des Werts bis vor 3 Monaten ermittelt wird, formatieren Sie ihn wie folgt. Erstellen Sie Variablen, die dies verwenden, und speichern Sie sie zu einem bestimmten Zeitpunkt in den Daten.
| Y | vor 3 Monaten | Vor 2 Monaten | Vor 1 Monat |
|---|---|---|---|
| Januar Wert | Oktoberwert | 1Januar Wert | Dezember Wert |
| Februar Wert | Novemberwert | 1Februar Wert | Januar Wert |
| März Wert | Dezember Wert | Januar Wert | Februar Wert |
Dieses Mal betrachten wir es als einen Satz pro Jahr, und Lookback erstellt Daten mit 12.
python
def create_dataset(dataset, look_back=1):
dataX, dataY = [], []
for i in range(len(dataset)-look_back-1):
xset = []
for j in range(dataset.shape[1]):
a = dataset[i:(i+look_back), j]
xset.append(a)
dataY.append(dataset[i + look_back, 0])
dataX.append(xset)
return numpy.array(dataX), numpy.array(dataY)
look_back = 12
trainX, trainY = create_dataset(train, look_back)
testX, testY = create_dataset(test, look_back)
Konvertieren Sie diese Daten in ein von keras LSTM akzeptiertes Format. [Anzahl der Zeilen]> [Anzahl der Variablen]> [Anzahl der Spalten (Anzahl der Suchvorgänge)]
python
trainX = numpy.reshape(trainX, (trainX.shape[0], trainX.shape[1], trainX.shape[2]))
testX = numpy.reshape(testX, (testX.shape[0], testX.shape[1], testX.shape[2]))
Modellieren
input_shape enthält die Anzahl der Variablen und die Anzahl der Suchvorgänge. Die Anzahl der Ausgänge wird wie im Beispiel gezeigt auf 4 eingestellt, ohne dies zu berücksichtigen.
python
model = Sequential()
model.add(LSTM(4, input_shape=(testX.shape[1], look_back)))
model.add(Dense(1))
model.compile(loss='mean_squared_error', optimizer='adam')
model.fit(trainX, trainY, epochs=1000, batch_size=1, verbose=2)
Überprüfung
Die Vorhersage ist die gleiche wie üblich.
python
trainPredict = model.predict(trainX)
testPredict = model.predict(testX)
Danach setzen Sie Y auf die nicht standardisierte Nummer zurück. Da der Skalierer nur akzeptiert wird, wenn er dieselbe Form wie der ursprüngliche Datensatz hat, wird der Wert für die Anzahl der vorhandenen Spalten mit 0 gefüllt. Bitte lassen Sie mich wissen, ob es einen intelligenteren Weg gibt.
python
pad_col = numpy.zeros(dataset.shape[1]-1)
def pad_array(val):
return numpy.array([numpy.insert(pad_col, 0, x) for x in val])
trainPredict = scaler.inverse_transform(pad_array(trainPredict))
trainY = scaler.inverse_transform(pad_array(trainY))
testPredict = scaler.inverse_transform(pad_array(testPredict))
testY = scaler.inverse_transform(pad_array(testY))
Schließlich wird die Standardabweichung angegeben.
python
trainScore = math.sqrt(mean_squared_error(trainY[:,0], trainPredict[:,0]))
print('Train Score: %.2f RMSE' % (trainScore))
testScore = math.sqrt(mean_squared_error(testY[:,0], testPredict[:,0]))
print('Test Score: %.2f RMSE' % (testScore))
Nach dem Ändern der Anzahl der Variablen wurde es wie folgt. Natürlich müssen Sie die zu werfende Variable auswählen.
| Ein Modell, das nur aus dem Verkauf von Eis gelernt wurde | Eis und 25 Grad oder mehr Tage | Alles | |
|---|---|---|---|
| Train Score | 30.20 RMSE | 15.19 RMSE | 8.44 RMSE |
| Test Score | 111.97 RMSE | 108.09 RMSE | 112.90 RMSE |

Recommended Posts