Einführung

Dies ist die dritte Ausgabe von PyTorch Official Tutorial nach Last time. Dieses Mal fahren wir mit [NEURAL NETWORKS] fort (https://pytorch.org/tutorials/beginner/blitz/neural_networks_tutorial.html).

Neuronale Netze

PyTorch baut mit dem Paket torch.nn ein neuronales Netzwerk auf. Die Modellkonstruktion wird durch Erben von nn.Module definiert. nn.Module implementiert eine Ebene und eine Vorwärtsmethode, die die Ausgabe zurückgibt.

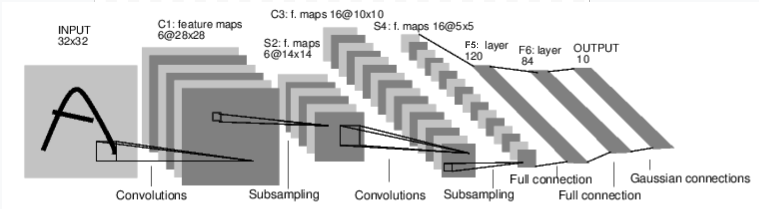
Das Bild oben (Fluss) ist ein Modell, das die Zahlen im Bild beurteilt. Es nimmt eine Eingabe (INPUT 32 x 32) entgegen, durchläuft mehrere Ebenen und gibt das Ergebnis aus (0 bis 9).

Die Abmessungen jeder Schicht ändern sich wie folgt. INPUT（32×32）⇒ C1（6×28×28）⇒ S2（6×14×14）⇒ C3（16×10×10）⇒ S4（6×5×5）⇒ F5（120）⇒ F6（84）⇒ OUTPUT（10）

Das Lernverfahren für das neuronale Netzwerk ist wie folgt.

Definieren Sie ein neuronales Netzwerk --Geben Sie den Datensatz ein
(Verarbeitung der Eingabe über das Netzwerk) --Berechnen Sie den Verlust
Reflektieren Sie den Gradienten in den Netzwerkparametern (Fehlerrückausbreitung)
Aktualisieren Sie die Netzwerkgewichte

Schauen wir uns jeden an.

Definieren Sie das Netzwerk

Wenn Sie das Netzwerk im obigen Bild definieren, ist dies der folgende Code.

import torch
import torch.nn as nn
import torch.nn.functional as F

class Net(nn.Module):

    def __init__(self):
        super(Net, self).__init__()
        # 1 input image channel, 6 output channels, 5x5 square convolution
        # kernel
        self.conv1 = nn.Conv2d(1, 6, 5)
        self.conv2 = nn.Conv2d(6, 16, 5)
        # an affine operation: y = Wx + b
        self.fc1 = nn.Linear(16 * 5 * 5, 120)
        self.fc2 = nn.Linear(120, 84)
        self.fc3 = nn.Linear(84, 10)

    def forward(self, x):
        # Max pooling over a (2, 2) window
        x = F.max_pool2d(F.relu(self.conv1(x)), (2, 2))
        # If the size is a square you can only specify a single number
        x = F.max_pool2d(F.relu(self.conv2(x)), 2)
        x = x.view(-1, self.num_flat_features(x))
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = self.fc3(x)
        return x

    def num_flat_features(self, x):
        size = x.size()[1:]  # all dimensions except the batch dimension
        num_features = 1
        for s in size:
            num_features *= s
        return num_features

net = Net()
print(net)

Net(
  (conv1): Conv2d(1, 6, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
  (fc1): Linear(in_features=400, out_features=120, bias=True)
  (fc2): Linear(in_features=120, out_features=84, bias=True)
  (fc3): Linear(in_features=84, out_features=10, bias=True)
)

Definieren Sie jede Ebene mit init. torch.nn.Module wiederholt die Berechnung ausgehend von der Eingabeebene, berechnet die Koeffizienten und Gewichte und leitet sie an die nächste Ebene weiter. Dies wird als Vorwärtsausbreitung bezeichnet. torch.nn.Module ist ein "Forward Propagation Neural Network". Schreiben Sie diese Vorwärtsausbreitungsberechnung in die Vorwärtsmethode. Der obige Code repräsentiert den Inhalt des Bildes im Code. Das Berechnungsergebnis der Vorwärtsausbreitung kann dann mit der Module.parameters () -Methode erhalten werden.

params = list(net.parameters())
print(len(params))
print(params[0].size())  # conv1's .weight

10
torch.Size([6, 1, 5, 5])

Geben Sie den Datensatz ein

[[Autograd: Auto Differentiation](https://pytorch.org/tutorials/beginner/blitz/autograd_tutorial.html#sphx-glr-beginner] von Last time Wie wir in -blitz-autograd-tutorial-py) gesehen haben, können neuronale Netze auch Gradienten berechnen. Der Gradient wird berechnet, indem der Eingang (32x32) eingegeben wird, der für das wie folgt definierte neuronale Netzwerk geeignet ist. (Obwohl es sich ein wenig vom Beispielcode unterscheidet, wird "require_grad = True" hinzugefügt, damit der Gradient berechnet werden kann.)

input = torch.randn(1, 1, 32, 32, requires_grad=True)
out = net(input)
print(out)

tensor([[-0.0769,  0.1520, -0.0556,  0.0384, -0.0847,  0.1081, -0.0190, -0.0522,
         -0.0523, -0.0007]], grad_fn=<AddmmBackward>)

net.zero_grad()
out.backward(torch.randn(1, 10))

Im Folgenden können Sie das Ergebnis der Rückausbreitung (Rückausbreitung) ausgeben.

print(input.grad)

Verlust berechnen

Die Verlustfunktion vergleicht den vom Netzwerk ausgegebenen Wert mit den Lehrerdaten und bewertet, wie weit das Trainingsergebnis von den Lehrerdaten entfernt ist. Das nn-Paket enthält mehrere Verlustfunktionen (https://pytorch.org/docs/stable/nn.html#loss-functions). Eine grundlegende Verlustfunktion ist nn.MSELoss. MSELoss wird als mittlerer quadratischer Fehler bezeichnet, der die Differenz zwischen dem Trainingsergebnis und den Lehrerdaten quadriert und den Durchschnitt berechnet.

output = net(input)
target = torch.randn(10)  # a dummy target, for example
target = target.view(1, -1)  # make it the same shape as output
criterion = nn.MSELoss()

loss = criterion(output, target)
print(loss)

Das Trainingsergebnis des neuronalen Netzwerks wird in der Ausgabe gehalten. Stellen Sie die Lehrerdaten im Ziel ein. (Diesmal ist es ein zufälliger Wert) Stellen Sie die Verlustfunktion auf MSELoss ein. Der Fehler zwischen dem Trainingsergebnis und den Lehrerdaten wird für den Verlust berechnet.

tensor(1.1126, grad_fn=<MseLossBackward>)

Fehler bei der Weitergabe

Der Zweck des Lernens eines neuronalen Netzwerks besteht darin, Fehler zu minimieren. Es gibt verschiedene Algorithmen (Optimierungsalgorithmen) zur Minimierung. Gemeinsam ist ihnen jedoch, dass der Gradient berechnet werden muss. Der Gradient kann durch das Fehlerrückausbreitungsverfahren berechnet werden. Mit Pytorch können Sie den Gradienten einfach berechnen, indem Sie loss.backward () ausführen. Sie können den Gradienten von conv1 vor und nach dem Aufruf von loss.backward () im folgenden Code sehen.

net.zero_grad()     #Nullgradient für alle Parameter (Initialisierung)

print('conv1.bias.grad before backward')
print(net.conv1.bias.grad)

loss.backward()

print('conv1.bias.grad after backward')
print(net.conv1.bias.grad)

conv1.bias.grad before backward
tensor([0., 0., 0., 0., 0., 0.])
conv1.bias.grad after backward
tensor([-0.0033,  0.0033,  0.0027,  0.0030,  0.0031, -0.0053])

Aktualisieren Sie die Netzwerkgewichte

Wie bereits erwähnt, werden beim Lernen die Parameter angepasst, um den Fehler zu minimieren (Verlustfunktion). Der grundlegendste Algorithmus (Optimierungsalgorithmus) dafür ist der "stochastische Gradientenabstieg (SGD)". Dieses Tutorial befasst sich nicht mit den Details des probabilistischen Gradientenabfalls (SGD), kann jedoch mit einfachem Code implementiert werden.

import torch.optim as optim

# create your optimizer
optimizer = optim.SGD(net.parameters(), lr=0.01)

# in your training loop:
optimizer.zero_grad()   # zero the gradient buffers
output = net(input)
loss = criterion(output, target)
loss.backward()
optimizer.step()    # Does the update

Neben der probabilistischen Gradientenabstiegsmethode (SGD) gibt es verschiedene Optimierungsalgorithmen wie Nesterov-SGD, Adam und RMSProp. torch.optim Das Paket enthält verschiedene Optimierungsalgorithmen (Optimierer).

Schließlich

Das ist alles für PyTorchs drittes Tutorial, Neuronale Netze. Ich habe das Gefühl, ein wenig über das grundlegende neuronale Netzwerk zu verstehen.

Nächstes Mal möchte mit dem vierten Tutorial "TRAINING A CLASSIFIER" fortfahren.

Geschichte

2020/04/22 Erste Ausgabe veröffentlicht 29.04.2020 Nächster Link hinzugefügt

[PYTHON] [PyTorch Tutorial ③] NEURALE NETZWERKE