Python: Diagramm der zweidimensionalen Datenverteilung (Schätzung der Kerneldichte)
Einführung
Ich wollte den Verteilungsstatus der Daten in zwei Dimensionen verteilt sehen, also habe ich versucht, die Kerneldichte mit `scipy.stats.gaussian_kde``` zu schätzen. Das Ergebnisdiagramm ist wie folgt. ( `bw_method = 'scott'```)

Übrigens wird die einfache Regressionsanalyse reibungslos mit `` `numpy``` wie folgt durchgeführt. (Wenn Sie verschiedene Dinge tun, ist es wichtig, dass dieser Code sofort herauskommt und verwendet werden kann, daher wage ich es, ihn aufzuschreiben.)
def sreq(x,y):
# y=a*x+b
res=np.polyfit(x, y, 1)
a=res[0]
b=res[1]
coef = np.corrcoef(x, y)
r=coef[0,1]
return a,b,r
Wie macht man
Das Verfahren war wie folgt. Danke, Plakat.
Der Einfallsreichtum ist wie folgt.
Da die + -Anzeige auf der logarithmischen Achse einfacher ist, habe ich die logarithmische Achse gewählt, wollte aber auch die numerischen Werte auf der Achse lesen, also habe ich die logarithmische Achse manuell gezeichnet. Die Datenverarbeitung erfolgt unter Verwendung des gemeinsamen Logarithmus der Rohdaten.
- Ich habe das Intervall für das Zeichnen von Konturlinien selbst gesteuert. Da die Wahrscheinlichkeitsdichte mit
`gaussian_kde``` erhalten werden kann, setzen Sie den oberen Rand dieses Wertes auf 1 und zeichnen Sie eine Linie bei`[0.01, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0] `` `. Es gibt. Der Mindestwert von 0,01 in der Liste wurde visuell festgelegt, um den Bereich der Daten abzudecken. Der Maximalwert von 1,0 wird hinzugefügt, da ohne ihn der Bereich von 0,9 oder mehr nicht gefärbt und umrissen wird. Beachten Sie, dass ** dieser Wert keinen Wahrscheinlichkeitswert ** angibt. Es dient nur zum Anpassen des Erscheinungsbilds.
Versuchen Sie, die Parameter zu ändern. .. ..
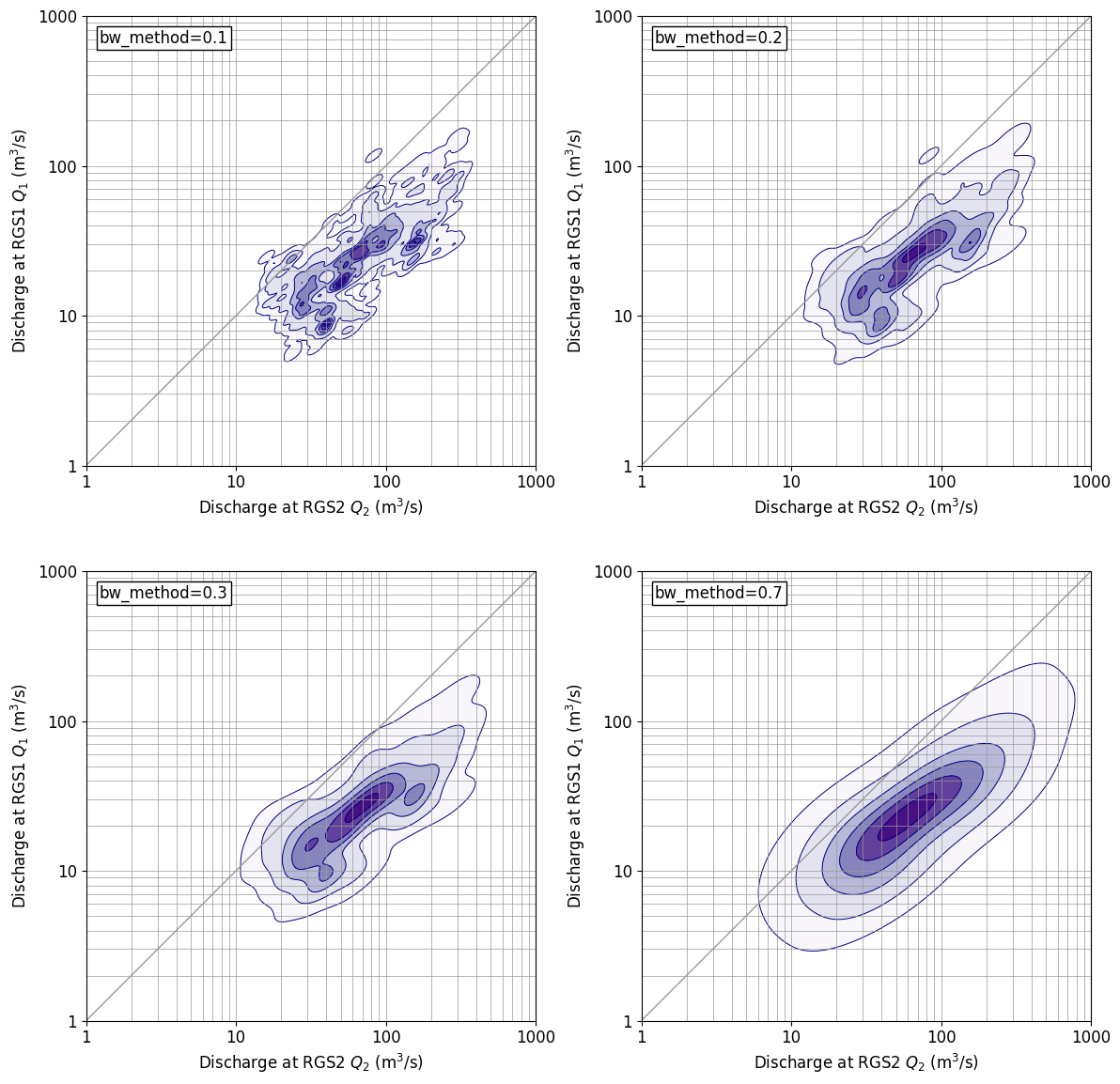
gaussin_bw für kde_Es gibt einen Parameter namens method. Wenn Sie diesen ändern, können Sie die Feinheit der Anzeige der Verteilungsform ändern. Das oben gezeigte Ergebnisdiagramm ist die Standardeinstellung bw_method=Im Fall von "Scott", bw unten_Die Abbildung beim Ändern der Methode wird angezeigt. bw_method=0.Wenn es 3 ist, ist die Verteilung nahe am Standard. bw_Wenn der Wert der Methode zunimmt, wird die Anzeige gröber und bw_method=0.Wenn es 7 ist, liegt die Anzeige nahe an der normalen zweidimensionalen Normalverteilung.
## Programm
Das Programm, das das in "Einführung" gezeigte Ergebnisdiagramm erstellt hat, ist unten dargestellt. Wenn Sie dieses Programm ausprobieren möchten, versuchen Sie bitte, die Daten nach Ihren Wünschen zu erstellen.
```python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.stats import gaussian_kde
def sreq(x,y):
# y=a*x+b
res=np.polyfit(x, y, 1)
a=res[0]
b=res[1]
coef = np.corrcoef(x, y)
r=coef[0,1]
return a,b,r
def inp_obs():
fnameR='df_rgs1_tank_inp.csv'
df1_obs=pd.read_csv(fnameR, header=0, index_col=0) # read excel data
df1_obs.index = pd.to_datetime(df1_obs.index, format='%Y/%m/%d')
df1_obs=df1_obs['2016/01/01':'2018/12/31']
#
fnameR='df_rgs2_tank_inp.csv'
df2_obs=pd.read_csv(fnameR, header=0, index_col=0) # read excel data
df2_obs.index = pd.to_datetime(df2_obs.index, format='%Y/%m/%d')
df2_obs=df2_obs['2016/01/01':'2018/12/31']
#
return df1_obs,df2_obs
def drawfig(x,y,sstr,fnameF):
fsz=12
xmin=0; xmax=3
ymin=0; ymax=3
plt.figure(figsize=(12,6),facecolor='w')
plt.rcParams['font.size']=fsz
plt.rcParams['font.family']='sans-serif'
#
for iii in [1,2]:
nplt=120+iii
plt.subplot(nplt)
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.xlabel('Discharge at RGS2 $Q_2$ (m$^3$/s)')
plt.ylabel('Discharge at RGS1 $Q_1$ (m$^3$/s)')
plt.gca().set_aspect('equal',adjustable='box')
plt.xticks([0,1,2,3], [1,10,100,1000])
plt.yticks([0,1,2,3], [1,10,100,1000])
bb=np.array([1,2,3,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90,100,200,300,400,500,600,700,800,900,1000])
bl=np.log10(bb)
for a0 in bl:
plt.plot([xmin,xmax],[a0,a0],'-',color='#999999',lw=0.5)
plt.plot([a0,a0],[ymin,ymax],'-',color='#999999',lw=0.5)
plt.plot([xmin,xmax],[ymin,ymax],'-',color='#999999',lw=1)
#
if iii==1:
plt.plot(x,y,'o',ms=2,color='#000080',markerfacecolor='#ffffff',markeredgewidth=0.5)
a,b,r=sreq(x,y)
x1=np.min(x)-0.1; y1=a*x1+b
x2=np.max(x)+0.1; y2=a*x2+b
plt.plot([x1,x2],[y1,y2],'-',color='#ff0000',lw=2)
tstr=sstr+'\n$\log(Q_1)=a * \log(Q_2) + b$'
tstr=tstr+'\na={0:.3f}, b={1:.3f} (r={2:.3f})'.format(a,b,r)
#
if iii==2:
tstr=sstr+'\n(kernel density estimation)'
xx,yy = np.mgrid[xmin:xmax:0.01,ymin:ymax:0.01]
positions = np.vstack([xx.ravel(),yy.ravel()])
value = np.vstack([x,y])
kernel = gaussian_kde(value, bw_method='scott')
#kernel = gaussian_kde(value, bw_method=0.1)
f = np.reshape(kernel(positions).T, xx.shape)
f=f/np.max(f)
ll=[0.01, 0.1, 0.3, 0.5, 0.7, 0.9, 1.0]
plt.contourf(xx,yy,f,cmap=cm.Purples,levels=ll)
plt.contour(xx,yy,f,colors='#000080',linewidths=0.7,levels=ll)
xs=xmin+0.03*(xmax-xmin)
ys=ymin+0.97*(ymax-ymin)
plt.text(xs, ys, tstr, ha='left', va='top', rotation=0, size=fsz,
bbox=dict(boxstyle='square,pad=0.2', fc='#ffffff', ec='#000000', lw=1))
#
plt.tight_layout()
plt.savefig(fnameF, dpi=100, bbox_inches="tight", pad_inches=0.1)
plt.show()
def main():
df1_obs, df2_obs =inp_obs()
fnameF='_fig_cor_test1.png'
sstr='Observed discharge (2016-2018)'
xx=df2_obs['Q'].values
yy=df1_obs['Q'].values
xx=np.log10(xx)
yy=np.log10(yy)
drawfig(xx,yy,sstr,fnameF)
#==============
# Execution
#==============
if __name__ == '__main__': main()
das ist alles
Recommended Posts