3. Verarbeitung natürlicher Sprache durch Python 3-1. Wichtiges Tool zur Wortextraktion TF-IDF-Analyse [Originaldefinition]
- Bei der Verarbeitung natürlicher Sprache besteht eines der spezifischen Ziele darin, "wichtige Wörter zu extrahieren, die einen bestimmten Satz charakterisieren".
- Wenn Sie Wörter extrahieren, nehmen Sie zuerst die Wörter auf, die im Text am häufigsten vorkommen. Am Anfang der Liste stehen in der Reihenfolge der Häufigkeit des Auftretens nur die Wörter, die üblicherweise in allen Sätzen verwendet werden.
- Selbst wenn Sie sich auf die Nomenklatur mit Teilwortinformationen beschränken, werden viele Allzweckwörter, die keine bestimmte Bedeutung haben, wie "Ding" und "Zeit", oben angezeigt. Schließen Sie sie daher als Stoppwörter aus. Verarbeitung wie erforderlich.
⑴ Die Idee von TF-IDF
- ** TF-IDF (Termfrequenz - Inverse Dokumentfrequenz) **, wörtlich übersetzt als "Termfrequenz - Inverse Dokumentfrequenz".
- ** Die Vorstellung, dass ein Wort, das häufig vorkommt, aber die Anzahl der Dokumente, in denen das Wort vorkommt, gering ist **, dh ein Wort, das nicht überall vorkommt, wird als ** charakteristisches und wichtiges Wort ** beurteilt. ist.
- Die meisten von ihnen sind für Wörter, aber sie können auch auf Buchstaben und Phrasen angewendet werden, und die Einheiten von Dokumenten können auch auf verschiedene Arten angewendet werden.
⑵ Definition des TF-IDF-Wertes
** Häufigkeit des Auftretens $ tf $ multipliziert mit dem Seltenheitsindex $ idf $ **
tfidf=tf×idf - $ tf_ {ij} $ (Häufigkeit des Auftretens des Wortes $ i $ im Dokument $ j $) × $ idf_ {i} $ ($ log $, die Umkehrung der Anzahl der Dokumente, die das Wort $ i $ enthalten)
** Die Häufigkeit des Auftretens $ tf $ und der Koeffizient $ idf $ sind wie folgt definiert **
- $ tf_ {ij} = \ dfrac {n_ {ij}} {\ sum_ {k} n_ {kj}} = \ dfrac {Anzahl der Vorkommen von Wort i in Dokument j} {Anzahl der Vorkommen aller Wörter in Dokument j Summe} $
idf_{i}=\log \dfrac{|D|}{|\{d:d∋t_{i}\}|} = \log{\dfrac{Anzahl aller Dokumente}{Anzahl der Dokumente, die das Wort i enthalten}}
(3) Berechnungsmechanismus nach der ursprünglichen Definition
#Import der numerischen Berechnungsbibliothek
from math import log
import pandas as pd
import numpy as np
➀ Bereiten Sie eine Wortdatenliste vor
- Berechnen Sie $ tfidf $ der drei Zielwörter unter der Annahme, dass die folgende Wortliste für die sechs Dokumente nach der Vorverarbeitung wie der morphologischen Analyse erstellt wurde.
docs = [
["Wort 1", "Wort 3", "Wort 1", "Wort 3", "Wort 1"],
["Wort 1", "Wort 1"],
["Wort 1", "Wort 1", "Wort 1"],
["Wort 1", "Wort 1", "Wort 1", "Wort 1"],
["Wort 1", "Wort 1", "Wort 2", "Wort 2", "Wort 1"],
["Wort 1", "Wort 3", "Wort 1", "Wort 1"]
]
N = len(docs)
words = list(set(w for doc in docs for w in doc))
words.sort()
print("Anzahl der Dokumente:", N)
print("Zielwörter:", words)

➁ Definieren Sie eine Berechnungsfunktion
- Definieren Sie eine Funktion, die die Häufigkeit des Auftretens $ tf $, den Koeffizienten $ idf $ und $ tfidf $ multipliziert mit ihnen im Voraus berechnet.
#Definition der Funktion tf
def tf(t, d):
return d.count(t)/len(d)
#Definition der Funktion idf
def idf(t):
df = 0
for doc in docs:
df += t in doc
return np.log10(N/df)
#Definition der Funktion tfidf
def tfidf(t, d):
return tf(t,d) * idf(t)
➂ Beachten Sie das Berechnungsergebnis von TF
- Schauen wir uns als Referenz Schritt für Schritt die Berechnungsergebnisse von $ tf $ und $ idf $ an.
#Berechne tf
result = []
for i in range(N):
temp = []
d = docs[i]
for j in range(len(words)):
t = words[j]
temp.append(tf(t,d))
result.append(temp)
pd.DataFrame(result, columns=words)
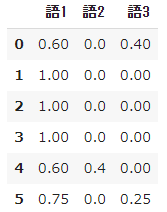
➃ Beachten Sie die IDF-Berechnungsergebnisse
#IDf berechnen
result = []
for j in range(len(words)):
t = words[j]
result.append(idf(t))
pd.DataFrame(result, index=words, columns=["IDF"])
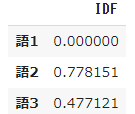
- Der Koeffizient $ idf $ für Wort 1, der in allen sechs Dokumenten vorkommt, ist 0, und Wort 2, das nur in einem Dokument vorkommt, hat den größten Wert von 0,778151.
➄ TF-IDF-Berechnung
#Berechnen Sie tfidf
result = []
for i in range(N):
temp = []
d = docs[i]
for j in range(len(words)):
t = words[j]
temp.append(tfidf(t,d))
result.append(temp)
pd.DataFrame(result, columns=words)
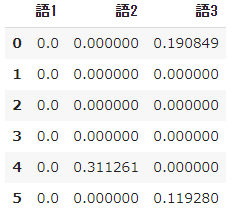
- $ Tfidf $ in Wort 1 hat einen Koeffizienten $ idf $ von 0, egal wie oft es erscheint, es wird 0 sein.
- Außerdem ist TF-IDF ein Index, der ursprünglich zum Abrufen von Informationen vorgeschlagen wurde. Bei Wörtern, die nicht einmal vorkommen, wird der Nenner bei der Berechnung von $ idf $ zu 0 (sogenannte Nullteilung), und es tritt ein Fehler auf. Es wird sein.
⑷ Berechnung durch Scikit-Learn
- Als Reaktion auf diese Probleme wird die TF-IDF-Bibliothek
tfidfVectorizervon scikit-learn mit einer etwas anderen Definition als der ursprünglichen Definition implementiert.
# scikit-lerne TF-IDF-Bibliothek importieren
from sklearn.feature_extraction.text import TfidfVectorizer
- Berechnen wir $ tfidf $ mit
TfidfVectorizerfür die Wortdatenliste der oben genannten 6 Dokumente.
#Eindimensionale Liste
docs = [
"Wort 1 Wort 3 Wort 1 Wort 3 Wort 1",
"Wort 1 Wort 1",
"Wort 1 Wort 1 Wort 1",
"Wort 1 Wort 1 Wort 1 Wort 1",
"Wort 1 Wort 1 Wort 2 Wort 2 Wort 1",
"Wort 1 Wort 3 Wort 1 Wort 1"
]
#Modell generieren
vectorizer = TfidfVectorizer(smooth_idf=False)
X = vectorizer.fit_transform(docs)
#In einem Datenrahmen dargestellt
values = X.toarray()
feature_names = vectorizer.get_feature_names()
pd.DataFrame(values,
columns = feature_names)
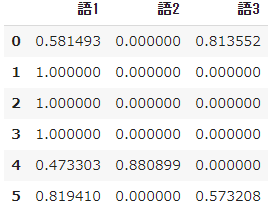
- $ Tfidf $ für Wort 1 ist nicht mehr in jedem Dokument 0 und unterscheidet sich von der ursprünglichen Definition für Wort 2 und 3 mit Ausnahme von Dokumenten, die ursprünglich 0 waren.
- Lassen Sie uns also das Ergebnis von Scikit-Learn basierend auf der ursprünglichen Definition reproduzieren.
⑸ Reproduzieren Sie das Ergebnis von Scikit-Learn
➀ IDF-Formel geändert
#Definition der Funktion idf
def idf(t):
df = 0
for doc in docs:
df += t in doc
#return np.log10(N/df)
return np.log(N/df)+1
- Ändern Sie "np.log10 (N / df)" in "np.log (N / df) + 1"
- Mit anderen Worten, ändern Sie den regulären Logarithmus mit der Basis 10 in den natürlichen Logarithmus mit der Basisnummer e und addieren Sie +1.
#IDf berechnen
result = []
for j in range(len(words)):
t = words[j]
result.append(idf(t))
pd.DataFrame(result, index=words, columns=["IDF"])
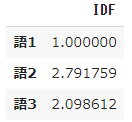
➁ Beachten Sie das Berechnungsergebnis von TF-IDF
#Berechnen Sie tfidf
result = []
for i in range(N):
temp = []
d = docs[i]
for j in range(len(words)):
t = words[j]
temp.append(tfidf(t,d))
result.append(temp)
pd.DataFrame(result, columns=words)
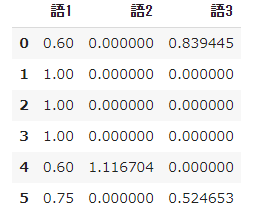
➂ L2-Regularisierung der TF-IDF-Berechnungsergebnisse
- Schließlich ** regelt ** L2 ** das Berechnungsergebnis von $ tfidf $.
- Skalieren Sie die Werte und konvertieren Sie sie so, dass sie alle quadriert und zu 1 summiert werden.
- Der Grund, warum eine Regularisierung erforderlich ist, besteht darin, zu zählen, wie oft jedes Wort in jedem Dokument vorkommt. Da jedoch jedes Dokument eine andere Länge hat, sind die Wörter umso länger, je länger das Dokument ist.
- Durch Entfernen des Effekts der Gesamtzahl solcher Wörter ist es möglich, die Häufigkeit des Auftretens von Wörtern relativ zu vergleichen.
#Berechnen Sie den Normwert gemäß der Definition nur in Dokument 1 als Versuch
x = np.array([0.60, 0.000000, 0.839445])
x_norm = sum(x**2)**0.5
x_norm = x/x_norm
print(x_norm)
#Quadrieren Sie sie und addieren Sie sie, um sicherzustellen, dass sie 1 sind
np.sum(x_norm**2)

- Lass uns hier mit Scikit-Learn genießen.
# scikit-Importieren Sie die Regularisierungsbibliothek
from sklearn.preprocessing import normalize
#L2-Regularisierung
result_norm = normalize(result, norm='l2')
#In einem Datenrahmen dargestellt
pd.DataFrame(result_norm, columns=words)
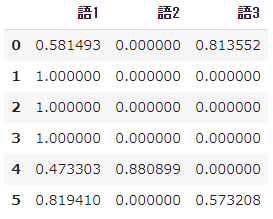
- Zusammenfassend lässt sich sagen, dass die TF-IDF von scikit-learn die beiden Nachteile der ursprünglichen Definition löst.
- Vermeiden Sie Null, indem Sie den natürlichen Logarithmus in der Formel für den Koeffizienten $ idf $ verwenden und +1 addieren. Die Umwandlung vom gemeinsamen Logarithmus in den natürlichen Logarithmus beträgt übrigens etwa das 2,303-fache.
- Darüber hinaus eliminiert die L2-Regularisierung den Effekt des Unterschieds in der Anzahl der Wörter aufgrund der Länge jedes Dokuments.
- Das Prinzip von TF-IDF ist sehr einfach, aber Scikit-Learn hat verschiedene Parameter, und es scheint je nach Aufgabe Raum für Einstellungen zu geben.
Recommended Posts