Ich habe mir kürzlich das Video und die Folien einer Klasse mit dem Titel "Deep Learning for Natural Language Processing" an der Stanford University angesehen, aber ich habe es gerade gesehen. Ich habe beschlossen, das Vorlesungsprotokoll zu veröffentlichen, während ich den Inhalt zusammenfasse, da es anscheinend nicht in meinem Körper verbleibt.

Diesmal ist es die zweite "Simple Word Vector-Darstellung: word2vec, GloVe". Das erste Mal war ein Intro, also habe ich es übersprungen.

Wie man die Bedeutung für jedes Wort und seine Probleme ausdrückt

Wenn Ihr Computer die Bedeutung eines Wortes erkennen soll, können Sie eine handgefertigte Klassifizierungstabelle wie WordNet verwenden. Es gibt jedoch ein Problem mit solchen Ausdrücken.

-Es drückt keine feinen Nuancen aus (Unterschiede in Synonymen wie geschickt, kompetent, gut, geübt, kompetent, geschickt)

Ich kann nicht mit neuen Wörtern umgehen
Subjektiv
Der Mensch muss sein Bestes geben
Schwierig, genaue Wortähnlichkeit zu berechnen

Deshalb funktioniert es nicht sehr gut, die Bedeutung jedes Wortes auszudrücken.

Fokus auf Verteilungsähnlichkeit: Matrix für das gleichzeitige Auftreten von Wörtern

Die Ähnlichkeit von Wörtern kann durch die Verteilung der Wörter berücksichtigt werden, die im Dokumentensatz vorkommen, nicht durch die sprachliche Bedeutung der Wörter. Dies ist eine der erfolgreichsten Ideen im modernen statistischen NLP.

Zum Beispiel, wenn Sie zwei Sätze haben, in denen das Wort "Banking" erscheint

Ich denke, dass das in Orange gemalte Wort "Banking" bedeutet.

Um dieses Modell auf einem Computer funktionsfähig zu machen, sollte das gleichzeitige Auftreten von Wörtern durch eine Matrix dargestellt werden. Es besteht die Möglichkeit, die Größe des orangefarbenen Teils für das gesamte Dokument oder bis zu N Zeichen davor und danach festzulegen (dieser Bereich wird als Fenster bezeichnet). Durch die Bereitstellung eines Fensters kann das Wort im Dokument enthalten sein Man kann sagen, dass die Position und Bedeutung des Aussehens berücksichtigt werden kann. Die Größe des Fensters beträgt in der Regel 5 bis 10. Sie können das Gewicht links und rechts vom Wort ändern und das Wort entsprechend seiner Entfernung gewichten.

Beispiel einer Matrix für das gleichzeitige Auftreten von Wörtern

I like deep learning.
I like NLP.
I enjoy flying.

Die Koexistenzmatrix lautet wie folgt, wenn das Dokument ein Korpus ist, die Fenstergröße 1 beträgt und die Gewichte links und rechts vom Wort gleich sind.

Probleme mit der Matrix für das gleichzeitige Auftreten von Wörtern

――Da die Anzahl der Dimensionen entsprechend den angezeigten Wörtern zunimmt, wird die Matrix umso größer und spärlicher, je größer der Korpus ist. ――Wenn die Anzahl der Dimensionen zunimmt, ist möglicherweise eine große Menge an Speicherkapazität erforderlich, sofern dies nicht vorgesehen ist.

Kurz gesagt, es fehlt die Robustheit.

Die Grundidee für diese Probleme besteht darin, sie kleiner und dichter zu machen, indem nur die wichtigen Informationen extrahiert werden, anstatt alles in einer Reihe aufzustellen. Im Allgemeinen möchte ich es auf etwa 25 bis 1000 Dimensionen komprimieren. Wie machst du das?

Machen Sie das Wort Co-Auftrittsmatrix dicht

Es wurden mehrere Methoden vorgeschlagen. Hier werden SVD, word2vec und GloVe aufgenommen.

SVD

Die erste Methode besteht darin, eine Singularitätszerlegung (SVD) der Matrix durchzuführen. SVD ist in numpy implementiert, sodass Sie es ausprobieren können.

import numpy as np

la = np.linalg
words = ["I", "like", "enjoy", "deep",
         "learning", "NLP", "flying", "."]

#↑ Manuelle Matrix für das gleichzeitige Auftreten von Wörtern
X = np.array([
    [0,2,1,0,0,0,0,0],
    [2,0,0,1,0,1,0,0],
    [1,0,0,0,0,0,1,0],
    [0,1,0,0,1,0,0,0],
    [0,0,0,1,0,0,0,1],
    [0,1,0,0,0,0,0,1],
    [0,0,1,0,0,0,0,1],
    [0,0,0,0,1,1,1,0]
])

# SVD
U, s, Vh = la.svd(X, full_matrices=False)

Dies macht den ursprünglich spärlichen Wort-Koexistenzvektor dichter. Zum Beispiel für das Wort "tief"

>>> print(X[3])
[0 1 0 0 1 0 0 0]

Es war

>>> print(U[3])
[ -2.56274005e-01   2.74017533e-01   1.59810848e-01  -2.77555756e-16
  -5.78984617e-01   6.36550929e-01   8.88178420e-16  -3.05414877e-01]

werden. Es fühlt sich wie etwas allein an, aber wenn ich nur die 0. und 1. Dimension nehme und jedes Wort in einem 2D-Raum zeichne, sind "tief" und "NLP" irgendwie nah oder "genießen" Es scheint, dass "und" Lernen "einander ähnlich sind.

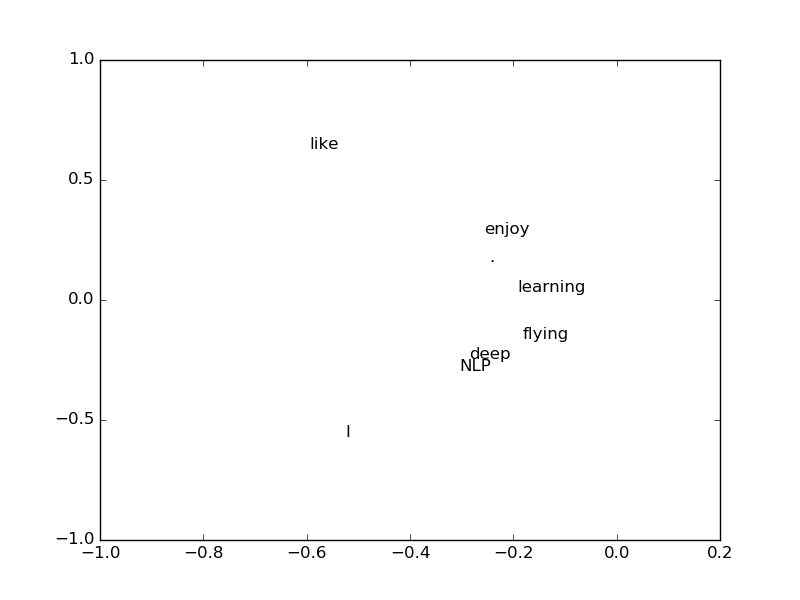
Inhalt der SVD

Ich bin übrigens der Meinung, dass die Gültigkeit der Verwendung von SVD in der Vorlesung nicht erwähnt wurde. Da ich "Latent Semantic Analysis" erwähnt habe, kann es sein, dass Sie dort suchen sollten.

Unter Verwendung von SVD ist die $ n \ times n $ -Matrix $ X $ von Rang $ r $ die orthogonale Spaltenmatrix $ U $ und $ V $ von $ n \ times r $ und das diagonale Element von $ D $. Sie kann wie folgt zerlegt werden, indem die Matrix $ r \ times r $ $ S $ verwendet wird, in der einzelne Werte angeordnet sind.

X = U S V^T

Zu diesem Zeitpunkt, wenn Sie $ S V ^ T $ als $ W $ setzen

X = U W

werden. Man kann sagen, dass $ X $ eine Art Matrix $ W $ ist, die von $ U $ konvertiert wird. Da $ U $ eine spaltenorthogonale Matrix ist, sind die Spaltenvektoren übrigens unabhängig voneinander. Mit anderen Worten, es ist die Basis eines Raums, aber in Wirklichkeit ist es ein Wortraum, und jeder Spaltenvektor kann als eine mögliche Bedeutung angesehen werden.

Probleme mit SVD

SVD kann auch verallgemeinert und auf $ n \ times m $ Matrizen angewendet werden. Wenn $ n <m $ ist, betragen die Berechnungskosten für die Berechnung aus einer solchen Matrix $ O (mn ^ 2) $, sodass die große Größe nicht auf die Matrix angewendet werden kann. Deshalb ist es schwierig, neue Wörter aufzunehmen, wenn sie herauskommen.

word2vec

Es wurden verschiedene Methoden vorgeschlagen, aber das von Mikolov et al. Aus dem Jahr 2013 vorgeschlagene word2vec zieht die Aufmerksamkeit auf sich.

Die Idee von word2vec besteht darin, "Wörter, die in der Umgebung vorkommen, wahrscheinlich zu behandeln, anstatt sich direkt mit der Anzahl der gleichzeitigen Vorkommen zu befassen". Es ist schneller und einfacher, neue Wörter hinzuzufügen.

word2vec ist auch C-Sprache, Java, [Python](http: // radimrehurek). Es gibt eine Implementierung in com / gensim /), damit Sie es versuchen können.

Theorie

Betrachten Sie ein Fenster der Größe c vor und nach jedem Wort, die Wahrscheinlichkeit, dass es dort für jedes Wort im Fenster erscheint, und verwenden Sie die Summe davon als Zielfunktion, um die wahrscheinlichste zu schätzen. Das Protokoll wird erstellt, um die spätere Berechnung zu vereinfachen.

J(\theta) = \frac{1}{T} \sum_{t=1}^T \sum_{-c \leq j \leq c,j \neq 0} \log p(w_{t+j} | w_t)

Vektorbeziehung

Wörter werden mit word2vec als Vektoren dargestellt. Zu diesem Zeitpunkt ist bekannt, dass aus der Differenz zwischen Wortvektoren ein interessantes Ergebnis erhalten werden kann.

Wenn Sie beispielsweise den Mann vom König subtrahieren und die Frau hinzufügen, kommt dies dem Vektor der Königin sehr nahe. Es kann angenommen werden, dass der Vektor, der durch Subtrahieren des Menschen vom König gebildet wird, ein mächtiges Konzept darstellt.

X_{king} - X_{man} + X_{woman} \approx X_{queen}

Es scheint eine Geschichte zu geben, dass, wenn Sie den japanischen Korpus mit Mecab analysieren und dasselbe tun, Sie Yahoo von Google ziehen und Toyota hinzufügen, um Nissan zu werden.

https://plus.google.com/107334123935896432800/posts/JvXrjzmLVW4

Geschwindigkeit

word2vec kann selbst für einen riesigen Korpus mit hoher Geschwindigkeit lernen. Es scheint, dass er in etwa 30 Minuten einen Korpus von ungefähr 2 GB lernen konnte, was ein bz2-komprimiertes japanisches Wikipedia-Dokument ist.

Bis ich word2vec starte, der nichts über die Verarbeitung natürlicher Sprache weiß: Höchstwahrscheinlich Tagebuch

Ich habe LDA in der japanischen Wikipedia mit GenSim ausprobiert, aber ich erinnere mich, dass es damals einen halben Tag gedauert hat. Selbst wenn es in der Sprache C implementiert ist und die Maschinenspezifikationen höher sind als zu diesem Zeitpunkt, besteht kein Zweifel daran, dass word2vec überwältigend schneller ist.

Einführung in die Verarbeitung natürlicher Sprache mit GenSim, mit der Sie LSI und LDA einfach ausprobieren können - SELECT * FROM life;

GloVe

Wir haben gesehen, dass es Methoden gibt, die auf der Anzahl der SVD-ähnlichen Wörter basieren, und Ansätze, die sie wahrscheinlich wie word2vec behandeln, aber jede hat Vor- und Nachteile.

Methode basierend auf der Anzahl der Auftritte ―― Ein kleiner Korpus kann mit hoher Geschwindigkeit gelernt werden, aber ein großer Korpus braucht Zeit. ――Es wird verwendet, um die Ähnlichkeit von Wörtern zu messen, aber weniger häufig vorkommende Wörter können überproportional an Bedeutung gewinnen.
Wahrscheinlichkeitsbasierte Methode
Du musst einen großen Korpus haben.
Es können auch andere komplexe Muster als die Wortähnlichkeit gemessen werden.

Es gibt eine Methode namens GloVe, die die beiden Welten miteinander verbindet ([Richard Socher](http: // www), der für diese Vorlesung verantwortlich ist. Vorgeschlagen von einer Gruppe von .socher.org /) et al.

--Schnelles Lernen -Kann große Korpora handhaben

Kleiner Korpus, kleine Vektorleistung ist gut

[PYTHON] Vektordarstellung einfacher Wörter: word2vec, GloVe