[PYTHON] Untersuchen Sie die Auswirkung von Ausreißern auf die Korrelation
Heute habe ich Pandas verwendet, um auf Kapitel 10 "Auswirkungen von Ausreißern auf den Korrelationskoeffizienten" in Easy Statistics by R zu verweisen. Ich werde erklären, wie Ausreißer entfernt werden, während die Korrelation untersucht wird. Das ursprüngliche Buch verwendete R, aber Pandas können als Alternative verwendet werden, um auf einfache Weise eine auf Datenrahmen basierende Analyse in Python durchzuführen.
Untersuchen Sie das Tiergewicht und das Gehirngewicht
Wie im Originalbuch [Daten zu Tiergewicht und -gewicht](http://www.open.edu/openlearn/science-maths-technology/mathematics-and-statistics/mathematics/exploring-data-graphs-and- Verwenden Sie numerische Zusammenfassungen / Inhaltsabschnitt-2.7).
Zunächst habe ich diese Daten als CSV-Daten vorbereitet, damit sie sowohl vom Computer als auch [neulich] verarbeitet werden können (http://qiita.com/ynakayama/items/1a55ddbb85ae08970ad8) (https://github.com/ynakayama/sandbox/blob). /c4720fb8ff2973314e06e8cd2342b0e8e849889f/python/pandas/animal.csv).
Bringen Sie CSV-Daten in einen Datenrahmen.
animal = pd.read_csv('animal.csv')
Zeichnen Sie ein Streudiagramm und ermitteln Sie den Korrelationskoeffizienten
Wenn Sie zwei Variablen haben und deren Korrelation untersuchen möchten, müssen Sie sie zunächst in einem Streudiagramm betrachten. Das Zeichnen einer Streukarte erfolgt wie zuvor erläutert (http://qiita.com/ynakayama/items/2ec380ab1176e4569ebe). Ich werde es sofort versuchen.
plt.figure()
plt.scatter(animal.ix[:,1], animal.ix[:,2])
plt.savefig('animal.png')

Dann finden Sie den Korrelationskoeffizienten wie gewohnt.
animal.corr()
#=>
# Body weight (kg) Brain weight (g)
# Body weight (kg) 1.000000 -0.005341
# Brain weight (g) -0.005341 1.000000
Der Wert des Korrelationskoeffizienten -0,005 wurde wie auf Seite 250 des Originalbuchs angegeben erhalten. Bei dieser Rate gibt es fast keine Korrelation.
Ausreißer entfernen
Das Überprüfen des Ausreißers erfolgt wie zuvor erläutert (http://qiita.com/ynakayama/items/022b2d3d4a7f4adf1f31). Identifizieren und entfernen Sie den Ausreißer jedoch gemäß dem R-Code des Originalbuchs. Gehen. Erstens befindet sich oben im Streudiagramm oben nur ein Punkt. Dies ist ein Brachiosaurus-Dinosaurier namens Brachiosaurus mit der Nummer 24 in Daten und wiegt 80.000 kg. Die Daten zeigen, dass das Gehirn weniger als 1.000 g wiegt. Lassen Sie uns das loswerden.
#Wählen Sie nur Daten aus, die weniger als 80.000 wiegen
animal2 = animal[animal.ix[:,1] < 80000]
Dies bedeutet, dass Sie Daten auswählen, die weniger als 80.000 wiegen. Wenn Sie keine Indexreferenz hinzufügen, bleiben nur weniger als 80000 der Daten übrig, und die nicht zutreffenden Daten sind NaN. Selbst wenn Sie dies schreiben, ist das Ergebnis daher dasselbe.
animal2 = animal[animal < 80000].dropna()
Zeichnen Sie in diesem Zustand ein Streudiagramm und ermitteln Sie den Korrelationskoeffizienten.
animal2.corr()
#=>
# Body weight (kg) Brain weight (g)
# Body weight (kg) 1.000000 0.308243
# Brain weight (g) 0.308243 1.000000
Der Korrelationskoeffizient beträgt jetzt 0,30. Es wird eine etwas schwächere positive Korrelation geben. Entfernen wir dann wie im Originalbuch vier Tiere mit einem Gewicht von mehr als 2.000 kg.
animal2 = animal[animal.ix[:,1] < 2000]
animal2.corr()
#=>
# Body weight (kg) Brain weight (g)
# Body weight (kg) 1.000000 0.542351
#Brain weight (g) 0.542351 1.000000
plt.scatter(animal2.ix[:,1], animal2.ix[:,2])
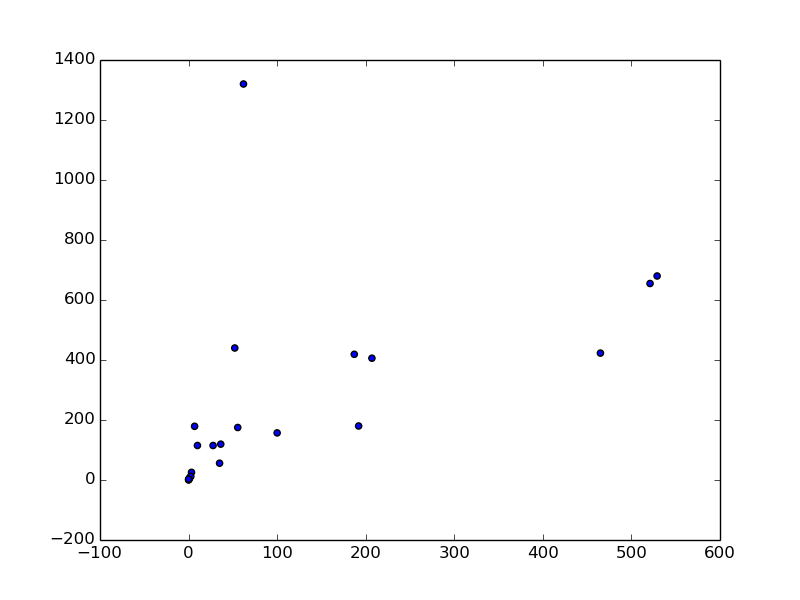
Diesmal ist der Korrelationskoeffizient auf 0,54 gestiegen. Sie können sehen, dass es oben links im Streudiagramm nur einen Ausreißer gibt. Es ist ein Mensch, der weniger als 100 kg wiegt und mehr als 1.200 g wiegt. Es ist ersichtlich, dass das Verhältnis von Gehirngewicht zu Körpergewicht beim Menschen im Vergleich zu anderen Tieren sehr hoch ist.
Was ist, wenn auch Menschen entfernt werden? Konzentrieren Sie sich auf Tiere mit einem Gewicht von weniger als 1.000 g und untersuchen Sie sie erneut.
animal3 = animal2[animal2.ix[:,2] < 1000]
#Finden Sie den Korrelationskoeffizienten
animal3.corr()
#=>
# Body weight (kg) Brain weight (g)
# Body weight (kg) 1.000000 0.882234
# Brain weight (g) 0.882234 1.000000

Der Korrelationskoeffizient beträgt 0,88. Daraus wurde festgestellt, dass mit Ausnahme einiger Tiere eine starke positive Korrelation zwischen Gehirngewicht und Gewicht besteht.
Führen Sie eine lineare Regression durch
Obwohl dies nicht im Originalbuch enthalten ist, haben wir eine starke positive Korrelation erhalten. Lassen Sie uns also die Regressionsgleichung finden.
from scipy import stats
stats.linregress(animal3.ix[:,1], animal3.ix[:,2])
#=> (1.0958855201992723,
# 68.659009180996094,
# 0.88223361379712761,
# 5.648035643926062e-08,
# 0.13077177749121441)
Die Rückgabewerte von scipy.stats.linregress werden wie in SciPy Documents gezeigt gekippt. , Abschnitt, Korrelationskoeffizient, P-Wert, Standardfehler.
Daher lautet die Regressionsgleichung (bis zur zweiten Minderheit) wie folgt.
y = 1.10x + 68.66
Sie können auch sehen, dass der P-Wert ein sehr kleiner Wert ist.
Zusammenfassung
Die beiden wichtigsten Datenanalysen unter Verwendung von Statistiken sind Hypothesentest und Korrelationsanalyse. Man kann mit Sicherheit sagen, dass es sich um Artikel handelt (f5f42b5d46b97009638b). (Natürlich gibt es andere, um es gelinde auszudrücken)
Neulich und dieses Mal haben wir eine sogenannte Korrelationsanalyse durchgeführt, aber die Überprüfung, ob es eine Korrelation zwischen zwei Variablen wie dieser gibt, ist die Grundlage der Statistik. Ich werde.
Indem Sie eine feste Hypothese darüber aufstellen, was als verwandt angesehen wird, und die Datenanalyse in Frage stellen, können Sie ein Ergebnis darüber erhalten, wie die Beziehung statistisch ist.
Das nächste Mal werde ich den Hypothesentest zusammenfassen, der zum ersten Mal seit langer Zeit eine weitere statistische Hauptmethode darstellt.
Recommended Posts