[PYTHON] Lernen Sie noch einmal die Grundlagen von Theano
Es ist "Theano", ein Rahmen für Deep Learning, aber ehrlich gesagt ist es ziemlich schwierig. Beim Lernen habe ich mit Bezug auf das ursprüngliche Tutorial und den japanischen Kommentar (auch in Qiita) gearbeitet, aber es ist schwer zu verstehen. Hier werden wir die Grundlagen von Theano noch einmal überprüfen, während wir einen kleinen Code verschieben. (Meine Umgebung ist momentan Python 2.7.8, theano 0.7.0.)
Verwendung von variablen-symbolischen und gemeinsam genutzten Variablen
In Theano werden sogenannte Variablen nicht direkt manipuliert, sondern Beziehungen werden durch Symbole beschrieben, die im Verarbeitungssystem hinterlegt sind, und die Eingabe / Ausgabe erfolgt, nachdem das Verarbeitungssystem sie nach Bedarf verarbeitet hat. Es ist ein Hauptmerkmal von Theano, dass die automatische Differenzierung der Gleichung in dieser "Verarbeitung" enthalten ist.
Verwenden wir zunächst eine normale symbolische Variable.
import theano
import theano.tensor as T
a = T.dscalar('a')
b = T.dscalar('b')
c = a + 2 * b
f_1 = theano.function([a,b], c)
Wenn Sie bis zu diesem Punkt eingeben und ausführen, werden Sie das Gefühl haben, dass die Festplatte ein rasselndes Geräusch macht und eine Zwischendatei generiert. Danach wird die definierte Funktion ausgeführt.
>>> f_1(2,3)
>>> array(8.0)
Bisherige Verwendung von symbolischen Theano-Variablen. Auszüge aus der Theano-Dokumentation und Listen verschiedener Variablentypen.
Theano Variables
| Variablentyp | Verfügbare Variablen |
|---|---|
| byte | bscalar, bvector, bmatrix, brow, bcol, btensor3, btensor4 |
| 16-bit integers | wscalar, wvector, wmatrix, wrow, wcol, wtensor3, wtensor4 |
| 32-bit integers | iscalar, ivector, imatrix, irow, icol, itensor3, itensor4 |
| 64-bit integers | lscalar, lvector, lmatrix, lrow, lcol, ltensor3, ltensor4 |
| float | fscalar, fvector, fmatrix, frow, fcol, ftensor3, ftensor4 |
| double | dscalar, dvector, dmatrix, drow, dcol, dtensor3, dtensor4 |
| complex | cscalar, cvector, cmatrix, crow, ccol, ctensor3, ctensor4 |
Wie oben erwähnt, gibt das erste Zeichen der Variablen% scalar und% vector die Bitlänge der Variablen an. Wenn dies weggelassen wird, sind der Standardwert "float" und die Bitlänge (Variablentyp, dtype) floatX-Typ (Typ, der in der Konfiguration festgelegt werden kann).
Eine andere Sache, an die Sie sich erinnern sollten, ist ** Shared Variable **. Symbolische Variablen sind in Theano eher "geschlossene" Variablen, während gemeinsam genutzte Variablen Variablen sind, auf die von mehreren Funktionen verwiesen wird und die für Dinge verwendet werden, die jedes Mal aktualisiert werden, z. B. Lernparameter. Verwenden wir diese gemeinsam genutzte Variable.
w = theano.shared(np.zeros(10), name='w')
print w.get_value()
Wie oben erwähnt, wird es durch theano.shared (Anfangswert, Symbolname in Theano) definiert. Im Gegensatz zu normalen symbolischen Variablen können gemeinsam genutzte Variablen mit "get_value ()" abgerufen werden. (Um den Wert einer symbolischen Variablen abzurufen, die keine gemeinsam genutzte Variable ist, muss umgekehrt eine Funktion für diesen Zweck vorbereitet werden.)
>>> print a # Theano Symbol
>>> a # I cannot see it
>>> print b # Theano Symbol
>>> b # I cannot see it...
>>> print w.get_value() # Theano Shared Variable
>>>[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
Wenn Sie eine gemeinsam genutzte Variable im Konstruktor deklarieren, können Sie "Borrow" angeben.
s_default = theano.shared(np_array) #Der Standardwert ist Ausleihen=False
s_false = theano.shared(np_array, borrow=False)
s_true = theano.shared(np_array, borrow=True)
Dies ist eine Option, die beim Erstellen einer gemeinsam genutzten Variablen keine Kopie erstellt. (Das ursprüngliche numpy-Objekt ist zerstört.) (Ich verstehe es noch nicht. Klicken Sie hier, um weitere Informationen zu erhalten. [Http://deeplearning.net/software/theano/tutorial/aliasing.html#borrowing-when-creating-shared. Siehe -Variablen).)
Theanos Funktion
Der wichtigste Teil von Theano. Lassen Sie uns zunächst einige Schreibstile zitieren. (Die vier Sätze sind irrelevant.)
>>> f = theano.function([x], 2*x)
>>> predict = theano.function(inputs=[x], outputs=prediction,
allow_input_downcast=True)
>>> linear_mix = theano.function([A, x, theano.Param(b, default=b_default)], [y, z])
>>> train = theano.function(
inputs=[x,y],
outputs=[prediction, xent],
updates=((w, w - 0.1 * gw), (b, b - 0.1 * gb)),
allow_input_downcast=True)
Wie oben erwähnt, wird theano.function () für eine lange Zeit beschrieben, je nachdem, wie Optionen hinzugefügt werden.
Das kürzeste Format ist wie folgt.
f = theano.function("Eingang", "Ausgabe")
List und Tupel werden also für mehrere Ein- und Ausgänge verwendet. (Es scheint, dass sogar eine Variable vom Skalartyp im Listenformat vorliegen muss, um die Eingabe anzugeben.) Das Folgende ist ein teilweiser Nachdruck der Erläuterung des Dokuments.
function.function(inputs, outputs, mode=None, updates=None, givens=None, no_default_updates=False, accept_inplace=False, name=None, rebuild_strict=True, allow_input_downcast=None, profile=None, on_unused_input='raise')
Parameters
- ** params **: Eingabewerte (erforderlich, Eingaben)
- ** Ausgänge **: Ausgabewerte (erforderlich)
- mode
- updates
- givens
- no_default_updates
- name
- rebuild_strict
- allow_input_downcast
- profile
** Aktualisierungen ** werden häufig zum Aktualisieren von Parametern verwendet, wie dies bei Optimierungsberechnungen der Fall ist. Unten finden Sie ein Beispiel für die Verwendung von Updates.
a = T.dscalar('a')
w2 = theano.shared(0.0, name='w2')
c = a + 2 * b + w2
f_3 = theano.function([a, b], c, updates=({w2: w2 + 1}))
#Oder f_3 = theano.function([a,b],c, updates=[(w2, w2 + 1)])
for i in range(5):
print f_3(2, 3)
>>>
8.0
9.0
10.0
11.0
12.0
Sie können sehen, dass der Inhalt von Updates bei jedem Aufruf der Funktion wiedergegeben wird.
** gibt ** wird verwendet, um einer Variablen einen konkreten numerischen Wert zuzuweisen. Insbesondere wird es verwendet, wenn der Funktion theano eine gemeinsam genutzte Variable zugewiesen wird. (Wenn Sie eine gemeinsam genutzte Variable mit ** Eingaben ** angeben, tritt ein Fehler auf.)
w1 = T.dscalar('w1')
c = a + w1 * b
f_2a = theano.function([a, b], c, givens=[(w1, -2.0)])
print f_2a(2, 3)
>>> -4.0 # OK, c=a + w1 *zu w1 von b-2.0 ist zugewiesen.
#Ein Fehler tritt auf, wenn in den Eingaben eine gemeinsam genutzte Variable angegeben wird.
w2 = theano.shared(-2.0, name='w2') #w2 ist eine gemeinsam genutzte Variable
f_2b = theano.function([a, b, w2], c) #Das erste Argument sind Eingaben
---------------------------------------------------------------------------
. . .
TypeError: Cannot use a shared variable (w2) as explicit input. Consider substituting a non-shared variable via the `givens` parameter
** allow_input_downcast ** wird verwendet, um die Typverwaltung zu lockern und Fehler in Situationen zu vermeiden, in denen die strikte Verwaltung von Variablentypen in Theano einen Fehler verursacht.
Finden Sie den Mindestwert (ohne T.grad ())
Ich möchte versuchen, den Mindestwert der Funktion mit den Funktionen zu finden, die wir bisher gesehen haben. Als Beispiel habe ich mit der Funktion $ y = (x-1) ^ 4 $ einen Code ausgeführt, der das Ausmaß der Änderung in y überwacht, während x geändert wird, und eine iterative Berechnung durchführt, bis die Änderung unter einen vorbestimmten Schwellenwert fällt. (Da kein Differenzwert verwendet wird, handelt es sich nicht um eine Gradientenmethode.)
x_init = -1.0
x = theano.shared(x_init, name='x')
y = T.dscalar('y')
y = (x - 1.) ** 4
#Funktion f_4()Ist definiert. Der Inkrementwert von x wird durch Aktualisierung angegeben.
f_4 = theano.function([], y, updates=({x: x + 0.01}))
# into loop
iter = 1000
y_prev = (x_init -1.1) ** 4
eps = 1.e-6
for i in range(iter):
y_update = f_4() ####In Loop, f_4()Anruf.
y_delta = np.abs(y_update - y_prev)
if y_delta < eps:
x_min = x.get_value()
break
y_prev = y_update
print 'x_min = ', x_min
>>> x_min = 0.98999995552
Wie erwartet haben wir x_min berechnet, was den Minimalwert der Funktion $ y = (x-1) ^ 4 $ ergibt. Ich habe x nicht explizit für die Funktion f_4 eingegeben, aber ich kann sehen, dass die Option ** Updates ** ordnungsgemäß funktioniert.
Versuchen Sie es mit der automatischen Differenzierung T.grad ()
Schließlich ist es T.grad (), das ein Merkmal von theano ist.
x = T.dscalar('x')
y = (x - 4) * (x ** 2 * 2+ 6) #Differenzierte Formel
#Differenziere y in Bezug auf x
gy = T.grad(cost=y, wrt=x)
#Definieren Sie eine Funktion, um den Differentialkoeffizienten zu ermitteln,Eingang:x,Ausgabe: gy
f = theano.function(inputs=[x], outputs=gy)
print theano.pp(f.maker.fgraph.outputs[0])
#
print f(0)
print f(1)
print f(2)
>>>
((TensorConstant{1.0} * (((x ** TensorConstant{2}) * TensorConstant{2}) + TensorConstant{6})) + ((((TensorConstant{1.0} * (x - TensorConstant{4})) * TensorConstant{2}) * TensorConstant{2}) * (x ** TensorConstant{1})))
6.0
-4.0
-2.0
Wie oben erwähnt, kann das Ergebnis der Differenzierung der durch print theano.pp (...) angegebenen Formel angezeigt werden. Zusätzlich kann der y-Differenzwert an jedem x (= 0, 1, 2) berechnet werden. Überprüfen Sie vorerst die Parameter, die im Dokument angegeben werden können.
theano.gradient.grad(cost, wrt, consider_constant=None, disconnected_inputs='raise', add_names=True, known_grads=None, return_disconnected='zero', null_gradients='raise')
Parameters:
- ** Kosten **: Zu differenzierende Formel (erforderlich)
- ** wrt **: Differenzkoeffizient (erforderlich)
- consider_constant
- disconnected_inputs
- add_name
- known_grads
- return_disconnected
- null_gradients
Kosten und Wrt sind erforderliche Parameter.
Gradientenabstieg implementieren
Nachdem ich die erforderlichen Teile besser verstanden habe, werde ich die Gradientenabstiegsmethode implementieren. Die Zielfunktion ist die Rosenbrock-Funktion, die (wahrscheinlich) häufig in Benchmarking-Algorithmen wie der Gradientenmethode verwendet wird.
Fig. Rosenbrock Function
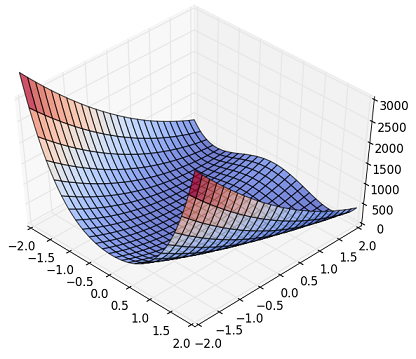
Obwohl es in der obigen Figur schwer zu sehen ist, hat es eine Nichtlinearität, dass es eine Rille im Ring gibt und Z plötzlich ansteigt, wenn es vom peripheren Teil abweicht. (Es gibt eine schöne Figur auf Wikipedia, also beziehen Sie sich bitte darauf, wenn Sie interessiert sind.)
Die Formel lautet wie folgt.
f(x, y) = (a - x)^2 + b * (y - x^2)^2
\ \ \ \\usually \ a\ = 1,\ and\ b\ =100
Diese Funktion hat $ (x, y) = (a, a ^ 2) $ und ein globales Minimum von $ f = 0.0 $. Der folgende Code wurde erstellt und ausgeführt.
import numpy as np
import theano
import theano.tensor as T
# Prep. variables and function
x_init = np.array([2.0, 2.0])
x = theano.shared(x_init, name='x')
a, b = (1., 100.)
# z_rb = (a - x) ** 2 + b * (y - x **2) **2
z_rb = (a - x[0]) ** 2 + b * (x[1] - x[0] **2) **2
dx = T.grad(cost=z_rb, wrt=x)
# Compile
train = theano.function(
inputs=[],
outputs=[z_rb],
updates=[(x, x-0.001 *dx)]
)
# Train
steps = 10000
print '(x,y)_init = (%9.3f, %9.3f)' % (x_init[0], x_init[1])
for i in range(steps):
z_tmp = train()
x_fin = x.get_value()
print '(x,y)_final= (%9.3f, %9.3f)' % (x_fin[0], x_fin[1])
>>>
(x,y)_init = ( 2.000, 2.000)
(x,y)_final= ( 1.008, 1.016)
Die Parameter (x, y) sind in einem Vektor x [] der Länge 2 zusammengefasst. Ausgehend vom Anfangswert x = [2.0, 2.0] konnten wir einen Wert nahe der theoretischen Lösung (1, 1) erhalten. Die folgende Abbildung zeigt die Geschichte von x [](x, y).
Fig. Rosenbrock Function, contour

Es ist zu sehen, dass es zuerst von (2., 2.) nach links geschwenkt wird und dann in die Ringnut fällt. (Als ich mit den Anfangswerten (3., 3.) berechnete, ging es zunächst wunderbar auseinander ... Übrigens ist der Code von Numpy + scipy.optimize, der Theano nicht verwendet, der Anfangswert (3). , 3.) konnte auch die konvergente Lösung finden. Es scheint, dass sie eher mit dem optimalen Lösungssuchalgorithmus zusammenhängt als mit der Frage, ob Theano verwendet wird oder nicht.)
Wenn Sie dies bisher verstanden haben, können Sie die Bewegung des Referenzcodes sehen, der im Theano-Lernprogramm angezeigt wird. (Eigentlich habe ich ein einfaches Programm für die logistische Regression erstellt und es ausprobiert.) In letzter Zeit ist "Chainer" populär geworden, und die Anzahl der Leute, die "Theano lernen" möchten, nimmt möglicherweise ab. Der erste Artikel zum Thema Deep Learning in Übersee, der sich mit Theano befasst, wird jedoch weiterhin erscheinen, und PyMC3 der MCMC-Implementierungsbibliothek basiert ebenfalls auf Theano. Daher halte ich es für wichtig, das Verständnis von Theano zu vertiefen. Es gibt.
Referenzen (Website)
- Theano Documentation http://deeplearning.net/software/theano/#documentation
- [Qiita] Theanos grundlegendes Memo http://qiita.com/mokemokechicken/items/3fbf6af714c1f66f99e9
- Theanos Implementierung einer logistischen Regression in zwei Klassen, ein Durchbruch bei der künstlichen Intelligenz http://aidiary.hatenablog.com/entry/20150519/1432038633
- Dokumentation zur SciPy-Optimierung http://docs.scipy.org/doc/scipy/reference/tutorial/optimize.html
- Wikipedia, Rosenbrock function https://en.wikipedia.org/wiki/Rosenbrock_function
Recommended Posts