[PYTHON] [Computer Vision] Epipolare Geometrie mit Katzen gelernt

Einführung

Die Katze ist süß ~

In diesem Artikel lernen wir mit Katzen ** die Technologie zur Wiederherstellung der 3D-Welt aus Bildern mit mehreren Blickwinkeln kennen, die im Bereich der Bildverarbeitung behandelt wird **.

Dieses Gebiet wird noch erforscht und manchmal kommen schwierige Formeln heraus, aber ich hoffe, dass der Schmerz durch das Lernen mit Katzen neutralisiert wird.

Dieser Artikel entspricht Kapitel 5, "5.1 Epipolare Geometrie, 5.2 Berechnungen mit Kameras und 3D-Strukturen" in "Practical Computer Vision". Machen.

Ich möchte die 3D-Welt aus einem Bild mit mehreren Ansichten wiederherstellen

Das Bild der Katze am Anfang war ein zweidimensionales Bild. Wie stellen Sie die dreidimensionale Form dieser Katze wieder her?

Die richtige Antwort ist ** aus mehreren Perspektiven zu schießen, während Sie die Kamera auf die Katze zu bewegen **.

Basierend darauf, wie die Katze von jedem Standpunkt aus aussieht, werden die Änderung der Haltung der Kamera und die geometrische Struktur der Katze, die von der Kamera fotografiert wird, umgekehrt berechnet.

Dies wird als Struktur aus Bewegung (SfM) bezeichnet.

Das Verfahren ist wie folgt.

• ** 1. Finde einen entsprechenden Punkt ** Entsprechende Punkte sind beispielsweise zwei Punkte, die in jedem Bild erscheinen, wenn die Hand der Katze aus verschiedenen Perspektiven betrachtet wird. Wenn Sie die entsprechenden Punkte im Bild vor und nach dem Verschieben des Ansichtspunkts finden, erhalten Sie einen Hinweis darauf, wie Sie sich bewegt haben.

• ** 2. Kamerabewegung schätzen ** Schätzen Sie, wie sich der Ansichtspunkt bewegt hat, und verwenden Sie die entsprechenden Punkte als Hinweise.

• ** 3. Rekonstruiere die 3D-Szene ** Die dreidimensionale Form wird basierend auf den entsprechenden Punkten und dem Bewegungsschätzungsergebnis der Kamera wiederhergestellt.

• ** 4. Gesamtoptimierung ** Durch Wiederholen der Schritte 2 und 3 bei jeder Bewegung der Kamera häufen sich Fehler bei der Kamerabewegung / Wiederherstellung von 3D-Szenen. Um dies zu lösen, wird die Gesamtgenauigkeit verbessert, indem die optimale Lösung gefunden wird, die den Fehler zwischen dem gemessenen Wert und dem geschätzten Wert unter Verwendung aller entsprechenden Punkte und der Schätzergebnisse der Blickpunktbewegung minimiert.

Betrachten Sie hier Bildpaare, um das Problem zu vereinfachen. Mit anderen Worten, betrachten Sie nur zwei Gesichtspunkte.

Zunächst erkläre ich die grundlegende Theorie, die zwischen diesen Bildern auftritt. Danach werden wir die Kamerabewegung abschätzen und die 3D-Szene rekonstruieren. Die Gesamtoptimierung von 4. ist ein Prozess, der nur erforderlich ist, wenn es viele Gesichtspunkte gibt, daher werden wir ihn hier nicht berücksichtigen.

Epipolare Geometrie ist was?

Bevor Sie die Kamera bewegen oder eine 3D-Szene aus einem Bild mit zwei Ansichten wiederherstellen, müssen Sie die grundlegende Theorie der epipolaren Geometrie verstehen. Epipolare Geometrie ist die Geometrie, die auftritt, wenn zwei Kameras dasselbe dreidimensionale Objekt aus verschiedenen Perspektiven erfassen.

Die Elemente, die die epipolare Geometrie systematisieren, sind die Epipolarebene, die Epipolarlinien, die Epipole, die Grundmatrix und die Grundmatrix, die wir als nächstes einführen werden.

Fünf super wichtige Wörter, die in der epipolaren Geometrie vorkommen

• ** Epipolare Ebene ** (blaue Ebene in der Abbildung) Angenommen, die optischen Zentren der beiden Kameras sind $ O_ {1} $ und $ O_ {2} $, die dreidimensionalen Punkte $ X $, $ O_ {1} $, $ O_ {2} $, insgesamt drei Punkte Die Ebene, durch die es geht, wird als epipolare Ebene bezeichnet. Das blaue Flugzeug in der Figur.

• ** Epipolare Linie ** (gelbe Linie in der Abbildung) Eine Epipolarlinie ist eine Linie, in der sich die Epipolarebene und jede Bildebene schneiden. Wenn beispielsweise ein dreidimensionaler Punkt X als Punkt x1 in Bild 1 erscheint, erscheint derselbe Punkt X irgendwo auf der Epipolarlinie in Bild 2.

• ** Epipol ** (roter Punkt in der Abbildung) Die epipolaren Linien aller Bilder schneiden sich immer an einem Punkt. Das ist Epipole. Daher verlaufen alle epipolaren Linien durch Epipole. Dieser Punkt ist der Punkt, an dem die Kameramitte des anderen Bildes auf Ihr Bild projiziert wird.

Entsprechende Punkte und epipolare Linien auf dem tatsächlichen Bild:

• ** Grundmatrix ** Es ist eine 3x3-Matrix und enthält ** interne / externe Matrixinformationen der Kamera. ** Es hat auch die Aufgabe, ** einen Punkt (Dimension 0) auf einem Bild einer Epipolarlinie (Dimension 1) auf einem anderen Bild zuzuordnen. Wenn diese Matrix geschätzt werden kann, kann sie später beim Schätzen der Kamerabewegung usw. verwendet werden. Daher ist es sehr wichtig, diese Matrix korrekt zu finden. Schauen wir uns das als nächstes genauer an.

• ** Essentielle Matrix ** Ähnlich im Namen der Basismatrix, jedoch ein Verwandter der Basismatrix. Es ist eine 3x3-Matrix und enthält ** externe Matrixinformationen der Kamera. ** Sie können $ F $ mit der kamerainternen Matrix $ K $ in $ E = K_ {2} FK_ {1} $ konvertieren.

Grundmatrix F.

Auftreten einer epipolaren Zurückhaltungszeremonie

Wenn $ x_ {1} $ und $ x_ {2} $ Korrespondenzpunkte sind, gilt die folgende Beziehung für alle Korrespondenzpunkte $ x_ {1} $, $ x_ {2} $.

\boldsymbol{x_{2}^{T}}F\boldsymbol{x_{1}} = 0

$ F $ heißt Basismatrix und ist eine 3x3-Matrix. $ x_ {1} $, $ x_ {2} $ sind dreidimensionale Vektoren, die die Koordinaten der entsprechenden Punkte im ** Bildkoordinatensystem im simultanen Koordinatensystem darstellen.

Diese Formel zeigt, dass zwischen den entsprechenden Punkten der beiden Bilder eine Einschränkungsbeziehung besteht. ** Diese Formel wird als epipolare Rückhalteformel bezeichnet. ** Sobald der Ansichtspunkt festgelegt ist, wird entschieden (= Einschränkung), auf welcher Seite in Bild 2 sich der entsprechende Punkt in Bild 1 befindet. Und diese Einschränkungsformel hängt nur von ** 2 Gesichtspunkten ab und überhaupt nicht von der 3D-Szene. ** ** **

Lassen Sie uns nun überprüfen, ob $ \ boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}} = 0 $ gilt.

Da $ x_ {1} $ ein Punkt in Bild 1 ist, wird er ausgedrückt als $ x_ {1} = (x_ {1}, y_ {1}, z_ {1}) ^ {T} $ ($ z_ {1) } $ Ist 1).

Da F eine 3x3-Matrix ist, ist $ Fx_ {1} $, das Produkt von $ x_ {1} $, ein dreidimensionaler Vektor. Sei dieser Vektor $ Fx_ {1} = (a, b, c) ^ T $.

Dieses $ Fx_ {1} = (a, b, c) ^ T $ ist der Koeffizient der Epipolarlinie in Bild 2. Das Multiplizieren dieses Koeffizienten mit x2 auf der Epipolarlinie zeigt dann, dass die lineare Gleichung $ ax + mit + c = 0 $ erfüllt ist. Mit anderen Worten, $ \ boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}} = 0 $ gilt!

Im Gegenteil, wenn das Ergebnis der Ersetzung von $ x_ {2} $ nicht 0 ist, kann gesagt werden, dass der Punkt $ x_ {2} $ nicht der entsprechende Punkt von x1 ist (siehe die folgende Abbildung).

Bei der Suche nach dem entsprechenden Punkt $ x_ {2} $ in Bild 2 des Punktes $ x_ {1} $ in Bild 1, anstatt nach dem gesamten Bild in ** Bild 2 zu suchen, $ x_ {1} $ Es muss nur die auf Bild 2 projizierte Epipolarlinie $ l_ {2} $ durchsucht werden **, damit sich die Berechnungskosten und die Fehlerantwortrate verringern.

Übrigens bildet die obige Gleichung $ \ boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}} = 0 $ den Punkt $ x_ {1} $ auf Bild 1 auf Bild 2 als gerade Linie ab. Es repräsentiert den Fall. Wenn im Gegensatz dazu der Punkt $ x_ {2} $ auf Bild 2 als gerade Linie auf Bild 1 abgebildet wird, wird die folgende Gleichung erhalten und beide Seiten werden transponiert, so dass es mathematisch gleich ist. ($ (\ Boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}}) ^ {T} = $ Die folgende Formel)

\boldsymbol{x_{1}^{T}}F^{T}\boldsymbol{x_{2}} = 0

Der Punkt ist, dass die Positionen von $ x_ {1} $ und $ x_ {2} $ vertauscht und F transponiert werden.

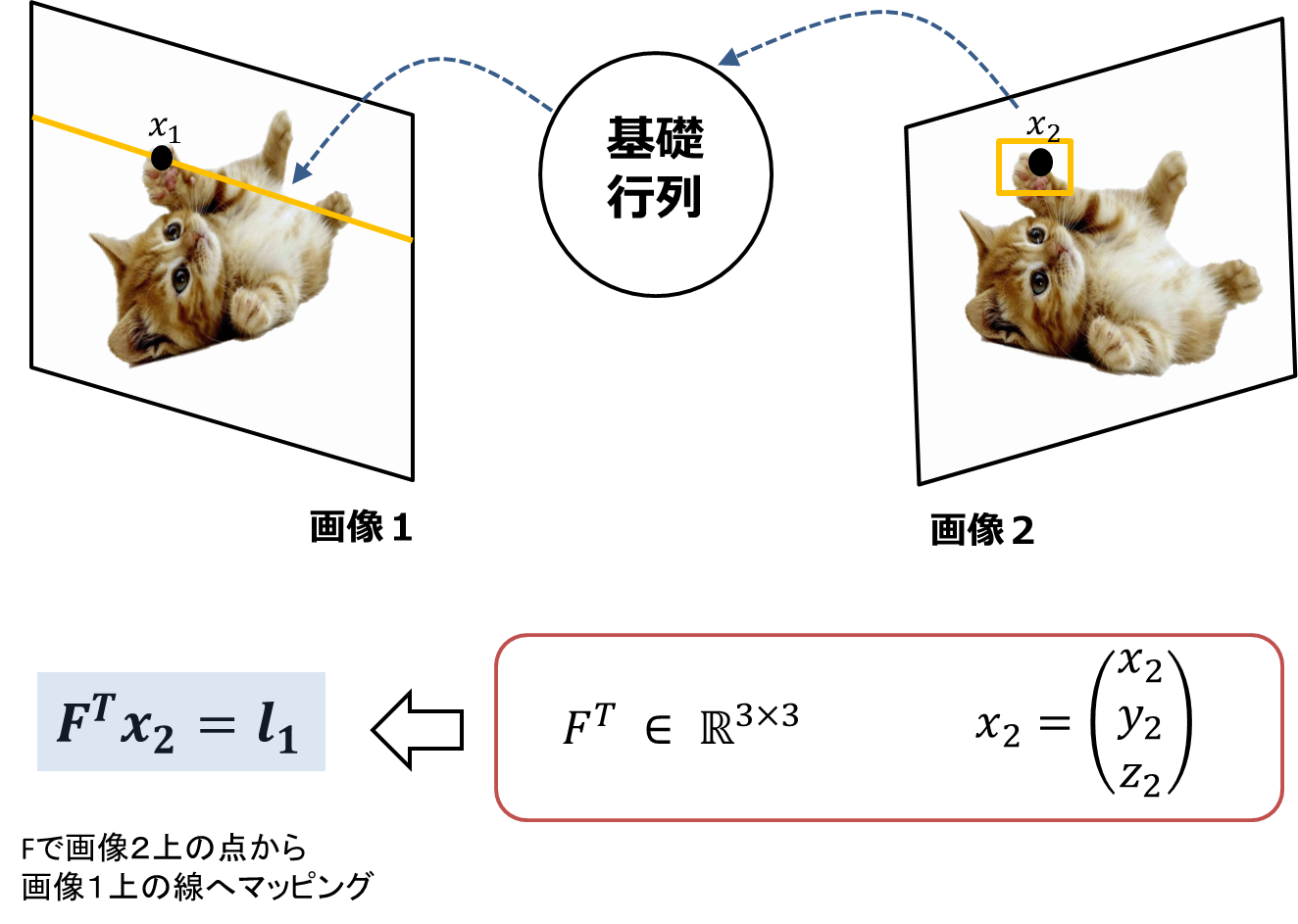
1. Finden Sie F.

Wie findest du F? Dafür gibt es mehrere typische Methoden.

• ** 8-Punkt-Algorithmus ** Schätzen Sie F mit 8 oder mehr entsprechenden Punkten. Lösen Sie mit der Methode der kleinsten Quadrate mit SVD. Verwenden Sie für den praktischen Gebrauch den normalisierten 8-Punkt-Algorithmus.

• ** Normalisierter 8-Punkt-Algorithmus ** Eine verbesserte Version des 8-Punkt-Algorithmus. Als Normalisierungsprozess wird der Ursprung zum Schwerpunkt der Punktgruppe der entsprechenden Punkte verschoben, und der durchschnittliche Abstand vom Schwerpunkt zu jedem entsprechenden Punkt wird auf $ \ sqrt2 $ eingestellt, so dass die Genauigkeit erheblich verbessert wird. [Normalisierte 8-Punkt-Algorithmus-Implementierung] (http://www.peterkovesi.com/matlabfns/Projective/fundmatrix.m) Normalisierungsimplementierung

• ** Algebraische Kostenminimierung (Wiederholung) ** Genauer als der normalisierte 8-Punkt-Algorithmus.

• ** Minimieren Sie den Fehler im Abstand zwischen dem Beobachtungspunkt und dem Schätzpunkt ** Nachdem Sie mit der obigen Methode F als Anfangswert angegeben haben, berechnen Sie einmal die Position von X und projizieren Sie sie auf das Bild. Minimieren Sie den Abstand (Fehler) zwischen dem Beobachtungspunkt und dem Schätzpunkt als Kostenfunktion. Es soll der Gold-Standard-Algorithmus sein und die höchste Genauigkeit aufweisen.

Wenn Sie die beiden Kameramatrizen kennen, finden Sie sie auch dort Implementierung.

8-Punkt-Algorithmus

Hier finden Sie eine Übersicht über den grundlegendsten 8-Punkt-Algorithmus (eine detaillierte Implementierung finden Sie unter dem obigen Link).

Der epipolare Einschränkungsausdruck $ \ boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}} = 0 $ gibt eine Gleichung für jeden Korrespondenzpunkt i:

Da die unbekannte Variable hier eine F-Matrix ist, werden wir F zusammenfassen und in Form der Gleichung Af = 0 nach f auflösen. Hier ist F eine 3x3-Matrix, aber da die Skala unbestimmt ist, kann sie gelöst werden, wenn es praktisch 8 entsprechende Punkte gibt. Der Name des "8-Punkt-Algorithmus" stammt von hier.

Verwenden Sie nach dem Zerlegen mit SVD, dass F Rang 2 ist. Wenn die minimale Singularität der diagonalen Komponente von Σ auf 0 gesetzt und gelöst wird, erhöht sich die Genauigkeit von F. Die linke Seite der folgenden Abbildung ist der Fall, in dem die Einschränkung von Rang 2 nicht angewendet wird, und die rechte Seite ist der Fall, in dem die Einschränkung von Rang 2 angewendet wird.

Zitiert aus Lit. [1].

2. Suchen Sie die Kameramatrix aus F.

Warum haben wir F gefunden? Weil wir die Kameramatrix P aus ** F ** finden können.

Wie bereits erwähnt, enthält F eine interne Kameramatrix und eine externe Kameramatrix. Wenn daher F in interne und externe Kameramatrizen zerlegt wird, kann die Kameramatrix daher aus F geschätzt werden.

Die Genauigkeit der Schätzung hängt jedoch davon ab, ob die Kamera im Voraus kalibriert wurde oder nicht. Wenn die internen Parameter der Kamera unbekannt sind, kann nur die Projektionstransformation aus F geschätzt werden.

Der Prozessablauf von F zur Schätzung der Kameramatrix ist in der folgenden Abbildung dargestellt.

Wenn die Kamera nicht kalibriert ist

Wenn die Kamera nicht kalibriert ist, dh wenn die internen Parameter der Kamera unbekannt sind, müssen sowohl die internen als auch die externen Parameter der Kamera geschätzt werden. In diesem Fall ** kann die Kameramatrix nur bis zur Projektionstransformation geschätzt werden. ** ** **

Normalerweise kann P zu F als eins berechnet werden, aber ** im Gegenteil, F zu P kann nicht als eins berechnet werden **. Dies liegt daran, dass die Grundmatrizen der beiden Sätze projizierter Bilder gleich sind.

Zum Beispiel sind F in der Kameramatrix (P, P'H) und F in der Kameramatrix (PH, P'H) gleich.

Die Kameramatrix $ P_ {1} $, $ P_ {2} $ ist wie folgt. × ist das äußere Produkt.

P_{1}=[I|0]Und P_{2} =[[e_{2}]×F|e_{2}]

Wenn die Kamera kalibriert wurde

Wenn die Kamera kalibriert wurde, müssen Sie nur die externen Parameter der Kamera schätzen. Alle Parameter mit Ausnahme der Translationsskala können geschätzt werden. F hat die Mehrdeutigkeit der Projektionstransformation, während E die Mehrdeutigkeit hat, vier Lösungen zu haben.

Finden Sie zuerst die Basismatrix E aus F mit $ E = K_ {2} FK_ {1} $. Als nächstes zerlegen Sie E mit SVD. Da E det (E) = 0 hat und die anderen Singularwerte als 0 gleich sind und ihre Größen unbestimmt sind, kann die diagonale Komponente von Σ als (1,1,0) geschrieben werden. Mit anderen Worten kann es durch SVD wie folgt zerlegt werden.

E=Udiag(1,1,0)V^{T}

$ u_ {3} $ ist der Vektor der dritten Spalte von $ U $

W = \begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1 
\end{pmatrix}

Am Ende erscheinen dann die folgenden vier Lösungen in der Kameramatrix.

Von diesen hat nur einer die Szene vor der Kamera, daher ist (a) die richtige Lösung. (Abbildung unten)

Zitiert aus Lit. [1].

3. Erstellen Sie die 3D-Welt neu

Die Kameramatrix P wurde erhalten. Lassen Sie uns endlich die dreidimensionale Welt rekonstruieren.

Dreieckige Vermessung

Die dreieckige Vermessung schätzt X, das gleichzeitig die folgenden Kamerakonvertierungsformeln aus zwei Blickwinkeln erfüllt.

Zitiert aus Lit. [1].

Aus der Kamerakonvertierungsformel, in der die Kameramatrix $ P_ {1} $, $ P_ {2} $ lautet

\lambda_{1}x_{1} = P_{1}X

\lambda_{2}x_{2} = P_{2}X

Wenn Sie es also in einer Matrix ausdrücken,

\begin{bmatrix}
P_{1} & -x_{1} & 0 \\
P_{2} & 0 & -x_{2} 
\end{bmatrix}
\begin{bmatrix}
X \\
\lambda_{1}\\
\lambda_{2} 
\end{bmatrix}
=0

Es wird sein.

Da dies auch in Form von Ax = 0 vorliegt, kann 3D X durch Lösen von x mit SVD wiederhergestellt werden.

Implementierung

• ykoga/cv_tutorial_epipolar (OpenCV)
• Ab OpenCV3.1 (veröffentlicht am 12.12.2015) wurde das sfm-Modul mit der Funktion Structure From Motion hinzugefügt.

Referenzmaterial

• Bücher [1] Multiple View Geometry in Computer Vision
  [2] Praktisches Computer Vision
• Implementierung MATLAB and Octave Functions for Computer Vision and Image Processing
• Bild Pakutaso GATAG ｜ Kostenlose Sammlung von Bild- / Fotomaterial 3.0
• Andere Fundamental Matrix Song