[PYTHON] Reihenfolge der Argumente für RegularGridInterpolator und interp2d

Es ist ein Memorandum von Mist.

scipy.interpolate.RegularGridIch bin immer verwirrt von der Reihenfolge der Argumente von Interpolator und der Spezifikation des Rasters, also habe ich den Testcode geschrieben. Der Grund für die Verwirrung ist, dass scipy.interpolate.interp2d usw. eine andere Reihenfolge von Argumenten zu haben scheinen.

Nein, die Argumente für das interp2d-Raster sind zwei eindimensionale Arrays, und das erste Argument für den RegularGridInterpolator ist ein mehrdimensionales Array, oder? Wenn Sie sagen, dass die Dinge anders sind, ist das richtig, und im Fall eines mehrdimensionalen Arrays ist die Form (n, m, l), wenn x (l), y (m), z (n). Ich habe keine Worte, die ich zurückgeben könnte, aber ich schreibe es einfach in umgekehrter Reihenfolge. <Schwache Warteschlange von vor langer Zeit

Also betete ich, dass ich beim nächsten Mal keinen Fehler machen würde, wenn ich mich auf diese Weise schäme.

import numpy as np
from scipy.interpolate import RegularGridInterpolator

x_iter = np.array([0,1,2,3,4])
y_iter = np.array([5,6,7])
z_iter = np.array([8,9])
print("number of x_iter l = %d" % (len(x_iter)))
print("number of y_iter m = %d" % (len(y_iter)))
print("number of z_iter n = %d" % (len(z_iter)))

def data_func(x, y, z) :
    return x + y*10 + z*100

data = []
for z in z_iter :
    buf2 = []
    for y in y_iter :
        buf = []
        for x in x_iter :
            buf.append(data_func(x, y, z))
        buf2.append(buf)
    data.append(buf2)

data = np.array(data)
print("data", data)
print("shape of data, n x m x l array", data.shape)

data_grid = tuple([z_iter, y_iter, x_iter])
print("data grid with a format tuple(z_iter, y_iter, x_iter) is", data_grid)
f = RegularGridInterpolator(data_grid, data)

point_of_interest = tuple([8.3, 5.5, 1.1])
print("point_of_interest with a format tuple(z, y, x) is", point_of_interest)
interp_value = f(point_of_interest)

print("interpolated value is", interp_value)

import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
from matplotlib import colors

figid = 1
plt.figure(figid)
ax1 = plt.subplot(1, 1, 1)
xx, yy = np.meshgrid(x_iter, y_iter)

data_2D = data[0, :, :]
print("shape of data_2D for z_bin = 0", data_2D.shape)
phist = ax1.pcolormesh(xx, yy, data_2D, norm=colors.Normalize())
plt.colorbar(phist)
ax1.set_ylabel("y")
ax1.set_xlabel("x")
plt.savefig("interp_test.png ")

Achten Sie beim Erstellen von Daten beim Drehen mit for auf die Reihenfolge des Drehens. Wenn Sie in der Standardeinstellung einen Wert außerhalb des Bereichs für die x-, y- und z-Werte angeben, tritt ein Fehler auf. Dieses Verhalten kann mit dem Argument bounds_error und der Variablen fill_value gesteuert werden (Standard ist bounds_error = True, fill_value = nan).

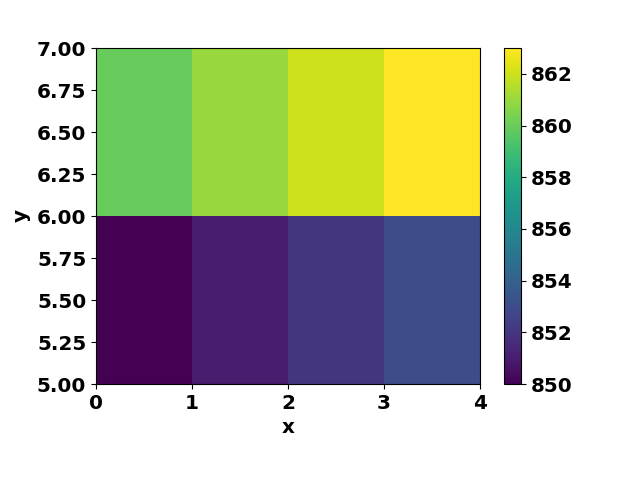
Übrigens sieht es bei Verwendung von scipy.interpolation.interp2D so aus. Wenn Sie standardmäßig einen Wert außerhalb des Bereichs für die x- und y-Werte angeben, sterben Sie nicht (gibt den Endwert in der Datentabelle zurück). Dieses Verhalten kann mit dem Argument bounds_error und der Variablen fill_value gesteuert werden (Standard ist bounds_error = False, fill_value = None).

import numpy as np
from scipy.interpolate import interp2d

x_iter = np.array([0,1,2,3,4])
y_iter = np.array([5,6,7])
print("number of x_iter l = %d" % (len(x_iter)))
print("number of y_iter m = %d" % (len(y_iter)))

def data_func(x, y) :
    return x + y*10

data = []
for y in y_iter :
    buf = []
    for x in x_iter :
        buf.append(data_func(x, y))
    data.append(buf)

data = np.array(data)
print("data", data)
print("shape of data, m x l array", data.shape)

# order of arguments: x-axis, y-axis, data
f = interp2d(x_iter, y_iter, data)

x = 1.5
y = 5.5
print("datapoint is (%f, %f), data_func(%f, %f) is %f" % (x, y, x, y, data_func(x, y)))
interp_value = f(x, y)
print("interpolated value is", interp_value)

# test2 : what happens if x1 is out of range?
x1 = 7 # x-range is (0, 4)
y1 = 10 # y-range is (5, 7)
print("datapoint is (%f, %f), data_func(%f, %f) is %f" % (x1, y1, x1, y1, data_func(x1, y1)))
interp_value = f(x1, y1)
print("interpolated value is", interp_value)
# this value is 
print("interpolated value for (%f, %f) is %f" % (x_iter[-1], y_iter[-1], f(x_iter[-1], y_iter[-1])))

import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as plt
from matplotlib import colors

figid = 1
plt.figure(figid)
ax1 = plt.subplot(1, 1, 1)
xx, yy = np.meshgrid(x_iter, y_iter)

phist = ax1.pcolormesh(xx, yy, data, norm=colors.Normalize())
plt.colorbar(phist)
ax1.set_ylabel("y")
ax1.set_xlabel("x")
plt.savefig("interp_test2D.png ")