[PYTHON] [Statistiques] Premier "écart-type" (pour éviter d'être frustré par les statistiques)
Pour ceux qui veulent apprendre des statistiques à partir de maintenant, je pense que «l'écart type» est un concept très important mais difficile à comprendre. Je le connais jusqu'à la «moyenne», et je pense que cela ressemble à «je comprends», mais «l'écart type» qui apparaît soudainement.
\sigma = \sqrt{ {1 \over n} \sum_{i=1}^n(x_i - \bar{x})^2}
Mur de. Je pense que certaines personnes ont été dépassées par le fait que «les maths sont impossibles» ici.
Si vous postez d'abord l'image du graphique, la longueur de la ligne rouge ci-dessous correspond à «l'écart type». Nous clarifierons également pourquoi cette longueur est l'écart type.
 (code is here)
(code is here)
Dans cet article, j'expliquerai quel est l'écart-type de 1 afin que même ceux qui ne sont pas bons en mathématiques puissent le comprendre. Je vais l'expliquer pour que même ceux qui comprennent la formule mais ne comprennent pas la signification de «l'écart type» puissent la comprendre intuitivement, alors jetez un œil.
(* Dans cet article, $ n $ est utilisé comme dénominateur de l'écart type. Dans certains cas, $ n-1 $ est utilisé, et il est utilisé correctement selon le cas à analyser. Je vais expliquer en utilisant n $.)
</ i> 0. À propos des symboles
Si vous n'êtes pas familier avec les mathématiques, la première chose qui vous trébuche est le symbole des mathématiques. Qu'est-ce que "$ x_i $"?
\sum_{i=1}^n x_i
Ceci est une explication pour ceux qui sont rafraîchissants. Si vous êtes d'accord avec les symboles mathématiques ici, veuillez passer à [Section suivante](http://qiita.com/kenmatsu4/items/e6c6acb289c02609e619#1 Moyenne tout d'abord).
Commençons par $ x_i $.
Tout le monde utilise Excel, non? Tout d'abord, supposons que vous ayez des données pour un tel test.
| Nom | Math |
|---|---|
| Tanaka:smile: | 96 |
| Takahashi:flushed: | 63 |
| Suzuki:stuck_out_tongue: | 85 |
| Watanabe:stuck_out_tongue_winking_eye: | 66 |
| Shimizu:laughing: | 91 |
| Kimura:grin: | 89 |
| Yamamoto:smirk: | 77 |
Au total
Score total=Tanaka(Math) +Takahashi(Math) +Suzuki(Math) +Watanabe(Math) +Shimizu(Math) +Kimura(Math) +Yamamoto(Math)
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
Peut être calculé comme.
Si l'ID est utilisé à la place du nom
| ID | Math |
|---|---|
| 1 | 96 |
| 2 | 63 |
| 3 | 85 |
| 4 | 66 |
| 5 | 91 |
| 6 | 89 |
| 7 | 77 |
Score total= {\rm ID}:1(Math) + {\rm ID}:2(Math) + {\rm ID}:3(Math) + {\rm ID}:4(Math) + {\rm ID}:5(Math) + {\rm ID}:6(Math) + {\rm ID}:7(Math)
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
est. Essayez de remplacer le score par une variable au lieu d'un nombre. Le score pour une personne avec ID: 1 sera $ x_1 $. Le nombre en bas à droite représente l'ID. Ensuite, la formule du score total est
Score total= {\rm ID}:1(Math) + {\rm ID}:2(Math) + {\rm ID}:3(Math) + {\rm ID}:4(Math) + {\rm ID}:5(Math) + {\rm ID}:6(Math) + {\rm ID}:7(Math)
\\
= x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
Est exprimé comme. Jusqu'à présent, il y avait 7 données, donc j'aurais dû régulièrement organiser les ajouts comme décrit ci-dessus, mais quand il y a 1000 données, ce n'est pas très bon, mais je ne peux pas l'écrire.
C'est là que $ \ sum $ est utile!
Points totaux= {\rm ID}:1(Math) + {\rm ID}:2(Math) + {\rm ID}:3(Math) + {\rm ID}:4(Math) + {\rm ID}:5(Math) + {\rm ID}:6(Math) + {\rm ID}:7(Math)
\\
= x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
\\
= \sum_{i=1}^7 x_i
\\
= 96 + 63 + 85 + 66 + 91 + 89 + 77 = 567
Il est exprimé comme. En d'autres termes

Alors
\sum_{i=1}^7 x_i = x_1 + x_2 + x_3 + x_4 + x_5 + x_6 + x_7
Sera. De cette façon même lorsqu'il y a 1000 données
\sum_{i=1}^{1000} x_i = x_1 + x_2 + \cdots + x_{1000}
Il est utilisé car il est pratique car il peut être exprimé sous la forme.
En premier lieu, si le nombre est décidé à l'avance, il n'est pas impossible d'écrire 1000 pièces d'affilée, mais le nombre de données n'est pas connu à ce moment, et même lorsqu'elles sont temporairement placées en $ n $ pièces pour le moment ,
\sum_{i=1}^{n} x_i
Vous pouvez écrire même si vous n'avez pas décidé! Pratique!
En passant, si vous savez comment l'exprimer dans le code, vous pourrez peut-être le comprendre immédiatement en disant qu'il s'agit du processus suivant. Le symbole $ \ sum $ est un processus de rotation et d'ajout avec une instruction for.
sum.py
x = [96, 63, 85, 66, 91, 89, 77]
total = 0
for i in range(len(x)):
total += x[i]
print total
</ i> 1. Quoi qu'il en soit, tout d'abord, moyenne
Pensons à nouveau à la "moyenne". Il existe différents types de moyennes, telles que la «moyenne arithmétique», la «moyenne géométrique» et la «moyenne harmonique», mais la soi-disant «moyenne» familière est la «moyenne arithmétique».
Ce sont toutes les données additionnées et divisées par ce nombre. En statistique, cette «moyenne» est exprimée par $ \ bar {x} $, et la définition est la suivante. Le nombre de données est de $ n $. Dans l'exemple du test de mathématiques de la section précédente, c'est $ n = 7 $ car ce sont les données de 7 étudiants.
\bar{x} = {1 \over n} \sum_{i=1}^{n} x_i
(Si vous ne comprenez pas la signification du symbole, veuillez consulter la [section précédente](http://qiita.com/kenmatsu4/items/e6c6acb289c02609e619#0 symbole))
Le graphique est le suivant. C'est intuitif: blush:
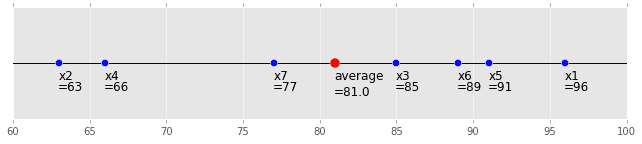 (code is here)
(code is here)
</ i> 2. Qu'est-ce que "déviation"?
Ensuite, j'expliquerai le concept de «déviation». Comme vous pouvez le voir, "l'écart type ** **" est un peu plus proche du noyau.
L'écart est la différence entre chaque donnée et la moyenne comme indiqué ci-dessous.
| ID | But | déviation |
|---|---|---|
| 1 | 96 | 96-81= 15 |
| 2 | 63 | 63-81= -18 |
| 3 | 85 | 85-81= 4 |
| 4 | 66 | 66-81= -15 |
| 5 | 91 | 91-81= 10 |
| 6 | 89 | 89-81= 8 |
| 7 | 77 | 77-81= -4 |
Ceci est également représenté par un graphique. La ligne rouge est l'écart de chaque donnée.
<! - La valeur standard de cet écart est "l'écart type". ->
 (code is here)
(code is here)
</ i> 3. Écart moyen
Avant de passer à l'écart type, j'aimerais vous présenter un «écart moyen» facile à comprendre intuitivement.
Il s'agit de la moyenne des «écarts» expliqués dans la section précédente. En d'autres termes
| ID | déviation |
|---|---|
| 1 | 15 |
| 2 | -18 |
| 3 | 4 |
| 4 | -15 |
| 5 | 10 |
| 6 | 8 |
| 7 | -4 |
Je pense à la moyenne de, mais il n'y a qu'un seul problème, et si vous les ajoutez tous, ce sera 0.
Ce que je veux faire
 Puisqu'il s'agit de la longueur moyenne de la ligne rouge de, le moins est omis.
Puisqu'il s'agit de la longueur moyenne de la ligne rouge de, le moins est omis.
En d'autres termes, la partie moins de cette longueur ...
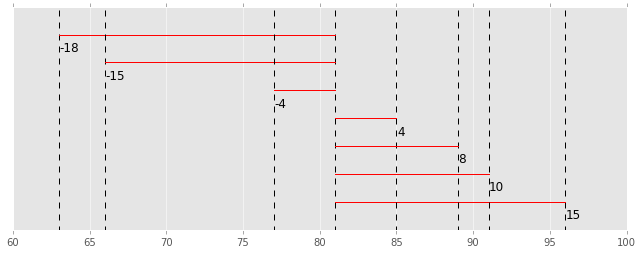 Inverser.
Inverser.

| ID | Valeur absolue de l'écart |
|---|---|
| 1 | 15 |
| 2 | 18 |
| 3 | 4 |
| 4 | 15 |
| 5 | 10 |
| 6 | 8 |
| 7 | 4 |
La valeur moyenne de cette «valeur absolue de l'écart» est ** 10,57 **, et cette valeur est appelée «écart moyen». c'est,
- Distance moyenne par rapport à la moyenne
- Indicateur de distance par rapport à la moyenne
C'est considéré. Dans cet exemple, le score moyen est de 81 points, mais le score moyen est de 10,57 points. Il n'est pas exagéré de dire que ce concept est presque l'idée d'un écart type. L'approche de calcul est légèrement différente. Donc, quand vous dites «écart type», j'aimerais que vous ayez l'image de «la moyenne de votre distance par rapport à la moyenne».
Exprimez-le en utilisant une formule.
Tout d'abord, le symbole de la valeur absolue
Lorsqu'il est écrit dans un graphique, il est exprimé comme ceci, et la pente est inversée de sorte que la valeur devient positive dans la zone où $ x $ est négatif.
 (code is here)
(code is here)
Exprimé dans une formule mathématique, cela ressemble à ceci.

On peut interpréter que l'écart est créé en soustrayant la moyenne de la valeur des données, le moins est supprimé en prenant la valeur absolue et la moyenne est prise.
Cela ressemble à ceci dans le code Python.
mean_deviation.py
x = [96, 63, 85, 66, 91, 89, 77]
ave = np.average(x)
total = 0
for i in range(len(x)):
total += abs(x[i] - ave)
print total/len(x)
</ i> 4. Écart type
Enfin, le personnage principal de cet article, «Écart type». Dans «l'écart moyen», la valeur absolue a été utilisée pour changer le moins en plus, mais dans «l'écart type», la méthode a été changée en carré et prendre le moins. En d'autres termes, l'idée est exactement la même, seule la méthode de suppression négative est différente.
Comme indiqué ci-dessous, il existe une similitude en ce que l'origine est le point de pliage et il est symétrique, et la valeur négative est changée en positive.

(code is here)
(La ligne bleue est la fonction de valeur absolue
Dans la section précédente, comme le montre la figure ci-dessous, la différence par rapport à la valeur moyenne était exprimée par la longueur de la ligne.

Cette fois, l'image de l'évaluation de la différence par le carré consiste à évaluer le degré d'écart par rapport à la valeur moyenne avec l'aire du carré comme indiqué ici.

Additionnons ces domaines et prenons la moyenne.

Exprimant cela comme une formule,

La somme des carrés des écarts par rapport à la moyenne et à la moyenne est appelée «dispersion». À ce stade, «l'écart type» n'est plus qu'à un pas.
La formule indiquée au début de cet article est réimprimée comme suit.
\sigma = \sqrt{ {1 \over n} \sum_{i=1}^n(x_i - \bar{x})^2}
La différence avec «distribué» est de savoir s'il faut ou non calculer l'itinéraire. La «distribution» est également un indicateur de la quantité de données dispersées, mais l'unité a changé car elle est considérée en termes de superficie. Vous pouvez donc ramener la zone à sa longueur en prenant la racine $ \ sqrt {\ } $.
En définissant que la racine $ \ sqrt {\ } $ est la valeur au carré, $ \ sqrt {9} = \ sqrt {3 ^ 2} = 3 $ ou $ \ sqrt {25} = \ sqrt Représente la relation {5 ^ 2} = 5 $. C'est le calcul inverse de 3 $ ^ 2 = 9 $. Puisque $ 25 $ peut être considéré comme l'aire d'un carré de 5 $ \ times5 $,

Ce sera comme ça une fois écrit dans une formule mathématique. Calculez la racine $ \ sqrt {\ } $ pour toute la distribution. Vous pouvez le considérer comme une "opération pour extraire la longueur du côté" par rapport à la valeur moyenne de la zone ci-dessus.
Autrement dit, l'écart type est
écart-type= \sqrt{Distribué}
Il devient.
Cela ressemble à ceci dans le code Python.
standard_deviation.py
x = [96, 63, 85, 66, 91, 89, 77]
ave = np.average(x)
total = 0
for i in range(len(x)):
total += (x[i] - ave)**2
print np.sqrt(total/len(x))
Aussi, la raison pour laquelle je l'ai changé en "carré" au lieu de "valeur absolue" est un peu difficile, mais comme le traitement de la valeur absolue utilisée pour l'écart moyen est mathématiquement difficile à gérer, j'ai adopté un carré facile à gérer. Un point est que cela a été fait. Après cela, en tant que concept de distance, il est plutôt naturel d'emprunter une route en quadrillant à partir du Théorème des trois carrés. Je pense que c'est aussi l'une des raisons.
Résumé
- La manipulation mathématique devient pratique
- Parce que le concept de distance peut être défini comme carré et acheminé en premier lieu
Je pense. (Une explication un peu plus détaillée sera donnée dans un autre article: grin :)
</ i> 5. Exemple 1: Comprendre avec un graphique
Comme je l'ai posté au début, j'écrirai un exemple dans un graphique. La moyenne de ces données est représentée par un cercle rouge, l'écart par rapport à la moyenne de chaque donnée est calculé et l'écart type est ensuite calculé à partir de celui-ci et exprimé par la longueur de la barre rouge.
C'est une image que la moyenne de la distance à la valeur moyenne de toutes les données est la longueur de cette barre rouge. Puisque nous faisons en sorte que les données soient générées sur une plage plus large, la longueur de la tige d'écart type augmentera également.
 (code is here)
(code is here)
</ i> 6. Exemple 2: valeur de l'écart
C'est une valeur d'écart familière pour les examens universitaires, etc., mais cette valeur d'écart est également basée sur «l'écart type».
Calculez l'écart moyen et standard à partir des données de toutes les personnes qui ont passé le test. Et
- Les personnes avec un score moyen ont une valeur d'écart de 50
- Valeur d'écart 60 pour ceux qui ont obtenu un écart type supérieur à la moyenne
- Valeur d'écart 40 pour ceux qui ont obtenu un écart type en dessous de la moyenne
Calculez comme suit. En d'autres termes
Valeur d'écart= { (But-moyenne) \sur l'écart type} \times 10 + 50
C'est une valeur calculée comme suit. Si le score est supérieur à la moyenne de la longueur de la barre rouge dans le graphique de la section précédente, la valeur de l'écart est de 60!
</ i> Enfin
Qu'as-tu pensé? J'ai essayé de l'expliquer le plus soigneusement possible, mais quand je l'ai réorganisé, je me suis rendu compte à nouveau que c'est un concept qui est composé d'une assez grande variété d'éléments entrelacés. Cependant, si je peux bien comprendre chaque élément, je pense que je peux avoir une intuition globale.
J'espère que la compréhension de cet écart type fera penser aux gens que «les statistiques sont intéressantes!» Et augmentera le nombre de personnes intéressées par l'analyse des données!
(* S'il y a une partie qui dit "Je ne sais pas", veuillez la laisser dans la section des commentaires!)
J'ai également écrit un article (diapositive) intitulé "Bases des statistiques", veuillez donc vous référer à cet article comme un article connexe si vous le souhaitez. http://qiita.com/kenmatsu4/items/5a59a7375140f29b31c2
Recommended Posts