Python-Dessine une courbe avec une distance Maharanobis égale à partir de deux jeux de données

La source

MahalanobisDistance.py

import numpy as np
import matplotlib.pyplot as plt
from sympy import *

CENTER1 = np.array([2.0, 3.0])
CENTER2 = np.array([-4.0, -1.0])

def calc_sum_of_square(data_list1, data_list2):
    return (len(data_list1) * sum([data1 * data2 for data1, data2 in zip(data_list1, data_list2)]) - sum(data_list1) * sum(data_list2))/(len(data_list1)*(len(data_list1)-1))

#Calcul matriciel distribué co-distribué
def calc_variance_covariance_matrix(data_list):
    return [[calc_sum_of_square(data_list1, data_list2)/(len(data_list1)-1) for data_list1 in data_list]
            for data_list2 in data_list]

def calc_average(data):
    return sum(data) / len(data)
            
if __name__ == "__main__":
    #Génère 50 points aléatoires centrés sur CENTRE1
    data_set1 = CENTER1 + 3.0 * np.random.rand(50, 2)
    #Génère 50 points aléatoires centrés sur CENTRE2
    data_set2 = CENTER2 + 4.7 * np.random.rand(50, 2)
    
    X1 = []
    Y1 = []
    X2 = []
    Y2 = []
    for data1, data2 in zip(data_set1, data_set2):
        X1.append(data1[0])
        Y1.append(data1[1])
        X2.append(data2[0])
        Y2.append(data2[1])
    
    # data_Calculer les variances et les covariances x et y de set1
    vc1 = np.array(calc_variance_covariance_matrix([X1, Y1]))
    # data_Calculer la co-distribution des distributions x et y de set2
    vc2 = np.array(calc_variance_covariance_matrix([X2, Y2]))
    det1 = vc1[0][0]*vc1[1][1] - vc1[0][1]**2
    det2 = vc2[0][0]*vc2[1][1] - vc2[0][1]**2
    x1_ave = calc_average(X1)
    y1_ave = calc_average(Y1)
    x2_ave = calc_average(X2)
    y2_ave = calc_average(Y2)
    
    # data_Maharanobis distance de set1: D1^2 = a11*x^2 + a22*y^2 + a12 * x * y + a1 * x + a2 * y + a0
    a11 = vc1[1][1]/det1
    a22 = vc1[0][0]/det1
    a12 = -2*vc1[0][1]/det1
    a1 = 2*(vc1[0][1]*y1_ave - vc1[1][1]*x1_ave)/det1
    a2 = 2*(vc1[0][1]*x1_ave - vc1[0][0]*y1_ave)/det1
    a0 = (vc1[1][1]*x1_ave**2 + vc1[0][0]*y1_ave**2 - 2*vc1[0][0]*x1_ave*y1_ave)/det1
    
    # data_Distance Maharanobis de set2: D1^2 = b11*x^2 + b22*y^2 + b12 * x * y + b1 * x + b2 * y + b0
    b11 = vc2[1][1]/det2
    b22 = vc2[0][0]/det2
    b12 = -2*vc2[0][1]/det2
    b1 = 2*(vc2[0][1]*y2_ave - vc2[1][1]*x2_ave)/det2
    b2 = 2*(vc2[0][1]*x2_ave - vc2[0][0]*y2_ave)/det2
    b0 = (vc2[1][1]*x2_ave**2 + vc2[0][0]*y2_ave**2 - 2*vc2[0][0]*x2_ave*y2_ave)/det2
    
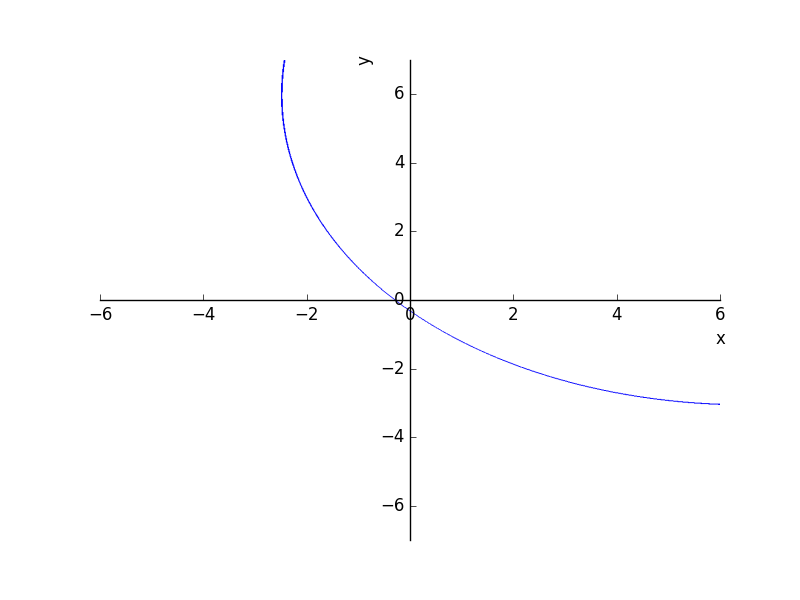
    # data_set1 et data_Tracez une courbe où les distances de set2 sont égales
    x, y = symbols("x y")
    f = (a11 - b11) * x**2 + (a22 - b22) * y**2 + (a12 - b12) * x * y + (a1 - b1) * x + (a2 - b2) * y + a0 - b0
    plot_implicit(f, (x, -6, 6), (y, -7, 7))   
    
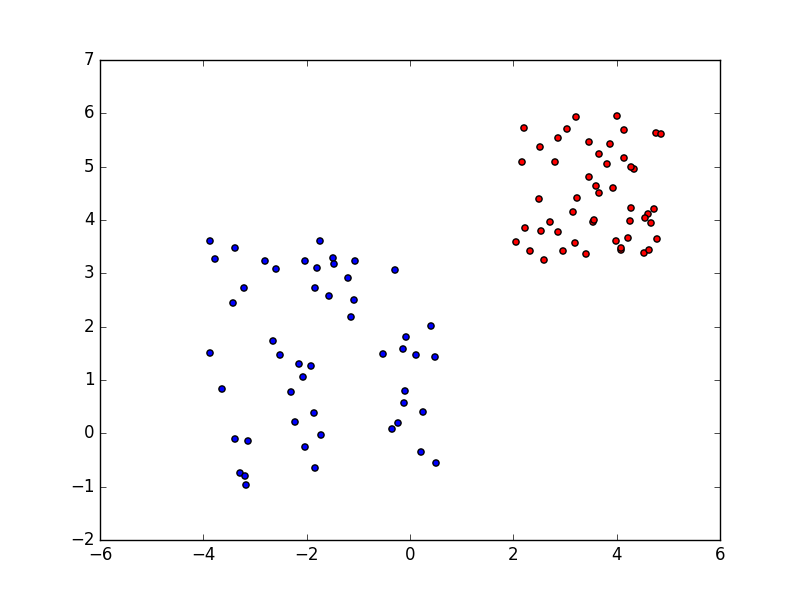
    # data_set1 et data_Dessinez un diagramme de dispersion de set2
    fig = plt.figure()
    ax = fig.add_subplot(1,1,1)
    ax.scatter(X1, Y1, c='red')
    ax.scatter(X2, Y2, c='blue')
    
    plt.show()

résultat