[PYTHON] Trouvez l'ordre de cuisson optimal

thème

Résolvons le problème de planification par le professeur Uno de l'Institut national d'informatique.

Réaliser au plus vite de nombreux procédés (soupe, poulet grillé, ...) en utilisant diverses ressources (personnes, cuisinière, couteau de cuisine, four).

Il peut être formulé et résolu avec un solveur à usage général, mais c'est difficile, alors utilisez le solveur de planification uniquement OptSeq. Il y a des frais, mais vous pouvez résoudre jusqu'à la variable 15 avec la version d'essai gratuite.

Voir Planifier le solveur d'optimisation OptSeq II pour l'installation et l'utilisation.

Résoudre avec Python

Définissez une fonction auxiliaire pour ne pas avoir à spécifier le nom un par un.

python

from more_itertools import pairwise
from optseq import *

def addResource(m, capacity=1, name=None, addResource_count=[0]):
    if name is None:
        addResource_count[0] += 1
        name = f'R{addResource_count[0]}'
    return m.addResource(name, capacity=capacity)
def addMode(dur, res=[], name=None, addMode_count=[0]):
    if name is None:
        addMode_count[0] += 1
        name = f'M{addMode_count[0]}'
    md = Mode(name, dur)
    for r in res:
        md.addResource(r, requirement=1)
    return md
def addActivity(m, dur, res=[], name=None, addActivity_count=[0]):
    if name is None:
        addActivity_count[0] += 1
        name = f'A{addActivity_count[0]}'
    ac = m.addActivity(name)
    md = addMode(dur, res)
    ac.addModes(md)
    return ac

Créons un modèle et résolvons-le. Les combinaisons des quatre ressources (personnes, cuisinière, cuisinette, four) sont réglées respectivement à 1, 2, 4, 8 afin qu'elles puissent être représentées par un chiffre. Le 5 dans "'soupe': [(5,10), ...]" signifie utiliser à la fois 1 (personne) et 4 (cuisine). 10 est le temps de travail (minutes).

python

# 1:Homme, 2:Conro, 4:Couteau de cuisine, 8:four
prm = {'soupe': [(5,10),(3,10),(0,20),(0,20)],
       'Yakitori': [(5,10),(9,20),(3,10)],
       'plats de poisson': [(3,10),(9,30)],
       'Légumes chauds': [(5,20),(3,10)],
       'thé': [(3,10)]} #Indicateur de ressource,temps
m = Model() #modèle
#Ressource
res = {i:addResource(m,j) for i,j in zip([1,2,4,8],[2,2,2,1])}
#Processus
act = {k:[addActivity(m, d, [r for j,r in res.items() if f&j], f'{k}{i+1}')
        for i,(f,d) in enumerate(l)] for k,l in prm.items()}
for l in act.values():
    for i,j in pairwise(l):
        m.addTemporal(i,j) #Dans l'ordre dans le même plat
m.addTemporal('sink',act['plats de poisson'][1],'CC') # plats de poisson2は最後に
m.addTemporal('sink',act['thé'][0],'CC') # thé1は最後に
m.Params.TimeLimit = 1 #Le temps de calcul peut aller jusqu'à 1 seconde
m.Params.Makespan = True #Minimisez l'heure de fin de tous les processus
m.optimize() #Exécution du solveur

résultat

 ================ Now solving the problem ================ 
Solutions:
    source     ---     0     0
      sink     ---    70    70
Soupe 1---     0    10
Soupe 2---    10    20
Soupe 3---    20    40
Soupe 4---    40    60
Yakitori 1---     0    10
Yakitori 2---    10    30
Yakitori 3---    30    40
Plat de poisson 1---    20    30
Plat de poisson 2---    40    70
Légumes chauds 1---    30    50
Légumes chauds 2---    50    60
Thé 1---    60    70

Les deux nombres représentent les heures de début et de fin du processus. Puisque l'évier est de 70, nous pouvons voir que l'ensemble du processus est terminé en 70 minutes. De plus, même si vous le regardez individuellement, vous pouvez voir que la réponse est presque la même que celle de l'enseignant ci-dessous.

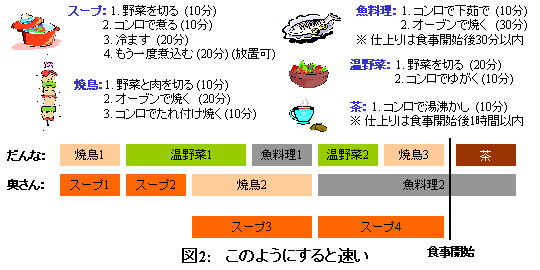
c'est tout