1. Statistiques apprises avec Python 2-1. Distribution de probabilité [variable discrète]
- ** Variable stochastique discrète ** est une variable qui prend des valeurs discrètes comme un dé, par exemple, "2" après "1", "3" après "2", etc. En attendant, il n'y a pas de nombres continus tels que 1,1, 1,2, 1,3, ..., 1,8, 1,9.
- Nous examinerons les caractéristiques des principales ** distributions de probabilité discrètes ** en utilisant
pmf(fonction de masse de probabilité) etrvs(variables aléatoires) de scipy.stats. Je vais.
#Import de la bibliothèque de calculs numériques
import numpy as np
import scipy as sp
import pandas as pd
from pandas import Series, DataFrame
#Importer la bibliothèque de visualisation
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
%matplotlib inline
#Module d'affichage japonais de matplotlib
!pip install japanize-matplotlib
import japanize_matplotlib
⑴ Distribution Bernoulli
- La survenue de l'un ou l'autre des deux seuls types d'événements est appelée le ** procès de Bernoulli **.
- ** Distribution de Bernoulli ** est la distribution de probabilité que chaque événement se produise dans un essai de Bernoulli.
- Par exemple, si vous lancez une pièce 8 fois et que le recto sort, ce sera 0, et si le verso sort, ce sera 1 et le résultat est supposé comme suit.
x = np.array([0,0,1,1,0,1,0,0])
#Calculer la distribution de probabilité
p = len(x[x==1]) / len(x)
pmf_bernoulli = sp.stats.bernoulli.pmf(x, p)
#Visualisation
plt.vlines(x, 0, pmf_bernoulli,
colors='blue', lw=50)
plt.xticks([0,1])
plt.xlim([0 - 0.5, 1 + 0.5])
plt.grid(True)
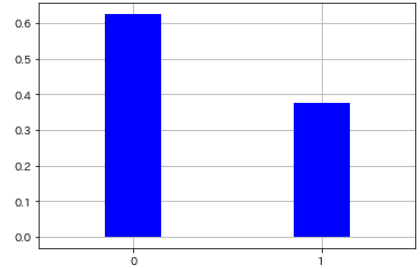
| Deux types d'événements | probabilité |
|---|---|
| 0 | 0.625 |
| 1 | 0.375 |
⑵ Distribution binomiale
- La distribution de probabilité du nombre de fois qu'un événement se produit lorsque les essais de Bernoulli qui sont indépendants les uns des autres sont répétés n fois est appelée ** distribution binomiale **.
- Par exemple, utilisez
binom.pmfpour trouver la probabilité qu'une pièce avec une probabilité p de 50% apparaisse 5 fois et 2 d'entre elles apparaissent.
sp.stats.binom.pmf(n=5, p=0.5, k=2)
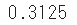
- En supposant que l'essai de lancer des pièces avec une probabilité p de 20% d'apparaître 10 fois et de compter le nombre de fois où le tableau apparaît a été répété 10000 fois, utilisez
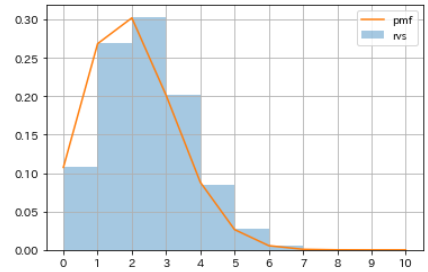
binom.rvspour générer un nombre pseudo aléatoire qui suit une distribution binomiale. Faire. - De plus, en utilisant
binom.pmf, calculez la distribution de probabilité du nombre de fois où le tableau apparaît lorsque vous lancez une pièce avec une probabilité p de 20% qui apparaît 10 fois, et comparez-la avec l'histogramme des nombres pseudo aléatoires.
#Générer un nombre pseudo aléatoire
np.random.seed(1)
rvs_binom = sp.stats.binom.rvs(n=10, p=0.2, size=10000)
#Obtenir une distribution de probabilité
m = np.arange(0, 10+1, 1)
pmf_binom = sp.stats.binom.pmf(n=10, p=0.2, k=m)
#Visualisation
sns.distplot(rvs_binom, bins=m,
kde=False, norm_hist=True, label='rvs')
plt.plot(m, pmf_binom, label='pmf')
plt.xticks(m)
plt.legend()
plt.grid()
| Nombre de fois où le tableau apparaît | probabilité |
|---|---|
| 0 | 0.107374182 |
| 1 | 0.268435456 |
| 2 | 0.301989888 |
| 3 | 0.201326592 |
| 4 | 0.088080384 |
| 5 | 0.026424115 |
| 6 | 0.005505024 |
| 7 | 0.000786432 |
| 8 | 0.000073728 |
| 9 | 0.000004096 |
| 10 | 0.000000102 |
⑶ Distribution de Poisson
- La probabilité d'un événement très rare, comme le nombre de gouttes de pluie par unité de surface ou le nombre d'accidents qui se produisent à une intersection dans une année, suit la ** distribution de Poisson **.
- En d'autres termes, il s'agit d'une distribution de probabilité qui se produit à un taux constant pendant un certain temps ou une certaine zone, et le nombre d'échantillons n est suffisamment grand et la probabilité p est très petite.
- Par exemple, utilisez
poisson.pmfpour trouver la probabilité qu'une moyenne de 5 occurrences se produise seulement 2 fois dans une période donnée.
sp.stats.poisson.pmf(k=2, mu=5)
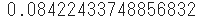
- Le paramètre de la distribution de Poisson est le ** nombre moyen d'occurrences mu ** d'un événement, également appelé ** intensité ** ou ** λ (lambda) **.
- En supposant que la probabilité p qu'un événement se produise est de 20% et que le nombre de fois qu'il s'est produit est répété 10000 fois,
poisson.rvsest utilisé pour générer un nombre pseudo-aléatoire qui suit la distribution de Poisson. - De plus, en utilisant
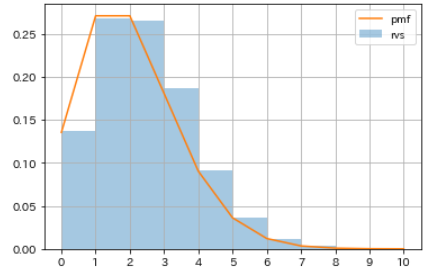
poisson.pmf, calculez la distribution de probabilité lorsque la probabilité d'occurrence p est de 20%, et comparez-la avec l'histogramme des nombres pseudo aléatoires.
#Générer un nombre pseudo aléatoire
np.random.seed(1)
rvs_poisson = sp.stats.poisson.rvs(mu=2, size=10000)
#Obtenir une distribution de probabilité
m = np.arange(0, 10+1, 1)
pmf_poisson = sp.stats.poisson.pmf(mu=2, k=m)
#Visualisation
sns.distplot(rvs_poisson, bins=m,
kde=False, norm_hist=True, label='rvs')
plt.plot(m, pmf_poisson, label='pmf')
plt.xticks(m)
plt.legend()
plt.grid()
| Nombre d'occurrences | probabilité |
|---|---|
| 0 | 0.135335283 |
| 1 | 0.270670566 |
| 2 | 0.270670566 |
| 3 | 0.180447044 |
| 4 | 0.090223522 |
| 5 | 0.036089409 |
| 6 | 0.012029803 |
| 7 | 0.003437087 |
| 8 | 0.000859272 |
| 9 | 0.000190949 |
| 10 | 0.000038190 |
- Considérons maintenant la relation entre la ** distribution de Poisson ** et la ** distribution binomiale **.
- Calculez la distribution de probabilité de la ** distribution binomiale ** lorsque le nombre d'essais n est suffisamment grand et la probabilité p est très petite, et comparez-la avec l'exemple précédent de la ** distribution de Poisson **.
#Spécifiez les paramètres
n = 100000000
p = 0.00000002
#Calculer la distribution de probabilité de la distribution binomiale
num = np.arange(0, 10+1, 1)
pmf_binom_2 = sp.stats.binom.pmf(n=n, p=p, k=num)
#Visualisation
plt.plot(m, pmf_poisson,
color='lightgray', lw=10, label='poisson')
plt.plot(m, pmf_binom_2,
color='black', linestyle='dotted', label='binomial')
plt.xticks(num)
plt.legend()
plt.grid()
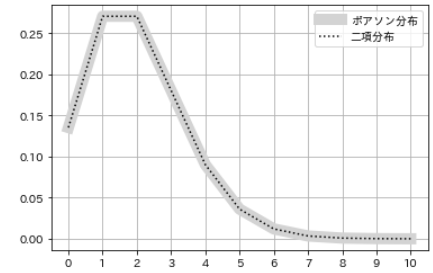
- Dans ce cas, la ** distribution de Poisson ** et la ** distribution binomiale ** sont presque les mêmes, ce qui indique qu'elles sont étroitement liées.
- ** Distribution de Poisson ** se rapproche de la situation où la probabilité p de ** distribution binomiale ** est très faible et le nombre d'essais n est suffisamment grand.
⑷ Distribution géométrique
- Lors de la répétition d'essais de Bernoulli indépendants avec une probabilité de succès de p, la distribution de probabilité ** suivie du nombre d'essais k jusqu'au premier succès est appelée ** distribution géométrique **.
- Par exemple, utilisez
geom.pmfdans scipy.stats pour obtenir la probabilité de lancer un dé une seule fois et d'obtenir un" 1 ".
%precision 3
sp.stats.geom.pmf(k=1, p=1/6)
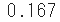
- Il y a 6 dés en tout, et si tous ont la même probabilité, il est naturel que 1/6 soit 0,167,
- Lancez-les l'un après l'autre et trouvez la probabilité que "1" apparaisse pour la première fois la deuxième fois, la probabilité que "1" apparaisse pour la première fois la troisième fois, ..., et la probabilité que "1" apparaisse pour la première fois dans la dixième fois.
#Spécifiez le nombre d'essais
num = np.arange(1, 11, 1)
#Calculer la distribution de probabilité
prob = []
for i in num:
value = sp.stats.geom.pmf(k=i, p=1/6)
prob.append(value)
#Visualisation
plt.bar(num, prob)
plt.xticks(num)
plt.xlabel('Nombre de fois jusqu'à ce que 1 apparaisse pour la première fois')
plt.ylabel('probabilité')
plt.show()
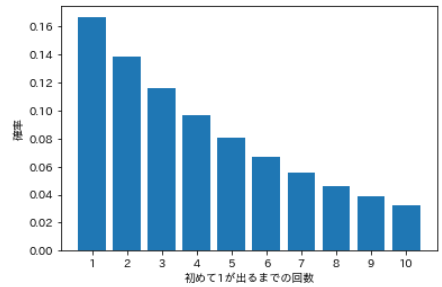
- La probabilité de lancer k fois, d'échouer jusqu'à la k-1ème fois et de réussir pour la première fois à la kème fois, la distribution de probabilité dans ce cas est la suivante.
| Nombre d'essais | probabilité | une formule |
|---|---|---|
| 1 | 0.167 | ⅙ |
| 2 | 0.139 | ⅚ ・ ⅙ |
| 3 | 0.116 | ⅚ ・ ⅚ ・ ⅙ |
| 4 | 0.096 | ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
| 5 | 0.080 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
| 6 | 0.067 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
| 7 | 0.056 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
| 8 | 0.047 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
| 9 | 0.039 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
| 10 | 0.032 | ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅚ ・ ⅙ |
⑸ Distribution uniforme
- Il existe deux types de distribution uniforme, de type discret et de type continu. La distribution uniforme avec des variables de probabilité discrètes est appelée ** distribution uniforme discrète **.
- Une distribution avec des probabilités égales de tous les événements, par exemple les dés suivent ** distribution uniforme discrète ** parce que tous les dés ont des probabilités égales de lancer de 1 à 6.
#Spécifiez tous les événements
num = np.arange(1, 7, 1)
#Calculer la distribution de probabilité
prob = []
for i in num:
value = 1 / len(num)
prob.append(value)
#Visualisation
plt.bar(num, prob)
plt.xticks(num)
plt.xlabel('Yeux de dés')
plt.ylabel('probabilité')
plt.show()
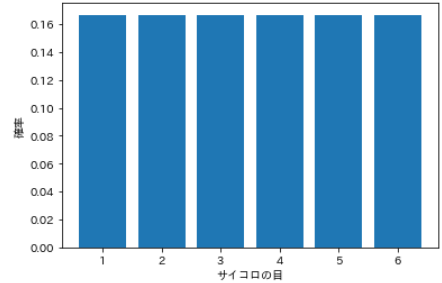
| Yeux de dés | probabilité |
|---|---|
| 1 | 0.167 |
| 2 | 0.167 |
| 3 | 0.167 |
| 4 | 0.167 |
| 5 | 0.167 |
| 6 | 0.167 |
⑹ distribution hypergéométrique
- Par exemple, supposons que vous ayez un total de 20 loteries, dont 7 sont gagnantes. Combien de coups obtiendrez-vous en sélectionnant au hasard 12 sur 20?
- La distribution qui utilise ce «nombre à attribuer» comme variable stochastique est appelée ** distribution supergéométrique **.
- Il y a trois paramètres, qui sont le nombre total M, le nombre n par et le nombre N à sélectionner.
#Spécifiez les paramètres
M = 20 #Nombre total
n = 7 #Nombre de visites
N = 12 #Nombre de sélections
#Créer une variable stochastique
k = np.arange(0, n+1)
#Créer un modèle
hgeom = sp.stats.hypergeom(M, n, N)
#Calculer la distribution de probabilité
pmf_hgeom = hgeom.pmf(k)
#Visualisation
plt.bar(k, pmf_hgeom)
plt.xticks(k)
plt.xlabel('Nombre de visites')
plt.ylabel('probabilité')
plt.show()
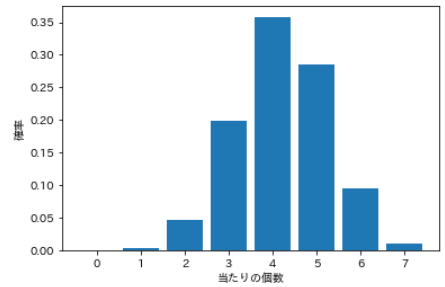
| Nombre de visites | probabilité |
|---|---|
| 0 | 0.00010 |
| 1 | 0.00433 |
| 2 | 0.04768 |
| 3 | 0.19866 |
| 4 | 0.35759 |
| 5 | 0.28607 |
| 6 | 0.09536 |
| 7 | 0.01022 |
⑺ Distribution binomiale négative
- ** Distribution binomiale négative ** trouve la probabilité de succès k fois dans n essais, à condition que le dernier essai soit réussi.
- Dans la distribution binomiale, le nombre de succès k est une variable stochastique, mais dans la ** distribution binomiale négative **, le nombre de succès k est fixe. ** Pour la variable de probabilité, utilisez le nombre d'échecs n-k ** au lieu du nombre d'essais n.
- Par exemple, combien de fois devez-vous lancer un tirage au sort à plusieurs reprises avant qu'il ne sorte trois fois? En d'autres termes, le nombre d'échecs, c'est-à-dire le nombre de fois où il doit échouer avant de réussir trois fois, est une variable stochastique.
#Spécifiez les paramètres
N = 12 #Nombre d'essais
p = 0.5 #Probabilité de succès
k = 3 #Nombre de succès
#Calculer la distribution de probabilité
pmf_nbinom = sp.stats.nbinom.pmf(range(N), k, p)
#Visualisation
plt.bar(range(N), pmf_nbinom)
plt.xlabel('Nombre de pannes')
plt.ylabel('probabilité')
plt.xticks(range(N))
plt.show()
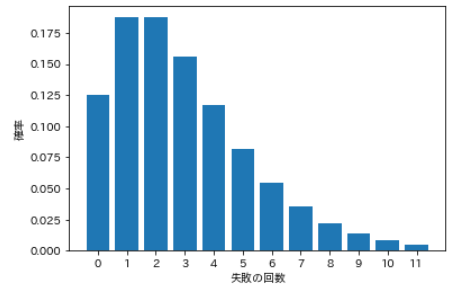
| Nombre de pannes | probabilité |
|---|---|
| 0 | 0.125 |
| 1 | 0.188 |
| 2 | 0.188 |
| 3 | 0.156 |
| 4 | 0.117 |
| 5 | 0.082 |
| 6 | 0.055 |
| 7 | 0.035 |
| 8 | 0.022 |
| 9 | 0.013 |
| 10 | 0.008 |
| 11 | 0.005 |
Sommaire
Nous avons examiné la distribution de probabilité discrète, mais nous la résumerons dans une liste avec une conscience de ce que sera la variable de probabilité et, en un mot, ce qu'il faut mettre sur l'axe des x.
| Types de distribution de probabilité | Variable probabiliste | Paramètres | |
|---|---|---|---|
| ⑴ | Distribution de Bernoulli | Événement 0, 1 | Probabilité d'occurrence p |
| ⑵ | Distribution binaire | Nombre d'essais | Probabilité d'occurrence p,Nombre d'occurrences k,Nombre d'essais n |
| ⑶ | Distribution de Poisson | Nombre d'essais | Nombre moyen d'occurrences mu |
| ⑷ | Distribution géométrique | Nombre d'essais | Probabilité de succès p,Nombre d'essais k |
| ⑸ | Distribution uniforme discrète | Type d'événement | ※scipy.La distribution uniforme des atats est de type continu uniquement |
| ⑹ | Distribution super géométrique | Nombre de succès | Nombre total M,Nombre de succès dans l'ensemble n,Nombre de sélections N |
| ⑺ | Distribution binomiale négative | Nombre de pannes | Probabilité de succès p,Nombre de succès k,Nombre d'essais N |
Recommended Posts