Le traitement de l'image est difficile. En regardant les magnifiques filtres d'Instagram, la Photo Sphere de Google et ces services, les images semblent intéressantes! Un livre de traitement d'image qui s'est ouvert avec enthousiasme. Nous n'avions pas d'autre choix que de pétrifier les formules mathématiques énumérées ici, mais que reste-t-il d'autre à la voix chuchotée à nos oreilles, "OpenCV fera les choses difficiles, non?" J'aurais pu le faire.

J'espère que cet article montrera la voie (en termes d'objets, d'aiguilles en or) à ceux qui veulent surmonter ces jours où ils ont dû pétrifier et comprendre la théorie de base tout en utilisant OpenCV. pense. Le champ d'application couvert est la «vision par ordinateur pratique» (https://www.oreilly.co.jp/books/9784873116075/), qui est à la base de tout traitement. Équivalent). De plus, puisque cet article lui-même est écrit tout en étant compris par moi en tant que débutant, j'apprécierais que les aventuriers avancés du traitement d'image puissent signaler des erreurs.

Quels sont les points caractéristiques de l'image?

Pourquoi les humains peuvent-ils assembler des puzzles? En y réfléchissant, nous pouvons y penser comme saisir les caractéristiques de chaque pièce du puzzle, trouver des caractéristiques similaires et continues et les relier. De même, vous pouvez combiner plusieurs photos en une photo panoramique, car vous trouvez et connectez des fonctionnalités communes entre les photos.

CS231M Mobile Computer Vision Class,Lecture5, Stitching + Blending, p4~

Si vous pensez à ces «points caractéristiques» de plus en plus simplement, vous pouvez enfin les résumer dans les trois suivants.

bord: Il y a une limite où la différence peut être reconnue
coin: le point où les arêtes sont concentrées
plat: ni bord ni coin, le point qu'aucune caractéristique ne peut être reconnue

Et, compte tenu de la composition des photos panoramiques comme décrit ci-dessus, il est nécessaire de suivre les règles suivantes lors de la recherche de ce "point caractéristique".

Reproductibilité: un point caractéristique est toujours reconnu comme un point caractéristique
Distinguishabilité: un point caractéristique peut être identifié comme distinctement différent des autres points caractéristiques

En ce qui concerne la reproductibilité, par exemple, si les points caractéristiques qui sont reconnus lorsque l’angle auquel la photo est prise change radicalement, le processus de connexion des points caractéristiques sera interrompu.

Par conséquent, il est préférable de pouvoir reconnaître des points caractéristiques robustes ** qui ne changent pas avec l'angle ou le grossissement de l'image.

En ce qui concerne le caractère distinctif, si les points caractéristiques reconnus ne peuvent pas être identifiés de manière unique, il sera difficile de savoir lequel correspondre.

Par conséquent, il est important de disposer d'une méthode de représentation qui permette à chaque point caractéristique d'être identifié de manière unique.

C'est exactement ce qui est requis pour la détection des fonctionnalités et la description des fonctionnalités. En d'autres termes, détecter «un point caractéristique robuste qui ne change pas avec l'angle ou le grossissement de l'image» (détection de caractéristique) et l'exprimer avec une «méthode d'expression identifiable de manière unique» autant que possible (description de caractéristique) dans l'image. C'est l'objectif de reconnaître les points caractéristiques.

Maintenant, regardons la détection des points caractéristiques et la méthode d'expression des points caractéristiques dans l'ordre.

Détection des fonctionnalités

La procédure de détection des points caractéristiques consiste généralement à «détecter le bord», puis à «détecter le coin» où les bords sont concentrés.

détection de bord

Plus précisément, le bord est le "point où la luminosité change de manière significative". À titre d'exemple simple, considérons l'image d'un carreau noir avec un cercle blanc. Si vous tracez la luminosité sur la ligne rouge tirée du côté comme indiqué ci-dessous le long des axes de coordonnées, vous devriez obtenir un graphique dans lequel la luminosité saute dans le cercle blanc au milieu.

Ici, ce que nous voulons détecter est le bord, c'est-à-dire le point sur le graphique qui change considérablement de sombre-> clair, clair-> sombre. Afin de connaître le degré de changement à un certain point, calculons le taux de changement à partir des valeurs des points avant et après ce point.

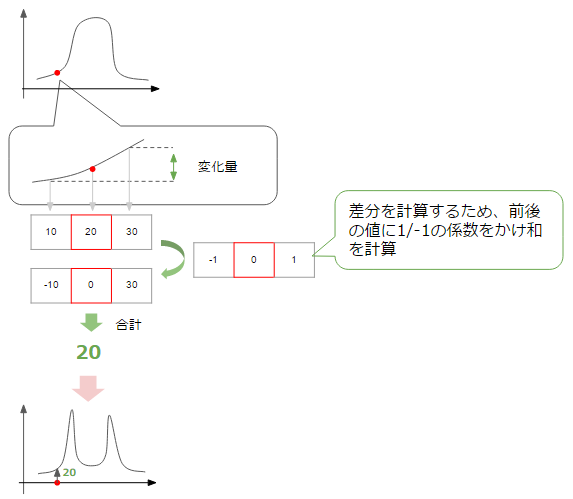
Ensuite, comme le montre la figure ci-dessus, vous pouvez obtenir un graphique dans lequel le taux de changement augmente au point où le changement est important, c'est-à-dire la partie correspondant au bord (le montant du changement a + -, mais ici la valeur absolue est tracée. Veuillez réfléchir). À l'heure actuelle, nous considérons la quantité de changement dans la direction horizontale de la figure, mais la même chose peut être considérée dans la direction verticale.

En fin de compte, il semble que l'arête puisse être détectée en additionnant la quantité de changement dans les directions horizontale et verticale (généralement la somme des racines carrées) et en collectant des points dont la valeur est supérieure à un certain seuil (seuil).

C'est l'idée de base de la détection de bord, et bien que la détection de bord soit possible avec cela seul, il existe certaines techniques pour une détection plus précise, alors jetons un coup d'œil.

Lissage

Il s'agit d'une méthode qui prend également en compte la partie périphérique lors du calcul du montant de la monnaie. En gros, c'est comme prendre une moyenne. En calculant la moyenne, le changement de valeur peut être lissé (lissage) et, par conséquent, des bords connectés en douceur peuvent être détectés.

La figure ci-dessous montre comment la quantité de changement dans la direction horizontale est calculée en tenant compte de la quantité de changement aux points adjacents. Le lissage est obtenu en additionnant un total de trois changements.

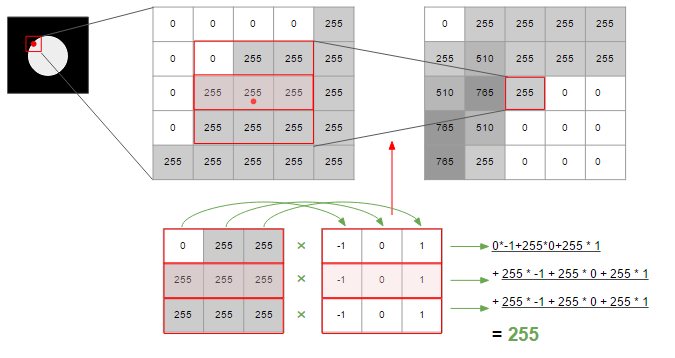
Dans la figure ci-dessus, afin de calculer le montant du changement, il est calculé à l'aide d'une matrice contenant la valeur de -1/0/1 de 3 * 3. La matrice et le traitement pour calculer ces changements sont appelés ** filtres **.

Il existe différents types de ce filtre, et celui utilisé dans la figure ci-dessus est le filtre Prewitt. Le filtre Sobel est plus axé sur ce qui est adjacent au centre que Prewitt, et Gaussian peut utiliser une fonction de distribution normale, avec le centre comme sommet et multipliant doucement le coefficient vers le bord. La méthode Canny, qui est souvent utilisée pour détecter les arêtes, est une méthode qui utilise ce filtre gaussien.

Notez qu'il est nécessaire d'effectuer une interpolation pour le bord de l'image car il n'y a pas de points adjacents. Il existe les méthodes suivantes pour cette méthode d'interpolation.

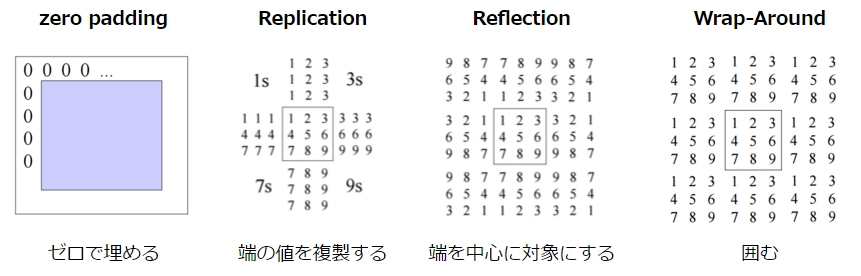CSE/EE486 Computer Vision I, Lecture3, p26~

C'est tout pour la détection des bords. Je vais résumer le contenu jusqu'à présent.

Pour détecter le bord, utilisez la quantité de changement de luminosité de l'image comme indice.
La quantité de changement peut être prise dans deux directions, la direction horizontale et la direction verticale. La somme des racines carrées de cette valeur est utilisée comme quantité de changement, et c'est ce qu'on appelle la magnitude.
Le bord peut être détecté en déterminant le bord lorsque la magnitude dépasse un certain seuil.
Généralement, le lissage est effectué lors du calcul de la quantité de changement. Il s'agit d'améliorer la précision de détection en ajoutant la quantité de changement dans l'environnement.
Il existe différents types de filtres qui définissent la portée de cette «périphérie» et sa pondération.

Détection de coin

Vient ensuite la détection du coin. Ici, nous allons expliquer le détecteur de coin Harris, qui est souvent utilisé pour détecter les coins. C'est une méthode qui fait bon usage des caractéristiques de la matrice, et donne intuitivement une image proche de l'analyse en composantes principales.

Je laisserai l'explication détaillée de l'analyse en composantes principales à d'autres articles, mais les deux points suivants sont importants.

Trouvez un indicateur qui peut expliquer la direction dans laquelle les données se propagent. Cela correspond au vecteur propre de la matrice.
La valeur unique obtenue à la suite du calcul représente le pouvoir explicatif de l'indice.

En appliquant cela à Harris, les «données» sont, bien sûr, un résumé de la quantité de changement dans chacune des directions horizontale et verticale à un certain point. Ensuite, à partir de l'explication de l'analyse en composantes principales ci-dessus, elle peut être déduite comme suit.

Le vecteur propre représente la "direction dans laquelle la quantité de changement se propage", c'est-à-dire la direction du bord.
Lorsque la valeur propre est grande, cela signifie que "la capacité à expliquer la quantité de changement est élevée", c'est-à-dire la force du bord.

Cela permet de détecter d'abord les arêtes, et s'il y a "plusieurs vecteurs propres avec de grandes valeurs propres", cela signifie qu'il y a plusieurs arêtes, c'est-à-dire des coins. En supposant que les valeurs uniques sont respectivement $ \ lambda1 $ et $ \ lambda2 $, elles peuvent être classées comme suit en fonction de la taille des valeurs.

CSE/EE486 Computer Vision I, Lecture 06, Corner Detection, p19

J'expliquerai également la formule. Tout d'abord, un point $ I (x, y) $ sur l'image $ I $ et un point $ I (x + u, y + v) déplacés de $ u $ dans la direction $ x $ et de $ v $ dans la direction $ y $. Si le montant de la variation entre) $ est $ E (u, v) $, il peut être exprimé comme suit dans la formule.

E(u, v) = \sum_{x, y} w(x, y) [I(x+u, y+v) - I(x, y)]^2

$ w (x, y) $ est une fonction de fenêtre qui devient un filtre (gaussien). L'image est que le montant du changement est $ [I (x + u, y + v) --I (x, y)] ^ 2 $, et ceci est lissé avec $ w (x, y) $ pour calculer le montant du changement. est. L'approche de cette formule en utilisant l'expansion de Taylor est la suivante (la formule d'expansion est omise. Si vous êtes intéressé, veuillez vous référer au matériel de conférence lié ci-dessus).

E(u, v) \simeq [u, v] M \begin{bmatrix} u \\ v \end{bmatrix}

Où $ M $ est:

M = \sum_{x, y} w(x, y) \begin{bmatrix} I_X^2 & I_x I_y \\ I_x I_y & I_y ^2 \end{bmatrix}

$ I_x $ et $ I_y $ sont les différences sur l'axe des x et l'axe des y, respectivement, et lorsque $ [I_x, I_y] $ est au carré, la partie de matrice ci-dessus est obtenue. Ce que vous faites est la même chose que $ [I (x + u, y + v) --I (x, y)] ^ 2 $ dans la formule ci-dessus. Et c'est la "matrice qui décrit la quantité de changement", et en la décomposant en valeurs singulières, il est possible de juger le bord et le coin comme décrit au début.

Cependant, il est assez difficile de calculer la valeur propre, alors essayez de ne pas la calculer là où elle n'est pas nécessaire. Les indicateurs suivants sont utilisés à cet effet.

R = det M -k(trace M)^2

det M = \lambda1 \lambda2

trace M = \lambda1 + \lambda2

$ k $ est une constante d'environ 0,04 ~ 0,06. Il peut être classé comme suit en fonction de la valeur de R.

Grand R: coin
Petit R: plat
R < 0: edge

La figure est la suivante.

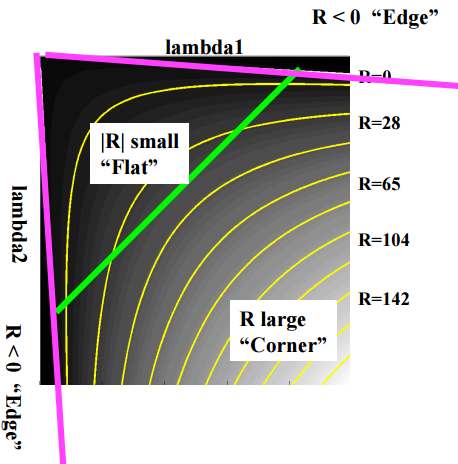CSE/EE486 Computer Vision I, Lecture 06, Corner Detection, p22

Vous pouvez maintenant détecter le coin rapidement. Voici un résumé de la détection de coin.

le coin peut être défini comme un endroit où plusieurs bords se rassemblent
La direction du bord peut être trouvée à partir du vecteur propre de la matrice qui résume la quantité de changement, et l'ampleur de la quantité de changement (ressemblance au bord) peut être trouvée à partir de l'amplitude de la valeur propre.
Le bord, le coin et le plat peuvent être déterminés en fonction des valeurs des deux valeurs uniques.
Puisqu'il est difficile de calculer la valeur propre, utilisez la formule de jugement pour simplifier le calcul.

Puisque Harris considère le vecteur propre qui est la direction du bord, il est robuste contre l'inclinaison de l'image. Cependant, il n'est pas robuste en termes d'échelle. En effet, les coins deviennent plus lâches à mesure que vous vous développez, ce qui rend plus difficile la distinction des bords.

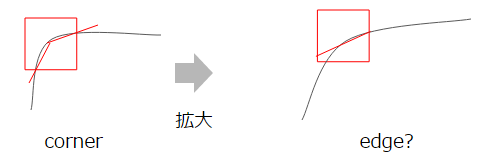
FAST est une méthode conçue pour surmonter cela. Je vais omettre les détails, mais c'est une méthode pour reconnaître une série de n points qui sont plus sombres ou plus clairs que le point central. Il s'agit littéralement d'une méthode FAST et robuste contre la rotation et l'expansion.

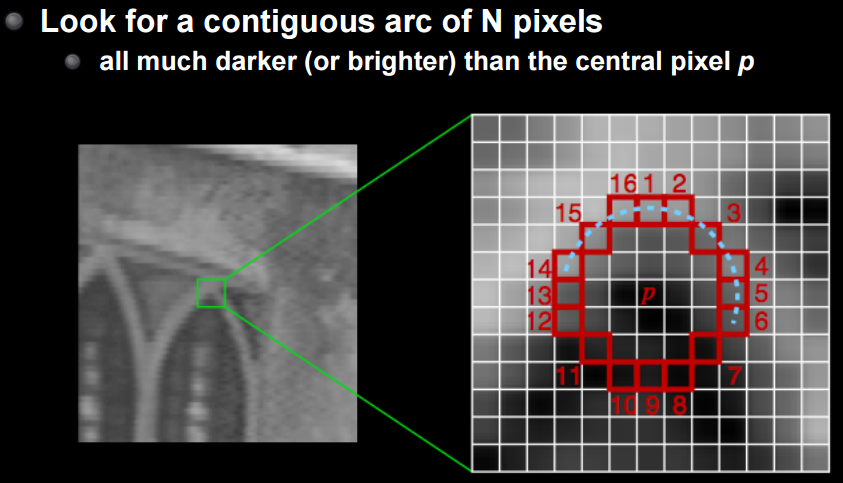CS231M Mobile Computer Vision Class,Lecture5, Stitching + Blending, p24

Description de fonctionnalité

Les points caractéristiques peuvent maintenant être détectés. La prochaine fois, j'aimerais pouvoir faire correspondre des images en créant une expression d'entité unique et une description d'entité à l'aide des points d'entité.

Comme je l'ai mentionné un peu, les trois caractéristiques suivantes sont souhaitables pour cette description de fonctionnalité.

Traduction: robuste pour les diapositives d'images
Rotation: robuste contre la rotation de l'image
Mise à l'échelle: robuste pour l'agrandissement / la réduction d'image

La traduction est relativement facile à gérer car elle ne fait que changer la position, et la rotation est assez bonne, comme mentionné dans Harris dans la section précédente. Cependant, il est difficile de prendre en charge la mise à l'échelle. Comme vous pouvez le voir sur la figure ci-dessous, les informations de l'image changent considérablement en fonction du grossissement.

CSE/EE486 Computer Vision I, Lecture 31, Object Recognition : SIFT Keys, p31

En premier lieu, si vous le développez, il est évident que les informations seront perdues si vous n'étendez pas la plage correspondante en conséquence. En effet, la zone qui correspond à la même plage change.

En d'autres termes, il est nécessaire de considérer l'échelle pour satisfaire les trois caractéristiques ci-dessus. Dans Harris, il n'y avait que la «direction» et la «force» du vecteur propre et de la valeur propre, mais ici il s'agit d'ajouter «l'échelle», c'est-à-dire quelle valeur d'agrandissement est obtenue. L'image ressemble à ce qui suit.

La méthode SIFT permet la détection et la description des points caractéristiques qui prennent en compte cette échelle.

SIFT (Scale Invariant Feature Transform)

Le cœur de SIFT est l'extraction des points caractéristiques pour chaque échelle. La méthode utilisée pour cela est LoG / DoG. Log est une abréviation de laplacien de gaussien, et le point avec le plus grand changement dans l'image lissée par le filtre gaussien est obtenu par double différenciation (= laplacien). Puisque le gaussien est tel que décrit dans Lissage, je vais expliquer brièvement pourquoi le point avec la quantité maximale de changement est obtenu par le différentiel du second ordre (= laplacien).

Pensez à la différenciation comme simplement à la recherche de la quantité de changement à un moment donné. Ensuite, vous pouvez voir ce qui suit.

Différenciation de premier ordre: Représente la quantité de changement par rapport à la fonction d'origine = Le sommet représente le point où la quantité de changement est maximale (minimum)
Différenciation de second ordre: un changement dans la direction du changement se produit près du sommet de la différenciation du premier ordre, qui représente le changement de la quantité de changement. Le sommet de la différenciation du premier ordre est égal au point de passage à zéro.

En d'autres termes, le point où $ I (x) '' = 0 $ est élevé comme le point avec la plus grande quantité de changement et le point caractéristique. Le filtre équivalent à l'application de cette différenciation quadratique est appelé "filtre raprasien", et plus la valeur est proche de 0, plus la possibilité de points caractéristiques est élevée.

Cependant, il n'est pas possible de distinguer entre 0 (= pas de changement) points et ceux au sommet au stade de la différenciation du premier ordre uniquement par la différenciation du second ordre, il est donc nécessaire de vérifier en même temps si la valeur de la différenciation du premier ordre est suffisamment grande. Comme vous pouvez le voir, il est très vulnérable au bruit.

Ensuite, revenant à LoG, comme son nom l'indique, il s'agit d'une méthode de lissage avec un filtre gaussien, puis de trouver le point avec le montant maximal de changement = point caractéristique avec un filtre laplacien. Et comme LoG utilise un filtre gaussien, vous pouvez ajuster son $ \ sigma $ (distribution). Plus le $ \ sigma $ est grand, plus le lissage sera fort, il ne sera donc possible de détecter que les points avec des changements importants. C'est l'inverse, et comme vous l'avez peut-être remarqué, cela joue le même rôle que la simple manipulation du grossissement.

CSE/EE486 Computer Vision I, Lecture 11, LoG Edge and Blob Finding, p19

SIFT détecte les points caractéristiques en préparant plusieurs couches ajustées pour ce $ \ sigma $ (espace d'échelle). Ce qui suit est la figure.

Ici, afin de simplifier le calcul de LoG, l'approximation est effectuée par la différence entre les deux couches avec des $ \ sigma $ différents. C'est le DoG (Différence de Gaussien). Les points caractéristiques trouvés sont comparés aux échelles précédente et suivante pour voir s'ils sont robustes par rapport à l'échelle (par rapport à 8 points autour et 9 points chacun sur les échelles avant et arrière, pour un total de 26 points).

Vous pouvez maintenant voir les fonctionnalités robustes de la balance. Le reste correspond à la "force" et à la "direction" de la quantité de changement à ce point caractéristique, qui est obtenue à partir de la quantité de changement et de son angle.

Ici, SIFT considère non seulement un seul point caractéristique, mais aussi une masse 16 * 16 centrée sur celui-ci (la taille de cette "masse" est appelée [taille du bac](http: // www). .vlfeat.org / api / sift.html)).

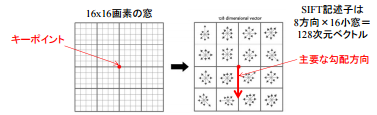Traitement multimédia sémantique A2, p4

Divisez-le en zones 4x4 et créez un histogramme avec l'axe vertical comme quantité de changement (magnitude de la quantité de changement) et l'axe horizontal comme direction (= l'angle du gradient de la quantité de changement).

CSE/EE486 Computer Vision I, Lecture 31, Object Recognition : SIFT Keys, p24

La figure ci-dessus se résume de 0 à 36 (correspondant à 360 degrés), mais finalement elle se résume en 8 directions. Ensuite, vous aurez un vecteur dans lequel chaque fenêtre 4 * 4 a des éléments dans 8 directions. Ce vecteur à 128 dimensions est le vecteur SIFT, qui est une description de point caractéristique avec trois caractéristiques: il est robuste à «l'échelle», et la «force» et la «direction» peuvent être connues.

En utilisant ce vecteur SIFT, il devient possible de faire correspondre des points caractéristiques avec une précision extrêmement élevée.

Évolution de la méthode de détection des points caractéristiques

Les méthodes de détection et de description des points caractéristiques énumérées ci-dessus évoluent d'année en année. Voici l'évolution de la méthode avant et après l'apparition du SIFT. Vous pouvez voir le processus d'obtention de fonctionnalités résistantes à la rotation et à l'échelle.

Tutoriel MIRU2013: SIFT et approches ultérieures, p5

C'est l'évolution après SIFT. Une technique appelée SURF, qui accélère le SIFT, est également souvent utilisée. Les deux SIFT et SURF sont brevetés **. SIFT brevet expiré le 6 mars 2020, et même OpenCV [hors NON GRATUIT](https://github.com/ opencv / opencv_contrib / pull / 2449), mais il existe toujours une taxe de brevet pour l'utilisation de SURF. Par conséquent, j'ai expliqué jusqu'à présent, mais il semble que ORB et AKAZE ajoutés dans OpenCV 3.0 soient bons pour une utilisation réelle. Rien n'est plus rapide que SIFT / SURF.

Tutoriel MIRU2013: SIFT et approches ultérieures, p93

Si vous comprenez les méthodes de base introduites cette fois, il sera plus facile de comprendre ce qui a été amélioré lorsque de nouvelles méthodes apparaissent dans le futur.

Correspondance des points caractéristiques

Les points caractéristiques détectés peuvent être utilisés à diverses fins. À titre d'exemple typique, je voudrais présenter la méthode utilisée pour la correspondance d'images.

Tout d'abord, lors de la mise en correspondance d'images, le flux de base consiste à découper la zone autour du point caractéristique à comparer (cette découpe s'appelle un patch) et à vérifier si elle se trouve également dans l'autre image. Devenir. Il existe deux types d'utilisation de ce patch:

Basé sur un modèle: vérifiez l'autre image pour une correspondance avec le patch
Basé sur les fonctionnalités: extraire des fonctionnalités d'un patch et voir s'il y a des correspondances pour ces fonctionnalités

L'image est comme indiqué dans la figure ci-dessous.

Dans tous les cas, lors d'une comparaison, vous avez besoin d'une fonction pour mesurer la similitude. * Comme il est difficile de calculer la similitude pour toute la plage de l'image, il est nécessaire de restreindre la plage de recherche, mais je n'y toucherai pas ici.

Voici des indicateurs typiques pour mesurer la similitude.

SSD (somme des différences au carré): somme des différences au carré
NCC (corrélation croisée normalisée): corrélation croisée normalisée

** SSD ** est l'index le plus simple, et si vous regardez la différence entre les modèles et les fonctionnalités et qu'il est proche de 0, il est considéré comme similaire. Pour la distance à parcourir, c'est-à-dire le seuil, le rapport au point caractéristique le plus correspondant est souvent utilisé. ** NCC **, ou intercorrélation, est une mesure de similitude et peut être obtenue en calculant le produit interne. Par exemple, si les vecteurs sont totalement indépendants (= indépendants les uns des autres), ils doivent être orthogonaux et le produit interne des vecteurs orthogonaux sera 0. Au contraire, s'il est différent de 0, il existe une corrélation positive / négative. Ensuite, l'intercorrélation normalisée est obtenue en normalisant (moyenne 0, variance 1) puis en prenant la corrélation mutuelle.

J'écrirai aussi une formule

SSD(I_1, I_2) = \sum_{[x, y] \in R} (I_1(x, y) - I_2(x, y))^2 \\
C(I_1, I_2) = \sum_{[x, y] \in R} I_1(x, y) I_2(x, y) \\
NCC(I_1, I_2) = \frac{1}{n - 1}\sum_{[x, y] \in R} \frac{(I_1(x, y) - \mu_1)}{\sigma_1} \cdot \frac{(I_2(x, y) - \mu_2)}{\sigma_2}

NCC est un processus qui est filtré par modèle en raison de la nature de la prise du produit interne. Ce qui suit est un exemple de traitement réel, et vous pouvez voir que la partie qui correspond au modèle réagit.

CSE/EE486 Computer Vision I, Lecture 7, Template Matching, p7

Si vous souhaitez effectuer une correspondance plus stricte, vous pouvez faire correspondre non seulement A-> B mais aussi B-> A et n'utiliser que ceux qui sont jugés correspondre des deux côtés. En utilisant cette correspondance des points caractéristiques, il est possible de créer des photos panoramiques, de classer et de rechercher des images.

Implémentation dans OpenCV

Enfin, je présenterai comment l'implémenter dans OpenCV. J'ai un exemple écrit dans le bloc-notes Jupyter dans le référentiel suivant.

icoxfog417/cv_tutorial_feature

Bien qu'il s'agisse d'une installation d'OpenCV, Anaconda (conda) est recommandé pour Windows. Non seulement numpy et matplotlib, mais aussi OpenCV lui-même peuvent être installés en une seule fois à partir de ce qui suit.

menpo/Packages/opencv3

Pour la mise en œuvre, je me suis référé au tutoriel officiel OpenCV suivant.

Le code que vous écrivez ne fait que quelques lignes, mais il ne détecte souvent pas bien sans ajustement de paramètres (en particulier SIFT), et les ajustements de paramètres nécessitent toujours une compréhension théorique. En ce sens, je pense qu'une compréhension théorique est indispensable pour maîtriser OpenCV au vrai sens du terme.

Nous espérons que les explications introduites cette fois vous aideront à résoudre la pétrification et à devenir un véritable maître du traitement d'image.

Tendances de la recherche

Récemment, le réseau de neurones convolutionnels (CNN) est apparu, et en termes d'extraction de caractéristiques à partir d'images, je pense que la première chose à se soucier est de savoir quelle est la meilleure, l'ancienne méthode ou CNN. Tout d'abord, je voudrais présenter une enquête sur ce point.

CNN a encore un certain handicap en termes d'apprentissage requis et de vitesse de traitement, mais il est toujours fort en ce sens qu'il peut effectuer diverses tâches avec une grande précision. De nombreuses idées contenues dans les méthodes représentées par SIFT sont toujours utiles, il est donc proposé dans l'article ci-dessus que vous puissiez aller plus haut en les combinant.

Voici des études sur l'extraction de caractéristiques à l'aide de DNN.

OverFeat: Integrated Recognition, Localization and Detection using Convolutional Networks (ICLR, 2014)
La méthode qui a pris la première place dans la tâche de reconnaissance de zone d'ImageNet 2013. Au lieu d'utiliser simplement la carte des caractéristiques de CNN, plusieurs types de regroupement avec un léger décalage (différents décalages) sont appliqués et les résultats sont intégrés. Cela le rend robuste contre le désalignement. La mise en œuvre est disponible sur GitHub
Discriminative Learning of Deep Convolutional Feature Point Descriptors (ICCV, 2015)
Une méthode pour entrer deux correctifs d'image et les entraîner avec une erreur (similaire ou différente) entre eux.
Vous pouvez voir l'implémentation de GitHub sur la page ci-dessus.
Il existe également une étude du même auteur intitulée Extracting features of fashion images.
Adversarial Autoencoders (2015)
L'application du GAN, qui a prévalu dans la génération d'images, progresse également. Celui-ci utilise le GAN pour calculer la différence entre la distribution normale et l'échantillon, qui était le point faible de la VAE. Cliquez ici pour un résumé.
PN-Net: Conjoined Triple Deep Network for Learning Local Image Descriptors (2016)
Une méthode d'apprentissage avec une image et un ensemble d'images positives / négatives (Triple) pour cela, avec une idée similaire à Discriminative ~
Il semble qu'une version améliorée ait été annoncée. Cela s'appelle tfeat (BMVC, 2016), et l'implémentation TensorFlow a été publiée. Il existe également une démonstration de reconnaissance de zone en temps réel.
LIFT: Learned Invariant Feature Points (ECCV, 2016)
Détection de point de caractéristique -> estimation de l'angle (rotation) -> acquisition de description de quantité de caractéristique (indépendante de l'angle), qui est les 3 processus de base de détection de caractéristique, réalisée en combinant CNN.
Adversarial Feature Learning (NIPS 2016 Workshop)
Proposition d'un mécanisme GAN bidirectionnel (BiGAN) qui tente d'acquérir les caractéristiques capturées par le GAN par rétro-calcul en appliquant Adversarial Son utilisation elle-même pourrait également être utilisée dans d'autres domaines.
Une étude similaire est l 'Inference apprise par opposition. Comme vous pouvez le voir sur le site de commentaires, l'idée est presque la même.

Les références

Vision par ordinateur pratique L'explication est honnêtement assez directe, et je pense qu'il est difficile pour les débutants de comprendre cela seuls.
Computer Vision I
Cours de vision par ordinateur à la Pennsylvania State University. Très poli et facile à comprendre
Mobile Computer Vision
Cours de vision par ordinateur mobile de Stanford. Pendant un moment à partir de l'introduction, nous expliquerons comment développer Android, et de Stitching + Blending à Computer Vision. Particulièrement recommandé pour ceux qui souhaitent l'intégrer dans le mobile.
Officiel OpenCV C'est assez simple et possède un exemple de code basé sur OpenCV. Conseillé.
Matériel de l'École supérieure des sciences de l'information et de l'ingénierie, Université des télécommunications L'histoire du traitement d'image du 9. Riche en illustrations et facile à comprendre. Voici les bases de la différenciation d'image la plus élémentaire.
Semantic Multimedia Processing A2 (15 octobre 2013) Cliquez ici pour comprendre SIFT. Très facile à comprendre
Tutoriel MIRU2013: SIFT et approches ultérieures Bien que l'explication soit centrée sur le SIFT, le contexte systématique et historique de la méthode est organisé dans la seconde moitié (92-).
VLFeat Documentation
Document de la bibliothèque d'extraction de points caractéristiques d'images utilisables en C etc. Anglais mais assez facile à comprendre.
Can any one help me understand Deeply SIFT ?
Introduction aux vecteurs propres, analyse en composantes principales, covariance, entropie
[Recherche d'image (reconnaissance d'objets spécifiques) - Méthode classique, correspondance, apprentissage en profondeur, Kaggle](https://speakerdeck.com/smly/hua-xiang-jian-suo-te-ding-wu-ti-ren-shi -gu-dian-shou-fa-matutingu-shen-ceng-xue-xi-kaggle? slide = 115)
Un document qui résume la méthode classique introduite dans cet article pour la dernière méthode basée sur CNN pour l'extraction de caractéristiques à partir d'images.

[PYTHON] Aiguille en or pour quand elle devient une pierre en regardant la formule du traitement d'image