[PYTHON] Accélération du calcul numérique avec NumPy / SciPy: Application 1
Cible
Il est écrit pour les débutants de Python et NumPy. Il peut être particulièrement utile pour ceux qui visent le calcul numérique de systèmes physiques correspondant à "Je peux utiliser le langage C mais j'ai récemment commencé Python" ou "Je ne comprends pas comment écrire comme Python". Peut être.
De plus, il peut y avoir des descriptions incorrectes en raison de mon manque d'étude. Veuillez me pardonner.
Résumé
Le contenu est une continuation de Accélérer le calcul numérique avec NumPy: Basics. Pour boucle autant que possible en utilisant les fonctions universelles et les opérations de ndarray Je vais mettre en œuvre le calcul numérique de base sans utiliser. SciPy rejoindra le groupe à partir de ce moment. Je n'ai pas beaucoup commenté la mise en œuvre détaillée des fonctions NumPy / SciPy ci-dessous, donc si vous avez des questions, n'hésitez pas à nous contacter. Veuillez lire la référence. Inutile de dire, ** Il est très important de ne pas réinventer les roues. **
différentiel
Les équations de base de la physique sont accompagnées d'une différenciation. La différenciation étant une application linéaire, elle peut être décrite par une équation matricielle. Par exemple, disons que nous calculons la double différenciation d'une fonction. Nous l'exprimerons en utilisant la différence directe et la différence arrière. Masu:
\frac{d^2}{dx^2}\psi(x) = \frac{\psi(x + \Delta x) - 2\psi(x) + \psi(x - \Delta x)}{\Delta x^2} + {\cal O}(\Delta x^2)
Si vous dispersez $ \ psi (x) $ avec $ \ Delta x $
\psi(x)\rightarrow \{\psi(x_0), \psi(x_1), ..., \psi(x_{n-1}), \psi(x_n)\} = \{\psi_0, \psi_1, ..., \psi_{n-1}, \psi_n\}\hspace{1cm}x_i = -L/2 + i\Delta x
Les différences peuvent être écrites sous forme matricielle:
\frac{d^2}{dx^2}\psi(x) = \frac{1}{\Delta x^2}
\begin{pmatrix}
\psi_{-1} -2\psi_0 + \psi_1\\
\psi_0 -2\psi_1 + \psi_2\\
\vdots\\
\psi_{n-2} -2\psi_{n-1} + \psi_n\\
\psi_{n-1} -2\psi_n + \psi_{n+1}
\end{pmatrix}
\simeq \frac{1}{\Delta x^2}
\begin{pmatrix}
-2&1&0&\cdots&0\\
1&-2 &1&&0\\
0 & 1&-2&& \vdots\\
\vdots&&&\ddots&1\\
0& \cdots& 0 &1& -2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix}
=K\psi
Il y a quelque chose de désagréable à ce sujet, mais ce n'est pas grave si $ \ Delta x $ est petit. Maintenant, c'est ici si vous pouvez faire une file d'attente.
la mise en oeuvre
Je vais l'implémenter en Python. Je vais préparer quelques fonctions initiales et les différencier:
>>> import numpy as np
>>> def f(x):
... return np.exp(-x**2)
...
>>> L, N = 7, 100
>>> x = np.linspace(-L/2, L/2, N)
>>> psi = f(x)
>>> psi
array([ 4.78511739e-06, 7.81043424e-06, 1.26216247e-05,
2.01935578e-05, 3.19865883e-05, 5.01626530e-05,
7.78844169e-05, 1.19723153e-04, 1.82206228e-04,
...,
2.74540100e-04, 1.82206228e-04, 1.19723153e-04,
7.78844169e-05, 5.01626530e-05, 3.19865883e-05,
2.01935578e-05, 1.26216247e-05, 7.81043424e-06,
4.78511739e-06])
Et nous avons une matrice de différenciation. Pour ce faire, nous devons stocker les valeurs dans la composante diagonale inférieure. ** Nous combinons donc la tranche de ndarray avec np.vstack **:
>>> K = np.eye(N, N)
>>> K
array([[ 1., 0., 0., ..., 0., 0., 0.],
[ 0., 1., 0., ..., 0., 0., 0.],
[ 0., 0., 1., ..., 0., 0., 0.],
...,
[ 0., 0., 0., ..., 1., 0., 0.],
[ 0., 0., 0., ..., 0., 1., 0.],
[ 0., 0., 0., ..., 0., 0., 1.]])
>>> K_sub = np.vstack((K[1:], np.array([0] * N)))
>>> K_sub
array([[ 0., 1., 0., ..., 0., 0., 0.],
[ 0., 0., 1., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 0., 0., 0.],
...,
[ 0., 0., 0., ..., 0., 1., 0.],
[ 0., 0., 0., ..., 0., 0., 1.],
[ 0., 0., 0., ..., 0., 0., 0.]])
>>> K = -2 * K + K_sub + K_sub.T
>>> K
array([[-2., 1., 0., ..., 0., 0., 0.],
[ 1., -2., 1., ..., 0., 0., 0.],
[ 0., 1., -2., ..., 0., 0., 0.],
...,
[ 0., 0., 0., ..., -2., 1., 0.],
[ 0., 0., 0., ..., 1., -2., 1.],
[ 0., 0., 0., ..., 0., 1., -2.]])
Si vous prenez le produit avec cela, la différenciation de la deuxième commande est terminée:
dx = L/N
psi_2dot = dx**-2 * np.dot(K, psi)
Je pourrais l'écrire sans utiliser la boucle for. Pendant ce temps, ** il existe en fait une fonction pour calculer le dégradé appelée gradient **:
psi_dot_np = np.gradient(psi, dx)
psi_2dot_np = np.gradient(psi_dot_np, dx)
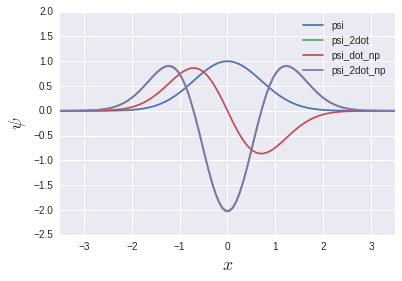
psi_2dot et psi_2dot_np se chevauchent presque complètement. Vous pourriez penser que l'histoire de la matrice précédente n'a aucun sens, mais nous reverrons la lumière du jour dans un chapitre ultérieur sur les équations aux valeurs propres. Sera.
L'intégration
Un algorithme bien connu pour l'intégration numérique serait l'intégration Simpson:
\int_a^b dx\; f(x) = \sum_{i=0}^{n-1}\frac{h}{6}\left[f(x_i) + 4f\left(x_i + \frac{h}{2}\right) + f(x_i + h)\right]\hspace{1cm}x_i = a + ih
La preuve est simple avec Lagrange Completion, mais je vais l'omettre ici.
la mise en oeuvre
La mise en œuvre ressemblerait à ceci:
>>> simp_arr = f(x) + 4 * f(x + dx / 2) + f(x + dx)
>>> dx / 6 * np.sum(simp_arr)
1.75472827313
J'aime la simplicité de mettre l'expression dans le code telle quelle. ** Cependant, l'intégration Simpson est fournie en fonction de SciPy: **
>>> from scipy.integrate import simps
>>> simps(psi, x)
1.7724525416390826
Les résultats du calcul sont légèrement différents car SciPy utilise la règle Simpson, qui est plus précise. Sauf si vous avez une raison spécifique, il vaut mieux l'utiliser que de la construire vous-même. ** De plus, la différenciation Il existe également une fonction qui passe et intègre la fonction précédente: **
>>> from scipy.integrate import quad
>>> quad(f, -np.inf, np.inf)
(1.7724538509055159, 1.4202636780944923e-08)
Il peut être calculé en donnant une fonction et un intervalle d'intégration. La valeur de retour est tuple, le premier composant est le résultat de l'intégration et le deuxième composant est l'erreur absolue. Quad utilise la technique de la bibliothèque Fortran QUADPACK. Il semble [^ 1]. ** En fait, cet enfant est très bon. ** Voici certaines choses pour lesquelles je suis reconnaissant:
- ** Semble utiliser une intégration adaptative qui change la largeur extrême selon les besoins **
Dans le cas de l'intégration Simpson, la largeur de la différence est uniforme dans l'espace, mais dans le cas de l'intégration adaptative, «où de fines différences sont requises (où la fonction se déplace violemment) sont bonnes, et où il n'y a pas grand besoin (le mouvement de la fonction est). Il semble que cela fasse quelque chose comme "élargir la largeur (dans un endroit calme)". Le calcul s'accélère tout en maintenant la précision de l'erreur. Vous ne vous sentirez peut-être pas si reconnaissant avec une intégration unidimensionnelle ordinaire. Cependant, quand il s'agit de double et triple intégration, c'est incomparablement plus rapide que l'intégration Simpson [^ 2]. C'est beaucoup plus rapide que l'intégration Simpson faite par moi-même en C / C ++.
- ** Vous pouvez donner
np.infà l'intervalle d'intégration **
Pour une fonction compacte comme celle-ci, l'intervalle d'intégration pris dépend de la précision de calcul requise, mais en utilisant
np.inf, la précision du calcul est un argument dequadsans se soucier de la coupure. Il est bon de le lancer dans ʻepsabs, epsrel`, etc.
- ** Facile à utiliser **
Probablement une interface beaucoup plus simple que de toucher directement QUADPACK [^ 3].
Équation de valeur intrinsèque
Parlons maintenant de la mécanique quantique. Trouvons les fonctions propres et les valeurs propres d'énergie d'un système d'oscillateur harmonique unidimensionnel. Hamiltonien
H = \frac{\hat{p}^2}{2} + \frac{\hat{q}^2}{2} = -\frac12\frac{d^2}{dq^2} + \frac{q^2}{2}
Ceci est un enfant. Il utilise un système unitaire de $ \ hbar = \ omega = m = 1 $. Équation de Schroedinger pour cet hamiltonien
H\psi_\ell(q) = E_\ell\psi_\ell(q)
$ \ Ell $ n'est pas l'indice de la différence, mais l'indice de la valeur propre / fonction propre. Premièrement, le terme potentiel est différencié dans un format matriciel:
\frac{q^2}{2}\psi(q) \rightarrow \frac12
\begin{pmatrix}
q_0^2&0&0&\cdots&0\\
0&q_1^2 &0&\cdots&0\\
0 & 0&q_2^2&& \vdots\\
\vdots&&&\ddots&0\\
0& \cdots& 0 &0& q_n^2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix}=\frac12
\begin{pmatrix}
(-L/2)^2&0&0&\cdots&0\\
0&(-L/2 + \Delta q)^2 &0&&0\\
0 & 0&(-L/2 + 2\Delta q)^2&& \vdots\\
\vdots&&&\ddots&0\\
0& \cdots& 0 &0& (L/2)^2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix} = V\psi
Je ne sais pas si ce sera exactement $ L / 2 $, mais c'est vrai.
H\psi = (K + V)\psi = \frac12
\begin{pmatrix}
\frac{2}{\Delta q^2} + (-L/2)^2&\frac{-1}{\Delta q^2}&0&\cdots&0\\
\frac{-1}{\Delta q^2}&\frac{2}{\Delta q^2} + (-L/2 + \Delta q)^2 &\frac{-1}{\Delta q^2}&&0\\
0 & \frac{-1}{\Delta q^2}&\frac{2}{\Delta q^2} + (-L/2 + 2\Delta q)^2&& \vdots\\
\vdots&&&\ddots&\frac{-1}{\Delta q^2}\\
0& \cdots& 0 &\frac{-1}{\Delta q^2}& \frac{2}{\Delta q^2} + (L/2)^2
\end{pmatrix}
\begin{pmatrix}
\psi_0\\
\psi_1\\
\vdots\\
\psi_{n-1}\\
\psi_n
\end{pmatrix} = E_\ell\psi
On dirait.
la mise en oeuvre
Maintenant, c'est du codage.
#Les paramètres du système
>>> L, N = 10, 200
>>> x, dx = np.linspace(-L/2, L/2, N), L / N
#Terme d'exercice K
>>> K = np.eye(N, N)
>>> K_sub = np.vstack((K[1:], np.array([0] * N)))
>>> K = dx**-2 * (2 * K - K_sub - K_sub.T)
#Terme potentiel
>>> V = np.diag(np.linspace(-L/2, L/2, N)**2)
#Équation des valeurs propres de la matrice Hermeet
#w est une valeur unique,v est le vecteur propre
>>> H = (K + V) / 2
>>> w, v = np.linalg.eigh(H)
La définition de dx est subtile, mais ne vous inquiétez pas:
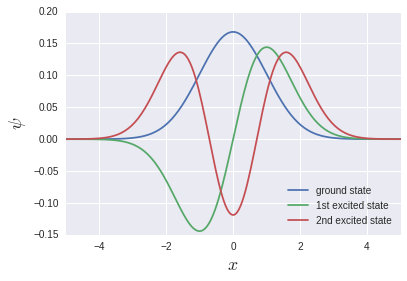
Les fonctions uniques qui sont souvent vues dans les manuels sont produites.
np.linalg.eigh est un solveur de l'équation des valeurs propres pour Elmeet, qui renvoie la valeur propre et la fonction propre. Cette fois, il s'agit d'une matrice triple diagonale, donc il peut s'agir de np.linalg.eig_banded pour la matrice de bande. Cependant, je pense que la vitesse est plutôt plus rapide dans np.linalg.eigh [^ 4]. La consommation de mémoire est probablement moindre dans np.linalg.eig_banded.
** Il convient de noter ici que l'état fondamental, premier état excité, second état excité ... sont stockés dans v [0], v [1], v [2] ... Au lieu de cela, cela signifie vT [0], vT [1], vT [2] .... ** Cela signifie que le stockage des données du tableau en mémoire est Row-major pour le système C et Fortran pour Fortran. Probablement à cause de la différence de colonne majeure. Si np.linalg.eigh est un wrapper pour LAPACK, cela peut être un comportement naturel dans un sens.
Calculons la différence entre les valeurs propres et examinons l'énergie d'excitation. Sortons environ 20 à partir de la base:
>>> np.diff(w)[:20]
[ 1.00470938 1.00439356 1.00407832 1.00376982 1.00351013 1.00351647
1.00464172 1.00938694 1.02300462 1.05279364 1.10422331 1.17688369
1.26494763 1.36132769 1.46086643 1.56082387 1.66005567 1.75820017
1.85521207 1.95115074]
L'énergie d'excitation du système d'oscillateur harmonique est $ \ hbar \ omega $ quel que soit le niveau, donc elle est de 1 dans ce système unitaire. Elle se reproduit assez bien dans la région basse énergie, mais elle devient assez suspecte dans la région haute énergie. Essayons de sortir le 15e état excité:
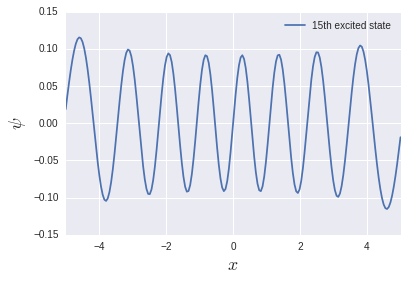
Il y a 15 nœuds, mais la fonction n'est pas compacte au bord. C'est pourquoi la taille d'espace de $ L = 10 $ n'était pas suffisante. Je veux calculer exactement quel état d'excitation. Il est nécessaire de changer la taille de l'espace et le nombre de divisions.
Le calcul analytique des valeurs propres et des fonctions propres d'un oscillateur harmonique est une tâche assez laborieuse, mais il est très simple de se lancer dans des calculs numériques [^ 5].
Équation différentielle
Équation de diffusion unidimensionnelle
\frac{\partial}{\partial t}f(x, t) = \frac{\partial^2}{\partial x^2}f(x, t)
Cet enfant peut trouver une solution analytique par la transformation de Fourier de $ x $ étant donné les conditions initiales [^ 6], mais bien sûr, résolvons-la numériquement. Donnez les conditions en gaussien et commencez par la différenciation spatiale habituelle:
f(x, 0) = \exp(-x^2)\\
f_k \equiv f(k\Delta x, t), \hspace{0.7cm} \Delta x = L/N
Ensuite, les équations différentielles seront également différenciées:
\frac{d}{dt}f_0 = \frac{f_1 - 2f_0}{\Delta x^2}\\
\frac{d}{dt}f_1 = \frac{f_2 - 2f_1 + f_0}{\Delta x^2}
...\\
\frac{d}{dt}f_k = \frac{f_{k+1} - 2f_k + f_{k-1}}{\Delta x^2}\\
...\\
\frac{d}{dt}f_{n-1} = \frac{f_{n} - 2f_{n-1} + f_{n-2}}{\Delta x^2}\\
\frac{d}{dt}f_n = \frac{-2f_n + f_{n-1}}{\Delta x^2}
SciPy prend une liste de différenciations d'une fonction [f0, f1, ..., fn-1, fn] comme argument, et la liste après expansion de temps par $ \ Delta t $ (ndarray) Il existe un solveur de l'équation différentielle appelé ** ʻodeint` qui peut résoudre l'équation différentielle en passant une fonction qui retourne
la mise en oeuvre
Créons d'abord cette fonction:
from scipy.integrate import odeint
def equation(f, t=0, N, L):
dx = L / N
gamma = dx**-2
i = np.arange(1, N, 1)
# f0
arr = np.array(gamma * (f[1] - 2 * f[0]))
# f1 to fN-1
arr = np.append(arr, gamma * (f[i+1] - 2 * f[i] + f[i-1]))
# fN
arr = np.append(arr, gamma * (-2 * f[N] + f[N-1]))
return arr
Vous saurez en quelque sorte ce que vous faites. Dans cette fonction, nous écrirons le $ f $ différencié sous la forme d'un tableau comme f [n]. F isf [0] Il se compose de $ N + 1 $ éléments deà f [N]. De plus, la liste f qui différenciait la fonction est définie dans le premier argument, et l'heure t est définie dans le deuxième argument. Est la spécification de ʻodeint. Assurez-vous d'utiliser cet ordre. L'heure initiale est bien sûr $ t = 0 $, donc la valeur par défaut est définie. ** # f1 à fN-1Au fait, sans écrire[gamma * (f [j + 1] -2 * f [j] + f [j-1]) pour j dans i], listez simplement ʻi qui est ndarray. Je pense que c'est sobre que ce soit juste de le mettre dans l'index de. **
** --Ajout (2016/12/3) - ** Après tout, ce n'est qu'une différenciation de second ordre
from scipy.integrate import odeint
def equation(f, t=0, N, L):
dx = L / N
arr = np.gradient(np.gradient(f, dx), dx)
return arr
C'est bien. «Gradient» est différent de «diff», et il est merveilleux que la taille de la liste ne change pas après le traitement. ** - Ajout ici - **
À propos, la fonction initiale est
def f(x):
return np.exp(-x**2)
C'était.
De plus, certaines variables doivent être passées à ʻodeintlui-même: l'une est ʻequation (f, t0, ...)définie ci-dessus et la seconde est ndarray, qui est la différence entre les fonctions initiales. "(Il semble que l'itérable soit bon), le troisième est une liste du temps" t "à calculer. De plus, comme" équation "a des variables autres que" f "et" t0 ", leur existence" Je dois dire odeint, donc je stocke ces informations dans ʻargs`. Codé avec ceux-ci à l'esprit:
# initial parameter(optional)
N, L = 200, 40
# coordinate
q = np.linspace(-L/2, L/2, N)
# initial value for each fk
fk_0 = f(q)
# time
t_max, t_div = 10, 5
t = np.linspace(0, t_max, t_div)
trajectories = odeint(equation, fk_0, t, args=(N, L))
La solution temporelle pour t [i] est stockée dans trajectoires [i]. Maintenant, traçons ceci:

J'ai pu voir comment la gaussienne se répand. Cette fois, j'ai traité de l'équation de diffusion, donc le code était un peu déroutant avec les deux variables $ (x, t) $. L'équation différentielle ordinaire à une variable Je pense que ce serait plus simple. J'utilise des boucles for lors du traçage, mais ... c'est très bien. Il est important de ne pas utiliser de boucles for (y compris les inclusions de liste) dans le processus de calcul numérique.
en conclusion
Cela fait longtemps, je vais donc résumer le reste dans un autre article. Si quelqu'un dit "Il y a un meilleur moyen!", Je vous serais reconnaissant de bien vouloir commenter.
Vous pouvez voir que NumPy et SciPy ont une plus large gamme de défense que ce à quoi je m'attendais. Quand j'ai cherché une référence en pensant "Peut-être ...", j'avais déjà quelque chose que j'avais mis en œuvre moi-même [^ 7] C'est souvent le cas. ** Cela s'applique non seulement à NumPy / SciPy, mais aussi aux modules Python standard. ** Veuillez consulter la référence Python. Vous serez étonné de voir comment cela s'est produit. Je suis sûr qu'il existe un paquet.
** Addendum (2016/11/25): Suite ci-dessous ** Accélération du calcul numérique à l'aide de NumPy / SciPy: Application 2
[^ 1]: Je n'ai pas vérifié s'il enveloppait QUADPACK. Le manuel dit "... en utilisant une technique de la bibliothèque Fortran QUADPACK."
[^ 2]: Je pense que Monte Carlo est plus rapide que 7 ou 8 couches.
[^ 3]: Je ne l'ai pas utilisé, donc honnêtement, je ne sais pas.
[^ 4]: Il semble que le solveur de matrice de bande finisse par étendre ce qui est passé dans la bande dans un format matriciel et ensuite le calcule.Dans ce cas, je sens que la consommation de mémoire ne change pas après tout ... Je ne connais pas les détails. est.
[^ 5]: Bien sûr, le physicien ne doit pas se contenter du calcul numérique, puisque le calcul numérique seul ne peut pas faire une discussion qualitative, même un système qui ne peut être résolu exactement est approché et analytique. Il est très logique de trouver une solution.
[^ 6]: Nous résolvons souvent des équations différentielles par transformation de Laplace dans les circuits électroniques, mais c'est essentiellement la même chose: si nous préparons une fonction initiale qui ne peut pas être intégrée analytiquement, nous finirons par la résoudre numériquement. En ce sens, gaussien est une très bonne fonction compacte, analytiquement intégrable.
[^ 7]: Et souvent bien mieux que ce que j'ai mis en œuvre.
Recommended Posts