[PYTHON] Estimation la plus probable de diverses distributions avec Pyro
Estimation la plus probable de divers paramètres de distribution de probabilité continue unidimensionnelle avec Pyro.
- distribution normale
- Distribution bêta -T distribution
- Distribution Laplace
- Distribution de Cauchy
- Distribution exponentielle
- Distribution Gamma
- Distribution Gambel
Bien que certaines des estimations les plus probables fournissent des solutions analytiques (comme la distribution normale), Certains sont itératifs (comme la distribution gamma). De plus, la méthode diffère selon la distribution et l'implémentation est différente. Faites-le ici en utilisant pyro, Définissez simplement la distribution de probabilité dans le modèle Après cela, l'estimation la plus probable est effectuée par la méthode itérative avec le même code.
Seule la distribution normale sera expliquée en détail. D'autres codes peuvent être trouvés dans l'essentiel ci-dessous. https://gist.github.com/tttamaki/b061f64ad1c0f640acb2bccb88b5087e
Tips
--Utilisez ʻAutoDelta` comme guide (estimation ponctuelle) --Le moniteur pendant l'apprentissage est accroché
- Les estimations sont introduites avec
poutine.trace
Préparation
Préparation. Pour ordinateur portable
import matplotlib.pyplot as plt
%matplotlib inline
from collections import defaultdict
import os
import numpy as np
import torch
import torch.distributions.constraints as constraints
import pyro
from pyro.optim import Adam
import pyro.distributions as dist
from pyro.infer import SVI, Trace_ELBO
from pyro.infer.autoguide import AutoDelta, AutoNormal
from pyro.infer.autoguide.initialization import init_to_feasible
# import pyro.poutine as poutine
from pyro import poutine
pyro.enable_validation(True)
pyro.set_rng_seed(101)
from tqdm.notebook import tqdm
import daft
Distribution normale unidimensionnelle
Vrais paramètres
Créer aléatoirement de vrais m et std
true_m = np.random.rand() * 10
true_std = np.abs(np.random.rand() * 2)
print('m =', true_m, 'std =', true_std)
x_range = np.arange(true_m - 4*true_std, true_m + 4*true_std, 0.01)
x_max = x_range.max()
x_min = x_range.min()
print('x_range: from {0:.3f} to {1:.3f}'.format(x_min, x_max))
python
m = 2.3235366181476067 std = 0.16712286732668735
x_range: from 1.655 to 2.985
Création de données
Échantillonnage de données à partir d'une vraie distribution
# sampling
target_dist = dist.Normal(true_m, true_std)
data = torch.tensor([target_dist() for i in range(100)])
#pdf: fonction de distribution
true_y = [target_dist.log_prob(torch.tensor([x])).exp() for x in x_range]
fig = plt.figure(figsize=(10,5))
plt.plot(x_range, true_y, c='k', label=r'Normal(m,$\sigma$)')
plt.hist(data, range=(x_min, x_max), bins=100, density=True, alpha=0.2, label=r'observed data $\{x_i\}$')
plt.title(r'm={0:.3f} $\sigma$={1:.3f}'.format(true_m, true_std))
plt.ylim(0,)
plt.xlabel('x')
plt.legend()
plt.savefig('obs-data')
plt.show()

À propos, la solution analytique de l'estimation la plus probable est la moyenne et la variance dans le cas de la distribution normale.
python
ml_m = data.numpy().mean()
ml_std = data.numpy().std()
print('m={0:.3f}, sigma={1:.3f}'.format(ml_m, ml_std))
python
m=2.318, sigma=0.157
Modèle graphique
Le modèle «model» a la structure suivante.
p_\theta(X) - $ X = \ {x_1, \ ldots, x_N } $ sont les données observées
- Les paramètres sont $ \ theta = \ {m, \ sigma } $
x_i \sim \mathrm{Gauss}(m, \sigma)

Dessinez un modèle graphique avec daft
pgm = daft.PGM()
pgm.add_node("xn", r"$x_n$", 2, 1, observed=True)
pgm.add_node("m", "m", 1.5, 2, fixed=True)
pgm.add_node("std", r"$\sigma$", 2.5, 2, fixed=True)
pgm.add_edge("m", "xn")
pgm.add_edge("std", "xn")
pgm.add_plate([1, 0.5, 2, 1], label=r"$n = 1, \ldots, N$", shift=-0.2)
pgm.show() # render and show
Modèles et guides
Pour le modèle, définissez m et std comme paramètres dans pyro.param.
modèle
def model(data=None):
#La valeur initiale estimée est 0.Mettre à 0
m = pyro.param("m", torch.tensor(0.0))
#La valeur initiale estimée est 1.Mettre à 0
# std >Puisqu'il vaut 0, ajoutez une contrainte positive
std = pyro.param("std", torch.tensor(1.0), constraint=constraints.positive)
#data représente toutes les données (c.-à-d. tableau de liste vectorielle)
with pyro.plate('observe_data'): #Étant donné que chaque obs
pyro.sample('obs', dist.Normal(m, std), obs=data) # vector-Utiliser la plaque
Utilisez l'estimation des points AutoDelta pour vous guider
python
guide = AutoDelta(
poutine.block(model, hide=['obs']), #Cachez les obs du modèle et utilisez les autres (m et std)
init_loc_fn=init_to_feasible #La valeur initiale est une valeur raisonnable
)
Préparation estimée
python
adam_params = {"lr": 0.005, "betas": (0.95, 0.999)}
optimizer = Adam(adam_params) #Adam pour le moment
svi = SVI(model=model,
guide=guide,
optim=optimizer,
loss=Trace_ELBO()
)
Initialisez les paramètres et définissez les hooks. Pour enregistrer la valeur au milieu du paramètre.
python
pyro.clear_param_store() # pyro.get_param_store()Sera vide
svi.loss(model, guide, data) #Je dois faire ça une fois piro.get_param_store()Est une maman vide
trace_dic = defaultdict(list) #Sauvegardez la valeur (cette liste sera appelée trace ici)
for name, value in pyro.get_param_store().named_parameters():
print('tracing', name, type(value), value)
#hook est appelé pour chaque calcul de gradient. Ignorer la valeur du dégradé grad, utiliser le nom pour param(name)Obtenez la valeur avec et ajoutez-la à la liste de dic
value.register_hook(lambda grad, name=name: trace_dic[name].append(pyro.param(name).item()))
python
tracing m <class 'torch.Tensor'> tensor(0., requires_grad=True)
tracing std <class 'torch.Tensor'> tensor(0., requires_grad=True)
Estimation
Estimation itérative.
python
num_steps = 5000
with tqdm(range(num_steps)) as pbar:
for i,p in enumerate(pbar):
loss = svi.step(data) #Calcul du gradient, mise à jour
trace_dic['loss'].append(loss)
if i > 100 and np.isclose(trace_dic['loss'][-100], loss):
break #Convergence si la valeur ne change pas d'il y a 100 fois
if i % 10 == 0: #Si vous l'affichez à chaque fois, il est trop tôt pour le voir, alors affichez-le une fois toutes les 10 fois
pbar.set_postfix(loss=loss)
État de convergence
python
fig = plt.figure(figsize=(10,5))
plt.plot(trace_dic['loss'])
plt.title("ELBO")
plt.xlabel("step")
plt.ylabel("loss");
savefig("loss")
plt.show()
fig = plt.figure(figsize=(15,5))
for i,param in enumerate(['m', 'std']):
plt.subplot(1,2,i+1)
plt.plot(trace_dic[param])
plt.ylabel(param)
plt.tight_layout()
savefig("params")
plt.show()
État de diminution de la perte

Convergence des paramètres m et std

résultat
Comparaison de la valeur estimée la plus probable et de la valeur réelle
python
trace = poutine.trace(model).get_trace()
print('m', trace.nodes['m']['value'].item(), 'true m', true_m)
print('std', trace.nodes['std']['value'].item(), 'true std', true_std)
C'est proche de la vraie valeur.
python
m 5.083353042602539 true m 5.163986277024462
std 1.1655045747756958 true std 1.1413351737362796
Comparaison de la distribution des estimations les plus probables et de la distribution réelle
python
fig = plt.figure(figsize=(10,5))
#Obtenir des paramètres avec trace
trace = poutine.trace(model).get_trace()
m = trace.nodes['m']['value'].item()
std = trace.nodes['std']['value'].item()
# generate a pdf
estimated_dist = dist.Normal(m, std)
y = [estimated_dist.log_prob(torch.tensor([x])).exp() for x in x_range]
# plot
plt.plot(x_range, y, c='k', label='ML estimated pdf')
plt.plot(x_range, true_y, c='r', label=r'true pdf')
plt.hist(data, range=(x_min, x_max), bins=100, alpha=0.2, density=True, l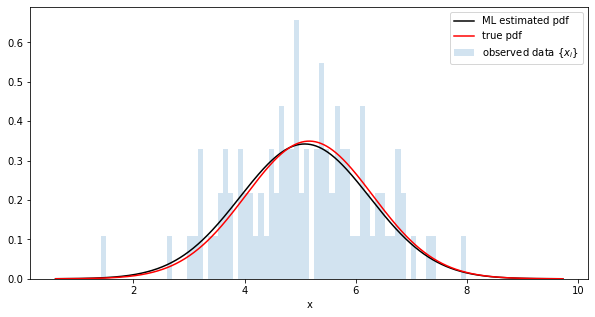
abel=r'observed data $\{x_i\}$')
plt.xlabel('x')
plt.legend()
savefig("sampled-pdf")
plt.show()

Échantillon de la distribution estimée et comparaison avec les données originales
python
fig = plt.figure(figsize=(10,5))
obs = []
for _ in range(5000):
trace = poutine.trace(model).get_trace()
obs.append(trace.nodes['obs']['value'].item())
plt.xlabel('posterior samples')
plt.hist(data, range=(x_min, x_max), bins=100, alpha=0.2, density=True, label=r'observed data $\{x_i\}$')
plt.hist(obs, range=(x_min, x_max), bins=100, alpha=0.2, density=True, color='r', label=r'sampled data$')
plt.legend()
savefig("pdf-obs")
plt.show()

Autres distributions
Ce qui suit ne montre que les données d'origine (bleu), la vraie distribution (rouge) et la distribution estimée avec le paramètre d'estimation le plus probable (noir).
Le code est https://gist.github.com/tttamaki/b061f64ad1c0f640acb2bccb88b5087e C'est dedans.
Distribution bêta

distribution t

Distribution de Laplace

Distribution de Cauchy

Distribution exponentielle

Distribution gamma

Distribution Gambel

Recommended Posts