[PYTHON] Coefficient de corrélation MIC qui peut gérer les relations non linéaires et test d'indépendance de Hilbert-Schmidt HSIC

Le coefficient de corrélation de Pearson est un indice bien connu pour mesurer l'indépendance des variables. Cependant, c'est un indice qui traite des relations linéaires (linéaires), et quand il y a une relation en forme de U telle qu'une fonction quadratique, il est jugé comme "aucune corrélation". MIC et HSIC sont connus comme des indicateurs pour traiter de telles relations non linéaires, j'ai donc essayé d'utiliser le package Python.

Tout le code ci-dessous a été testé avec Google Colaboratory.

Package Python qui calcule le coefficient d'information maximal (MIC)

Vous pouvez installer le pip comme suit:

!pip install minepy

Après l'installation, préparez-vous comme suit.

from minepy import MINE
mine = MINE()

Paquet Python qui calcule HSIC (Hilbert-Schmidt Independence Criterion)

Clonez Git comme suit:

!git clone https://github.com/amber0309/HSIC.git

Préparez-vous comme suit.

from HSIC.HSIC import hsic_gam

Fonction linéaire

Examinons d'abord la fonction linéaire.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

X = np.linspace(-1, 1, 51)
Y = X
plt.scatter(X, Y)

out6.png

Le coefficient de corrélation de Pearson est

np.corrcoef(X, Y)[0, 1]

1.0

MIC est

mine.compute_score(X, Y)
mine.mic()

0.9999999999999998

Plus la valeur suivante est élevée, plus l'indépendance du HSSC est faible, et plus la valeur est petite, plus l'indépendance est élevée.

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

22.610487654066624

Ajoutons du bruit à la fonction linéaire.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = X + np.random.rand(51,)
plt.scatter(X, Y)

out10.png

Le coefficient de corrélation de Pearson est

np.corrcoef(X, Y)[0, 1]

0.9018483832673769

MIC est

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

13.706487127525389

Calculons comment le coefficient de corrélation de Pearson change à mesure que la quantité de bruit augmente petit à petit.

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X + np.random.rand(51,) * d / 10
    D.append(d)
    C.append(np.corrcoef(X, Y)[0, 1])

plt.plot(D, C)

out14.png

De même, calculons comment le MIC change lorsque la quantité de bruit augmente petit à petit.


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X + np.random.rand(51,) * d / 10
    D.append(d)
    mine.compute_score(X, Y)
    C.append(mine.mic())

plt.plot(D, C)

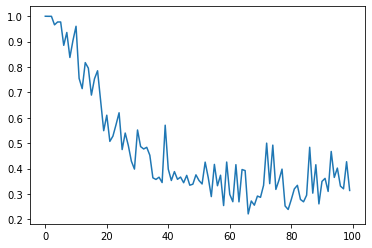
out15.png

De même, calculons comment le HSIC change lorsque la quantité de bruit augmente petit à petit.

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X + np.random.rand(51,) * d / 10
    D.append(d)
    testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
    C.append(testStat / thresh)

plt.plot(D, C)

out16.png

fonction quadratique

Vient ensuite la fonction quadratique.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = X**2
plt.scatter(X, Y)

out17.png

Le coefficient de corrélation de Pearson est

np.corrcoef(X, Y)[0, 1]

-2.3862043230836297e-17

MIC est

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

9.285886928766184

Ajoutons du bruit.

X = np.linspace(-1, 1, 51)
Y = X**2 + np.random.rand(51,)
plt.scatter(X, Y)

out21.png

Le coefficient de corrélation de Pearson est

np.corrcoef(X, Y)[0, 1]

0.04693076570744622

MIC est

mine.compute_score(X, Y)
mine.mic()

0.5071787519579662

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

5.247036645612692

Calculons comment le coefficient de corrélation de Pearson change à mesure que la quantité de bruit augmente petit à petit.


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X**2 + np.random.rand(51,) * d / 10
    D.append(d)
    C.append(np.corrcoef(X, Y)[0, 1])

plt.plot(D, C)

out25.png

De même, calculons comment le MIC change lorsque la quantité de bruit augmente petit à petit.


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X**2 + np.random.rand(51,) * d / 10
    D.append(d)
    mine.compute_score(X, Y)
    C.append(mine.mic())

plt.plot(D, C)

out26.png

De même, calculons comment le HSIC change lorsque le niveau de bruit augmente petit à petit.

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = X**2 + np.random.rand(51,) * d / 10
    D.append(d)
    testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
    C.append(testStat / thresh)

plt.plot(D, C)

out27.png

On peut voir que le coefficient de corrélation de Pearson ne pouvait pas détecter la relation de la fonction quadratique, alors que les MIC et HSIC pouvaient être détectés. Vous pouvez également voir que le MIC ne sera en grande partie pas affecté par les petits bruits.

Fonction trigonométrique

Regardons également la fonction triangulaire.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = np.sin((X)*np.pi*2)
plt.scatter(X, Y)

out39.png

Le coefficient de corrélation de Pearson est

np.corrcoef(X, Y)[0, 1]

-0.37651692742033543

MIC est

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

3.212604441715373

Ajoutons du bruit.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = np.sin((X+0.25)*np.pi*2) + np.random.rand(51,)
plt.scatter(X, Y)

out43.png

Le coefficient de corrélation de Pearson est

np.corrcoef(X, Y)[0, 1]

0.049378342546505014

MIC est

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

1.3135420547013614

Étudiez l'effet de l'augmentation du bruit. Le coefficient de corrélation de Pearson est

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = np.sin((X+0.25)*np.pi*2) + np.random.rand(51,) * d / 10
    D.append(d)
    C.append(np.corrcoef(X, Y)[0, 1])

plt.plot(D, C)

out47.png

MIC est

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = np.sin((X+0.25)*np.pi*2) + np.random.rand(51,) * d / 10
    D.append(d)
    mine.compute_score(X, Y)
    C.append(mine.mic())

plt.plot(D, C)

out48.png

HSIC

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = np.sin((X+0.25)*np.pi*2) + np.random.rand(51,) * d / 10
    D.append(d)
    testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
    C.append(testStat / thresh)

plt.plot(D, C)

out49.png

On s'attendait à ce que le coefficient de corrélation de Pearson ne puisse pas détecter la relation de la fonction triangulaire avec le bruit, mais il semble que HSIC a également abandonné. Parmi eux, j'ai été surpris que MIC ait pu détecter la relation.

Fonction Sigmaid

Enfin, il y a la fonction sigmoïde.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = 1 / (1 + np.exp(-X*10))
plt.scatter(X, Y)

out58.png

Le coefficient de corrélation de Pearson est

np.corrcoef(X, Y)[0, 1]

0.9354020629807919

MIC est

mine.compute_score(X, Y)
mine.mic()

0.9999999999999998

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

27.433932271008874

Ajoutons du bruit.

import numpy as np

X = np.linspace(-1, 1, 51)
Y = 1 / (1 + np.exp(-X*10)) + np.random.rand(51,)
plt.scatter(X, Y)

out62.png

Le coefficient de corrélation de Pearson est

np.corrcoef(X, Y)[0, 1]

0.7994507640548881

MIC est

mine.compute_score(X, Y)
mine.mic()

0.9997226475394071

HSIC

testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
testStat / thresh

12.218008194240534

Voyons l'effet de l'augmentation du bruit. Le coefficient de corrélation de Pearson est


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = 1 / (1 + np.exp(-X*10)) + np.random.rand(51,) * d / 10
    D.append(d)
    C.append(np.corrcoef(X, Y)[0, 1])

plt.plot(D, C)

out66.png

MIC est

D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = 1 / (1 + np.exp(-X*10)) + np.random.rand(51,) * d / 10
    D.append(d)
    mine.compute_score(X, Y)
    C.append(mine.mic())

plt.plot(D, C)

out67.png

HSIC


D = []
C = []
for d in range(100):
    X = np.linspace(-1, 1, 51)
    Y = 1 / (1 + np.exp(-X*10)) + np.random.rand(51,) * d / 10
    D.append(d)
    testStat, thresh = hsic_gam(X.reshape(len(X), 1), Y.reshape(len(Y), 1))
    C.append(testStat / thresh)

plt.plot(D, C)

out68.png

Tous les indicateurs peuvent détecter la relation, mais en termes de résistance au bruit, le MIC semble être le plus fort.

C'est une impression individuelle

MIC MIC!

Recommended Posts

Coefficient de corrélation MIC qui peut gérer les relations non linéaires et test d'indépendance de Hilbert-Schmidt HSIC