[PYTHON] [Statistiques] Visualisez et comprenez la méthode Hamiltonian Monte Carlo avec animation.

Cet article tente de comprendre le principe de fonctionnement de la méthode Hamiltonian Monte Carlo (HMC) à l'aide de l'animation. Ceci est une suite de l'article de l'autre jour, "[Statistiques] Je vais expliquer l'échantillonnage par la méthode de Monte Carlo en chaîne de Markov (MCMC) avec animation."](Http://qiita.com/kenmatsu4/items/55e78cc7a5ae2756f9da).

J'ai utilisé l'exemple du livre du professeur Toyoda "Bayes Statistics from the Basics". La distribution à échantillonner sera cette fois la distribution gamma. Cet article ne donne qu'une explication théorique des pièces utilisées pour l'animation, veuillez donc vous référer à ce livre pour une explication détaillée de la console HMC.

introduction

La cible à estimer est la distribution gamma avec $ \ theta $ comme variable. Puisque les paramètres à estimer par l'estimation bayésienne sont représentés par $ \ theta $, ils sont représentés par une distribution de $ \ theta $. [^ 1]

[^ 1]: La distribution gamma est une distribution relativement simple qui peut fournir des informations suffisantes telle quelle, mais ici nous supposerons qu'il s'agissait d'une distribution postérieure difficile. À partir de cette distribution postérieure, nous allons générer des nombres aléatoires en utilisant HMC et essayer de trouver les informations de la distribution postérieure à partir de la séquence de nombres aléatoires obtenue.

Voici la distribution gamma. $ f(\theta|\alpha, \lambda) = {\lambda^{\alpha} \over \Gamma(\alpha)} \theta^{\alpha-1}e^{-\lambda \theta} \quad \quad 0 \le x,\quad 0 < \lambda,\quad 0 < \alpha $

En se concentrant uniquement sur la partie noyau de cette distribution gamma à l'exclusion de la constante de normalisation, $ f(\theta|x) \propto e^{-\lambda \theta} \theta ^{\alpha -1} $ Ce sera.

Dans la console HMC, cela est consigné et multiplié par moins, c'est-à-dire $h(\theta) = -\log (f(\theta|x)) = \lambda \theta - (\alpha -1) \log(\theta) $ Est équivalent à l'énergie de position en physique. Cette fois, nous utiliserons $ \ alpha = 11, \ lambda = 13 $ pour les paramètres. Le graphique ressemble à celui ci-dessous.

Hamiltonien dérivé de la relation entre l'énergie de position $ h (\ theta) $ et l'énergie cinétique $ p $ $H(\theta, p) = h(\theta) + {1 \over 2} p^2$ Cependant, compte tenu de la propriété qu'elle devient constante à moins qu'une force externe ne soit appliquée, il existe une relation dans laquelle l'énergie cinétique augmente à mesure que l'énergie de position diminue. La figure ci-dessus est une animation de cette situation. La longueur de la flèche rouge indique la magnitude de l'énergie cinétique $ p $.

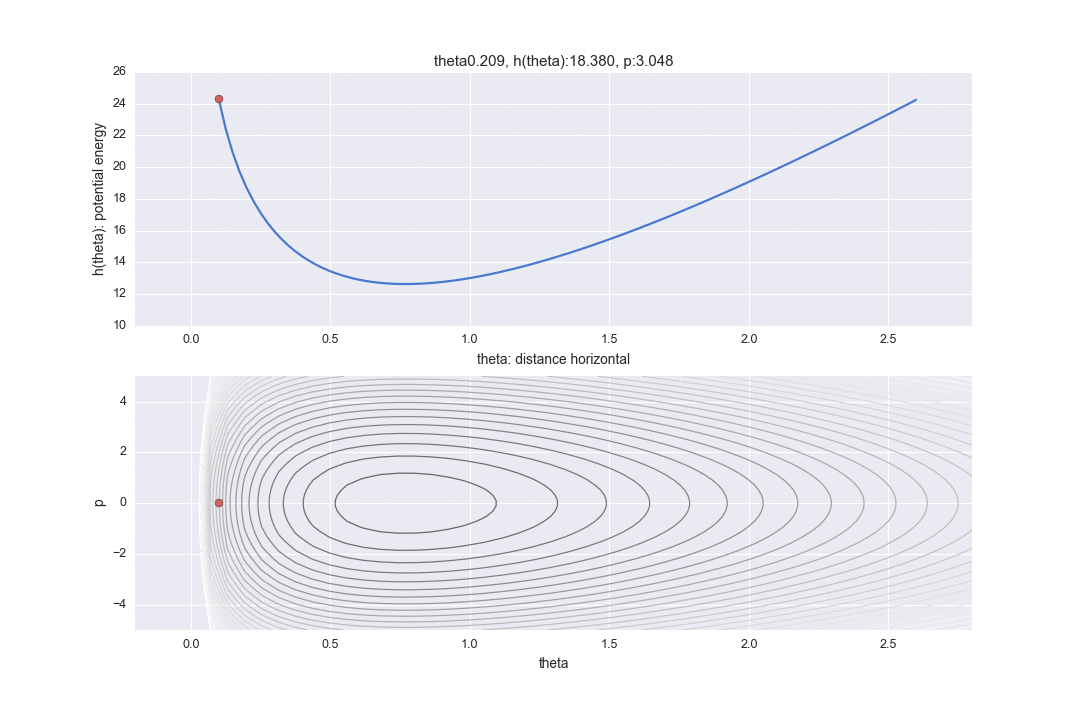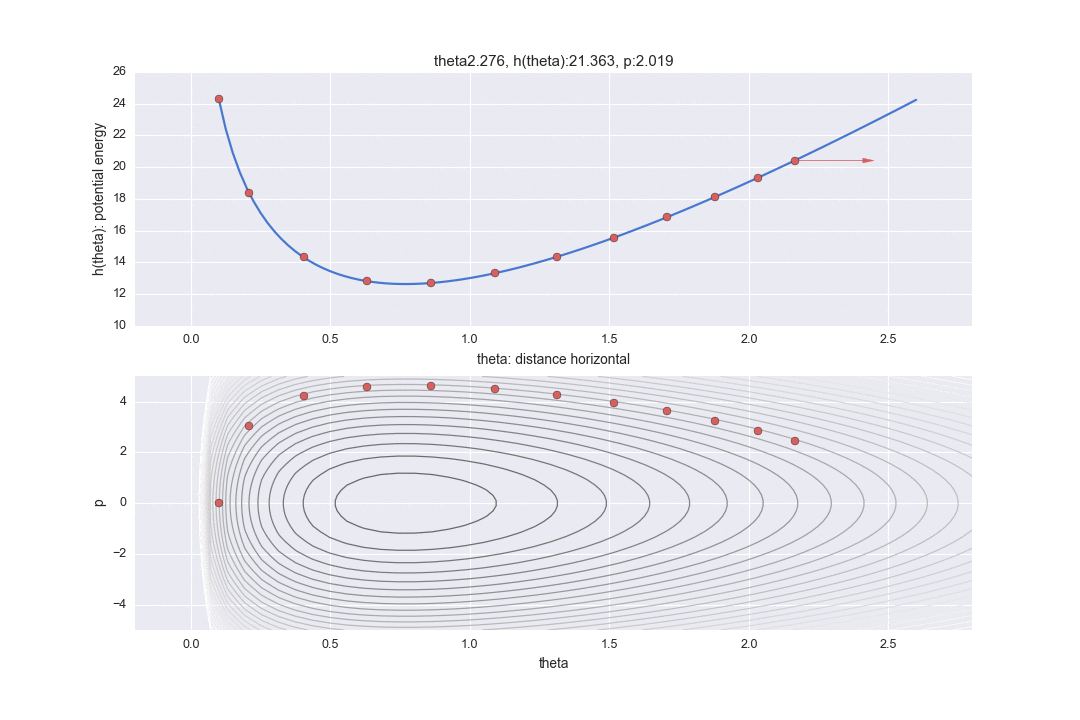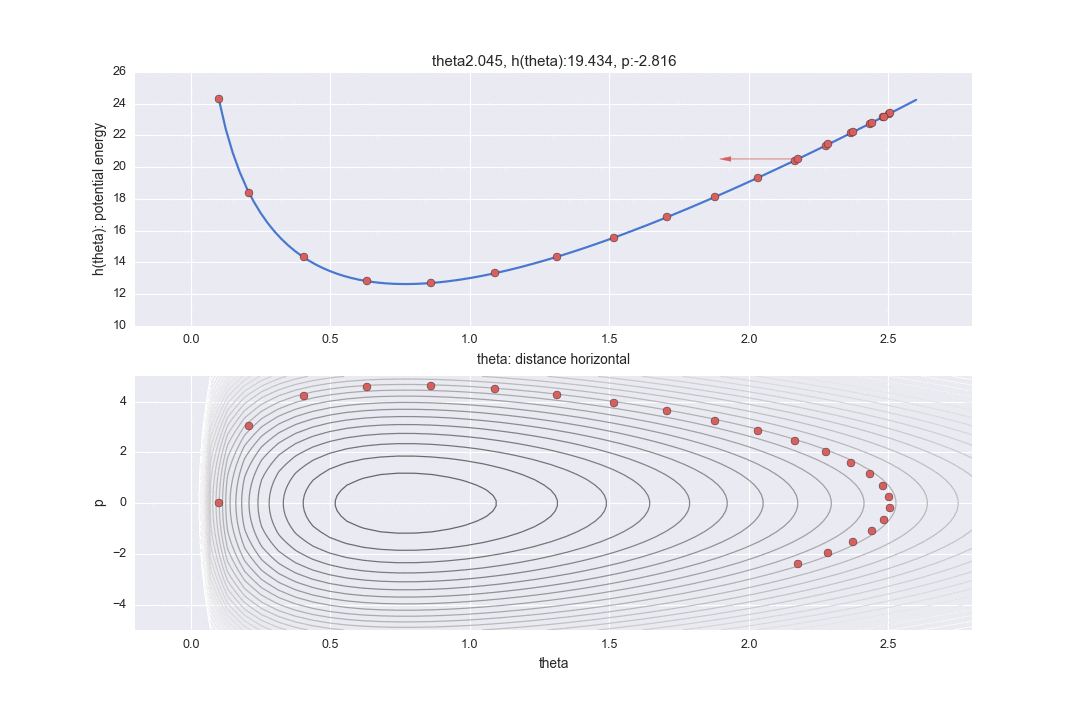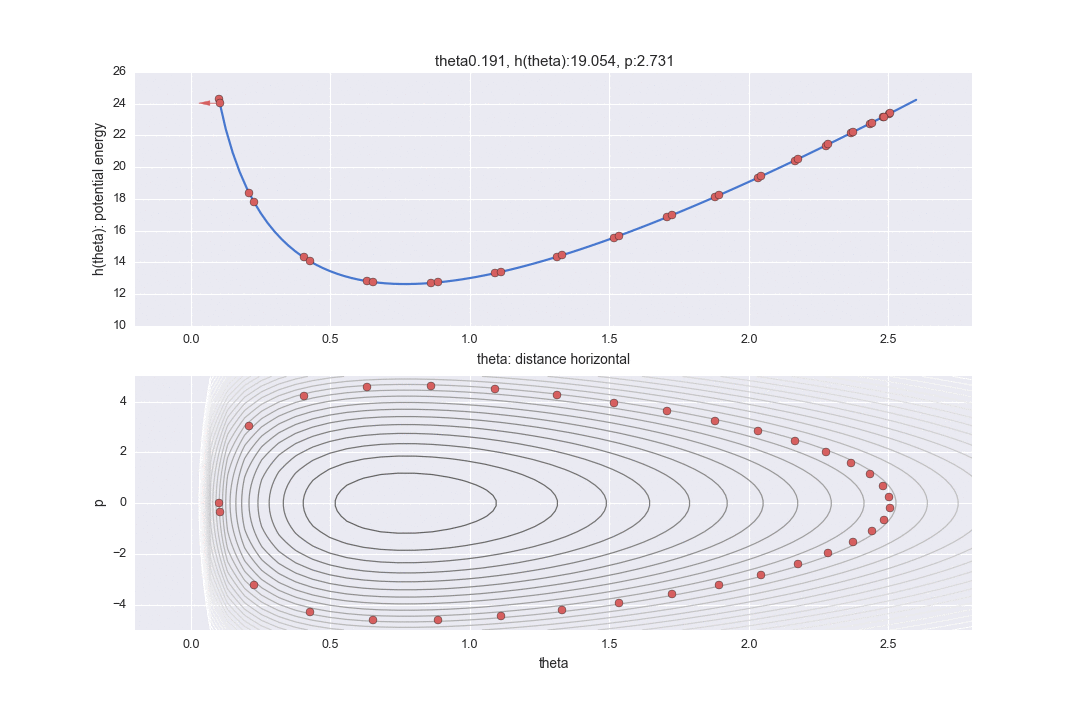
phase_space

De plus, le graphique de la partie inférieure est un graphique de ce qu'on appelle un espace des phases, avec l'axe horizontal représentant la distance horizontale $ \ theta $ et l'axe vertical représentant l'énergie cinétique $ p $. (Contrairement aux manuels, la figure est inversée verticalement et horizontalement pour aligner l'axe horizontal avec le graphique ci-dessus.) La ligne de contour montre la partie où l'hamiltonien est constant. Par conséquent, en partant du principe que l'hamiltonien est constant, il est montré dans deux méthodes d'affichage, la position horizontale correspondante et la vue que l'énergie cinétique est différente.

Méthode Leap Frog

Comme le montre la figure ci-dessus, la méthode Leapfrog est utilisée comme méthode de calcul numérique de l'hamiltonien afin qu'il se déplace à un certain endroit. Pour plus de détails sur la théorie, reportez-vous au livre, mais ici je publierai le code python. C'est une méthode pour réduire l'erreur due au calcul numérique en calculant la position à côté de $ p $ de moitié.

# function definitions

def h(theta):
    global lam, alpha
    return lam * theta - (alpha-1)*np.log(theta) 

def dh_dtheta(theta):
    global lam, alpha
    return lam - (alpha - 1)/theta

def hamiltonian(p, theta):
    return h(theta) + 0.5*p**2

vhamiltonian = np.vectorize(hamiltonian)  # vectorize

def leapfrog_nexthalf_p(p, theta, eps=0.01):
    """
    1/Calculer p après 2 étapes
    """
    return p - 0.5 * eps* dh_dtheta(theta)

def leapfrog_next_theta(p, theta, eps=0.01):
    """
Calculer θ après une étape
    """
    return theta + eps*p


def move_one_step(theta, p, eps=0.01, L=100, stlide=1):
    """
Exécuter une étape qui a déplacé L fois par la méthode de saut de grenouille
    """
    ret = []
    ret.append([1, p, theta, hamiltonian(p,theta)])
    for _ in range(L):
        p = leapfrog_nexthalf_p(p, theta, eps)
        theta = leapfrog_next_theta(p, theta, eps)
        p = leapfrog_nexthalf_p(p, theta, eps)
        ret.append([1, p, theta, hamiltonian(p,theta)])
    return ret[::stlide]

#Exécution de la méthode du saut à la grenouille
# initial param
theta = 0.1
p = 0
eps = 0.05
L = 96

result = move_one_step(theta, p, eps=eps, L=100, stlide=1)

Transition par la méthode du saut de grenouille et changement de moment p par distribution normale

La transition spécifiée par $ L $ est indiquée par la ligne pointillée dans le graphique ci-dessous. Il était difficile d'écrire toutes les trajectoires L, donc j'en ai sauté 12. Donc, en réalité, les points avancent plus finement.

De plus, une ligne rouge est affichée au milieu, ce qui signifie que l'énergie de position a été changée de manière aléatoire une fois après les temps de transition L. En particulier

p = rd.normal(loc=0,scale=scale_p)       # ------(*)

$ P $ est mis à jour avec un nombre aléatoire qui suit la distribution normale standard représentée par le code. (Je ne comprends pas pourquoi la ** distribution normale "standard" ** est utilisée ici. Il semble que ce n'est pas mal de pouvoir ajuster la variance en tant que paramètre ... Si quelqu'un sait, faites-le moi savoir ... À ce stade, la préservation de l'hamiltonien est interrompue et les lignes de contour de différentes valeurs hamiltoniennes sont à nouveau déplacées L fois. Un seul point juste avant que cette ligne rouge ne soit tracée est réellement utilisé pour l'échantillonnage, et les valeurs restantes sont simplement rejetées en tant que valeurs au milieu du calcul.

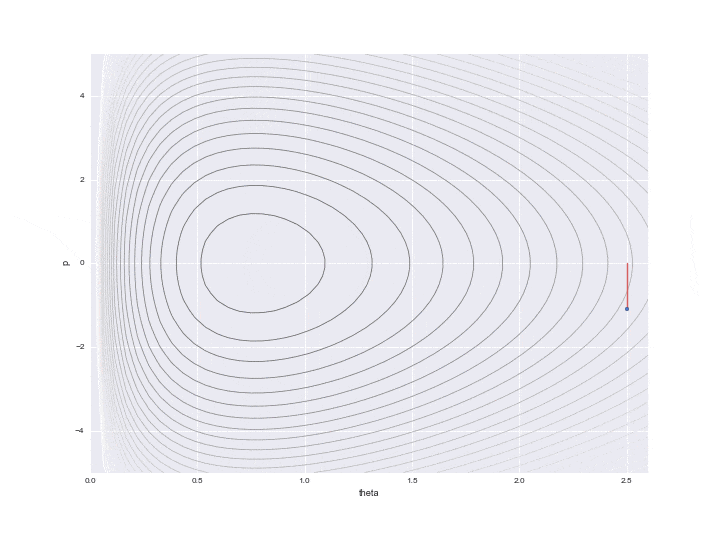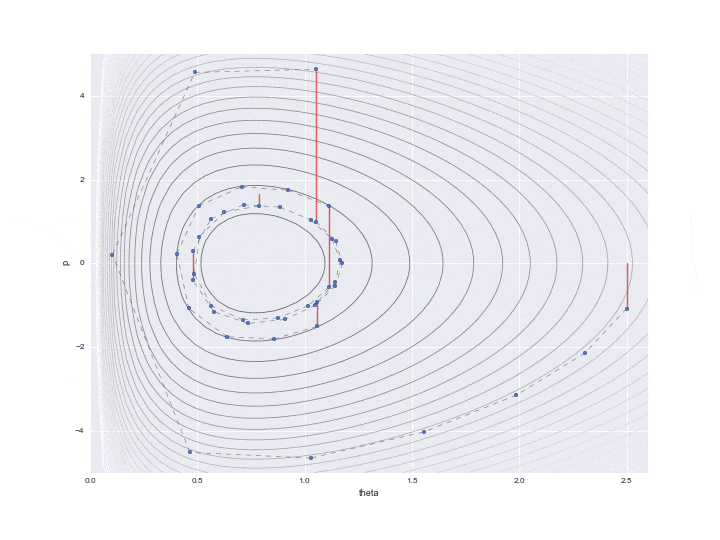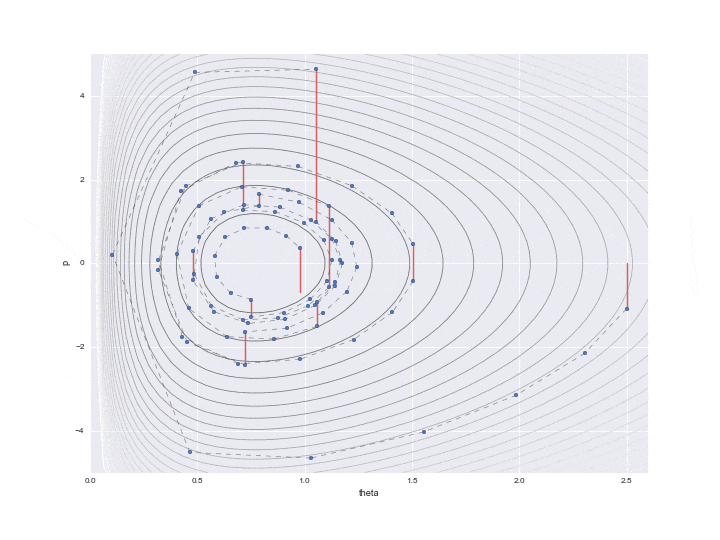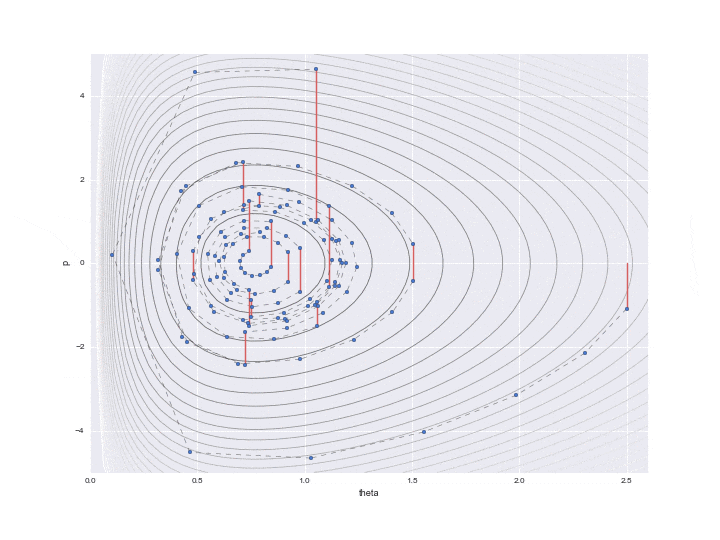
sampling

rd.seed(123)
theta = 2.5
eps = 0.01
T = 15

step = []
prev_p = 0

for tau in range(T):
    p = rd.normal(loc=0,scale=scale_p)       # ------(*)
    step.append([2, p, prev_p, 0])
    one_step = move_one_step(theta, p, eps=eps, L=96, stlide=12)
    theta = one_step[-1][2]
    step.extend(one_step)
    prev_p = one_step[-1][1]

    
print len(step)

def animate(nframe):
    global num_frame, n
    sys.stdout.write("{}, ".format(nframe))
    
    if step[n][0] == 1:
        plt.scatter(step[n][2], step[n][1], s=20, zorder=100)
        if step[n-1][0] == 1:
            plt.plot([step[n-1][2], step[n][2]],[step[n-1][1], step[n][1]], c="k", ls="--", lw=.8, alpha=0.5)
        
    else:
        theta = step[n+1][2]
        
        plt.plot([theta, theta], [step[n][2], step[n][1]], c="r")
        
    n += 1
    
    
num_frame = len(step)-1
n = 0
scale_p = 1
fig = plt.figure(figsize=(12,9))

xx = np.linspace(0.01, 2.6)
yy = np.linspace(-5,5)
X, Y = np.meshgrid(xx, yy)
Z = vhamiltonian(Y, X)
plt.contour(X, Y, Z, linewidths=1, cm=cm.rainbow, levels=np.linspace(0,40,40))

plt.ylabel("p")
plt.xlabel("theta")
plt.xlim(0,2.6)
plt.ylim(-5,5)

anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('hmc_sampling_detail.gif', writer='imagemagick', fps=5, dpi=60)

échantillonnage

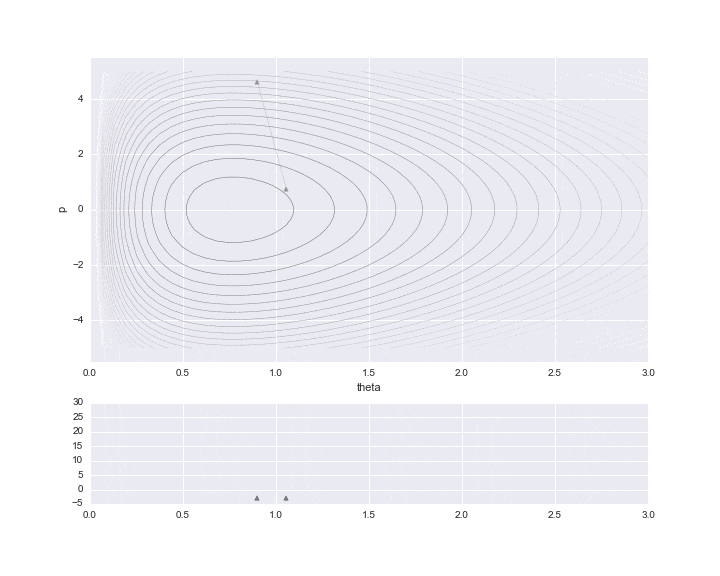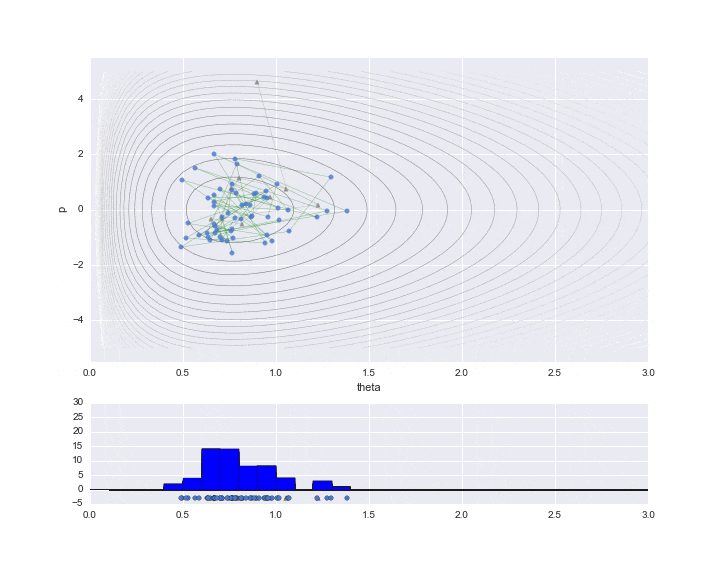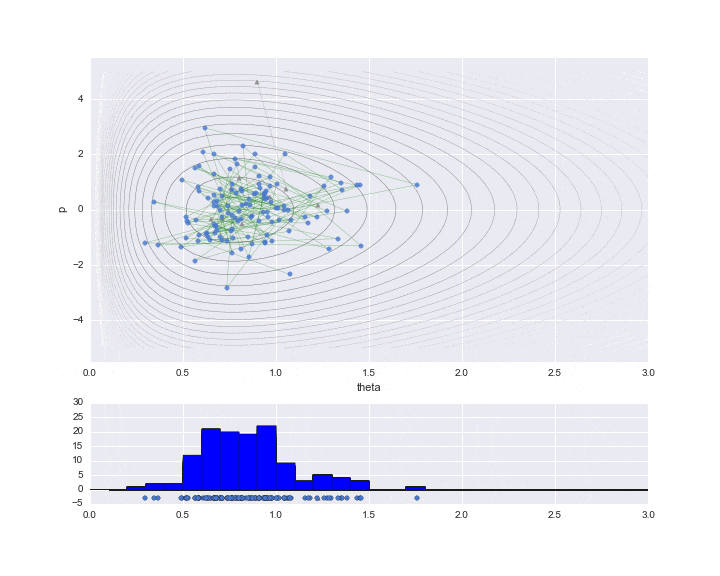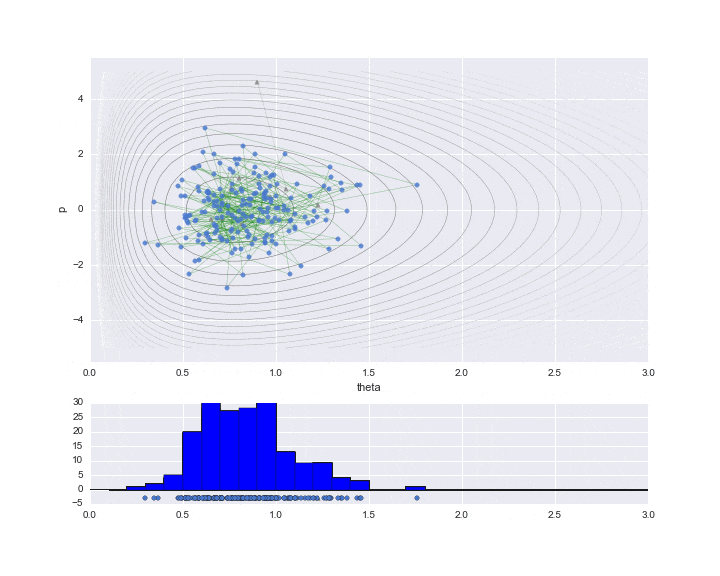
Vous trouverez ci-dessous le résultat du traçage uniquement des données réellement nécessaires.

Aussi,

r= \exp \left( H(\theta^{(t)}, p^{(t)}) - H(\theta^{(a)}, p^{(a)})\right)

Pour être le taux d'acceptation comme $ \ min (1, r) $

r = np.exp(prev_hamiltonian-H)       # -----(**)

Et «rd.uniform ()» sont comparés pour déterminer l'acceptation et la non-acceptation. Cependant, dans le cas de cet exemple, il n'a jamais été rejeté, donc tout est accepté. La période de rodage est réglée sur 10 et les valeurs échantillonnées sont indiquées par ▲ pendant cette période. Le graphique inférieur est un histogramme de la valeur de $ \ theta $ à estimer. Nous n'avons échantillonné qu'un peu moins de 200, mais nous pouvons voir qu'il s'agit d'un histogramme de la forme de distribution comme la distribution gamma déformée vers la droite.

hmc_simulation

# HMC simulation
rd.seed(71)
scale_p = 1

# initial param
theta = 2.5
p = rd.normal(loc=0,scale=scale_p)
eps = 0.01
L = 100
T = 10000
sim_result = []
prev_hamiltonian = hamiltonian(p,theta)
sim_result.append([ p, theta, prev_hamiltonian, True])
for t in range(T):
    prev_p = p
    prev_theta = theta
    prev_hamiltonian = hamiltonian(p,theta)
    for i in range(L):
        p = leapfrog_nexthalf_p(p, theta, eps=eps)
        theta = leapfrog_next_theta(p, theta, eps=eps)
        p = leapfrog_nexthalf_p(p, theta, eps=eps)

    H = hamiltonian(p,theta)
    r = np.exp(prev_hamiltonian-H)       # -----(**)
    if  r > 1:
        sim_result.append([ p, theta, hamiltonian(p,theta), True])
    elif r > 0 and rd.uniform() < r:
        sim_result.append([ p, theta, hamiltonian(p,theta), True])
    else:
        sim_result.append([ p, theta, hamiltonian(p,theta), False])
        theta = prev_theta
    
    p = rd.normal(loc=0,scale=scale_p)
    
sim_result = np.array(sim_result)
df = pd.DataFrame(sim_result, columns="p,theta,hamiltonian,accept".split(","))
#df
print "accept ratio: ", np.sum([df.accept == 1])/len(df)

L'acceptation est proche de 100%: sourire:

`out`


accept ratio:  0.999900009999

Voici le code qui a généré l'animation jusqu'à T = 200.

def animate(nframe):
    global num_frame, n
    sys.stdout.write("{}, ".format(nframe))
     
    ####Rangée supérieure#####
    if n < burn_in:
        marker = "^"
        color  = "gray"
        lc     = "gray"
    else:
        marker = "o"
        color  = "b"
        lc     = "green"

    if sim_result[i,3]  == 0:
        marker = "x"
        color  = "r"
        lc     = "gray"

    axs[0].scatter(sim_result[n,1], sim_result[n,0], s=20, marker=marker, 
                   zorder=100, alpha=0.8, color=color) #,

    if n > 1:
        axs[0].plot([sim_result[n-1,1], sim_result[n,1]],
                    [sim_result[n-1,0], sim_result[n,0]], c=lc, lw=0.5, alpha=0.4)

        
    ####Rangée inférieure#####
    axs[1].scatter(sim_result[n,1], -3, alpha=1, marker=marker, c=color)

    if n > burn_in:
        hist_data = pd.DataFrame(sim_result[burn_in:n], columns="p,theta,hamiltonian,accept".split(","))
        hist_data = hist_data[hist_data.accept ==1]
        hist_data.theta.hist(bins=np.linspace(0,3,31),ax=axs[1], color="blue",)
    ### ========================
    
    n += 1
    
burn_in = 10
num_frame = 200
n = 1
n_col = 1
n_row = 2

fig, _ = plt.subplots(n_row, n_col, sharex=False, figsize=(10,8)) 
gs = gridspec.GridSpec(n_row, n_col, height_ratios=[3,1])
axs = [plt.subplot(gs[i]) for i in range(n_row*n_col)]

xx = np.linspace(0.01, 3)
yy = np.linspace(-5,5)
X, Y = np.meshgrid(xx, yy)
Z = vhamiltonian(Y, X)
axs[0].contour(X, Y, Z, linewidths=0.5, cm=cm.rainbow, levels=np.linspace(0,40,40))
    
axs[0].set_ylabel("p")
axs[0].set_xlabel("theta")
axs[0].set_xlim(0,3)
axs[1].set_xlim(0,3)
axs[1].set_ylim(-5,30)
    
anim = ani.FuncAnimation(fig, animate, frames=int(num_frame), blit=True)
anim.save('hmc_simulation2.gif', writer='imagemagick', fps=4, dpi=72)

Échantillonnage à grande échelle

Jusqu'à ce qui précède, T a été défini sur une petite valeur de 200 pour l'animation, mais voici un tracé de tous les T = 10000. burn-in est spécifié comme 1000.

Un tracé de trace de $ \ theta $. La partie grise de la première moitié est la partie à brûler.

Voici un histogramme des résultats. Si vous le comparez à la distribution gamma de $ \ alpha = 11, \ lambda = 13 $, vous pouvez voir qu'ils sont presque les mêmes: grin:

en conclusion

Il a été dit que l'utilisation de la méthode hamiltonienne de Monte Carlo augmenterait le taux d'acceptation de l'échantillonnage, mais il a été constaté que le taux d'acceptation était certainement élevé (près de 100% cette fois): satisfait:

référence

"Statistiques de Bayes à partir des bases-Une introduction pratique à la méthode hamiltonienne de Monte Carlo-" (édité par Hideki Toyoda) https://www.asakura.co.jp/books/isbn/978-4-254-12212-1/

Code complet pour cet article https://github.com/matsuken92/Qiita_Contents/blob/master/Bayes_chap_05/HMC_Gamma-for_Publish.ipynb (Navigation recommandée sur PC, veuillez naviguer en mode bureau sur smartphone.)

Préférences pour générer des GIF animés à partir de Python sur Mac http://qiita.com/kenmatsu4/items/573ca0733b192d919d0e

Introduction aux statistiques bayésiennes à partir des bases http://stats-study.connpass.com/event/27129/ → Il s'agit d'une session d'étude pour ce livre que j'anime.