2. Analyse multivariée expliquée dans Python 7-3. Arbre de décision [arbre de retour]

• Un autre aspect de l'arbre de décision, ** l'arbre de régression ** avec la variable objectif sous forme de données numériques.
• Pour l '** arbre de classification ** dont la variable objectif est des données catégorielles, utilisez le ** DecisionTreeClassifier ** du module scikit-learn.tree, mais utilisez le ** DecisionTreeRegressor ** pour le modèle ** de l'arbre de régression **.

⑴ Bibliothèque d'importation

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

from sklearn.tree import DecisionTreeRegressor #Classe pour créer un modèle d'arbre de régression

⑵ Acquisition et lecture de données

from sklearn.datasets import load_boston
boston_dataset = load_boston()

• Pour les données, utilisez le «jeu de données sur les prix des logements à Boston» fourni avec scikit-learn.
• Il y a 13 caractéristiques et 506 échantillons liés à la situation du logement à Boston, une grande ville du nord-est des États-Unis.
• L'objectif de cet ensemble de données est de prédire les prix des maisons en utilisant des caractéristiques données.
• La cible est le prix de la maison avec le nom de variable MEDV (abréviation de valeur médiane), et les 13 quantités caractéristiques sont des variables explicatives pour prédire le prix de la maison.
• Cliquez ici pour plus de détails tels que le contenu des variables explicatives https://qiita.com/y_itoh/items/aaa2056aac0c270ba7d2

** Construisez un modèle d'arbre de régression qui prédit le prix d'une maison en utilisant les 13 variables explicatives qui caractérisent la maison. ** **

• Tout d'abord, convertissez 13 variables explicatives en un bloc de données.

#Stocker les variables explicatives dans DataFrame
boston = pd.DataFrame(boston_dataset.data, columns=boston_dataset.feature_names)

print(boston.head()) #Afficher les 5 premières lignes
print(boston.columns) #Afficher le nom de la colonne
print(boston.shape) #Vérifiez la forme

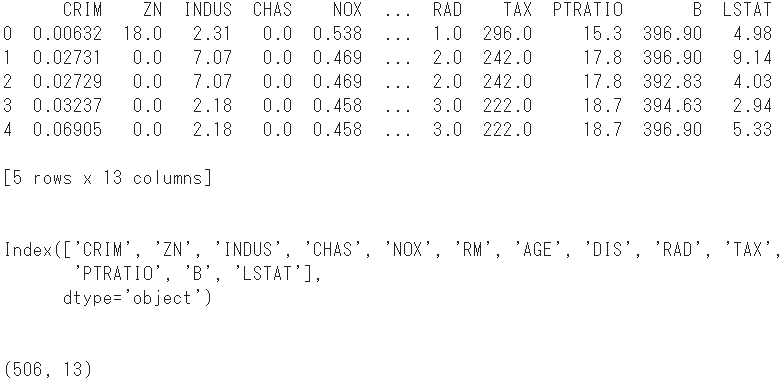
• Ajoutez-y la variable objectif comme nom de colonne MEDV

#Ajouter une variable d'objectif
boston['MEDV'] = boston_dataset.target

print(boston.head()) #Afficher les 5 premières lignes
print(boston.shape) #Reconfirmez la forme

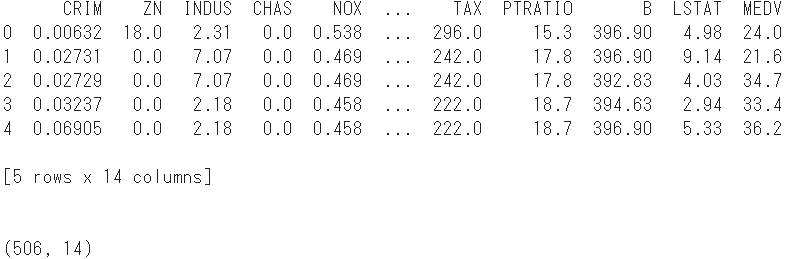
• Le nombre d'échantillons est de 14 colonnes en ajoutant la variable objective aux variables explicatives de 506 et 13.
• Divisez au hasard cet ensemble de données en deux groupes, un ensemble de données d'entraînement et un ensemble de données de test.

⑶ Division des données

#Convertir l'ensemble de données en tableau Numpy
array = boston.values

#Diviser en variables explicatives et variables objectives
X = array[:,0:13]
Y = array[:,13]

• 70% des données sont utilisées comme données d'entraînement et les 30% restants sont utilisés comme données de test.

#Importer un module qui divise les données
from sklearn.model_selection import train_test_split

#Diviser les données
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=1234)

⑷ Construction d'un modèle d'arbre de régression

• Comme pour l'arbre de classification, la méthode fit est entraînée en passant les tableaux X et Y, mais dans ce cas Y est de type numérique.
• L'option optionnelle max_leaf_nodes spécifie la croissance de l'arbre. Ici, le nombre maximum de nœuds feuilles est de 20.

#Instanciation du modèle
reg = DecisionTreeRegressor(max_leaf_nodes = 20)

#Génération de modèles par apprentissage
model = reg.fit(X_train, Y_train)
print(model)

⑸ Évaluation du modèle d'arbre de régression

• Le modèle d'arbre de régression obtenu est testé dans deux directions: la validité de la prédiction (➀) et la polyvalence du modèle lui-même (➁).
• Premièrement, afin de confirmer la validité de la prédiction, on est sélectionné au hasard parmi 506 échantillons, et le prix prédit à partir de la quantité caractéristique est comparé au prix réellement observé.

➀ Confirmer la validité de la prédiction

• Récupérez aléatoirement un seul identifiant de l'ensemble de données d'origine X.

#Importer le module de nombres pseudo aléatoires standard de Python
import random
random.seed(1)

#Sélectionnez un identifiant au hasard
id = random.randrange(0, X.shape[0], 1)
print(id)

#Extraire l'échantillon pertinent de l'ensemble de données d'origine
x = X[id]
x = x.reshape(1,13)

#Prédire les prix des logements à partir de variables explicatives
YHat = model.predict(x)

#Convertir la variable explicative de l'id en DataFrame
df = pd.DataFrame(x, columns = boston_dataset.feature_names)
#Valeur prédite ajoutée y
df["Predicted Price"] = YHat

• Obtenez les prix immobiliers réellement observés et comparez-les.

boston.iloc[id]

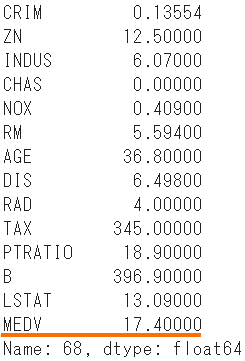
• Le prix attendu est de 20,45, comparé au prix réel de 17,40.
• La prochaine vérification est de savoir dans quelle mesure la valeur prédite du modèle peut expliquer la quantité d'informations de la valeur observée.

➁ Vérifiez le coefficient de décision comme un indice de polyvalence

• Le coefficient de décision $ R ^ 2 $ est un indice qui exprime le pouvoir explicatif de la valeur prédite $ \ hat {y} $ pour la valeur observée $ y $ dans l'analyse de régression, et est également appelé taux de cotisation.
• Prend une valeur de 0 à 1, et plus $ R ^ 2 $ est proche de 1, plus le modèle est valide.

#Importez la fonction pour calculer le coefficient de décision
from sklearn.metrics import r2_score

• Passez la variable explicative pour le test (X_test) au modèle pour calculer la valeur prédite.

YHat = model.predict(X_test)

• Passez ces valeurs prédites et la variable objectif pour le test (Y_test) pour calculer le facteur de décision.

r2 = r2_score(Y_test, YHat)
print("R^2 = ", r2)

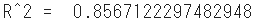
• L'ajustement du modèle dans les données de test est de 0,86, ce qui est un bon résultat.

⑹ Visualisation du modèle d'arbre de régression

#Importer le module d'arborescence sklearn
from sklearn import tree

#Module pour afficher des images dans Notebook
from IPython.display import Image

#Module de visualisation du modèle d'arbre de décision
import pydotplus

#Convertir le modèle d'arbre de décision en données DOT
dot_data = tree.export_graphviz(model,
                                out_file = None,
                                feature_names = boston_dataset.feature_names,
                                class_names = 'MEDV',
                                filled = True)

#Dessinez un diagramme
graph = pydotplus.graph_from_dot_data(dot_data)  

#Afficher le diagramme
Image(graph.create_png())

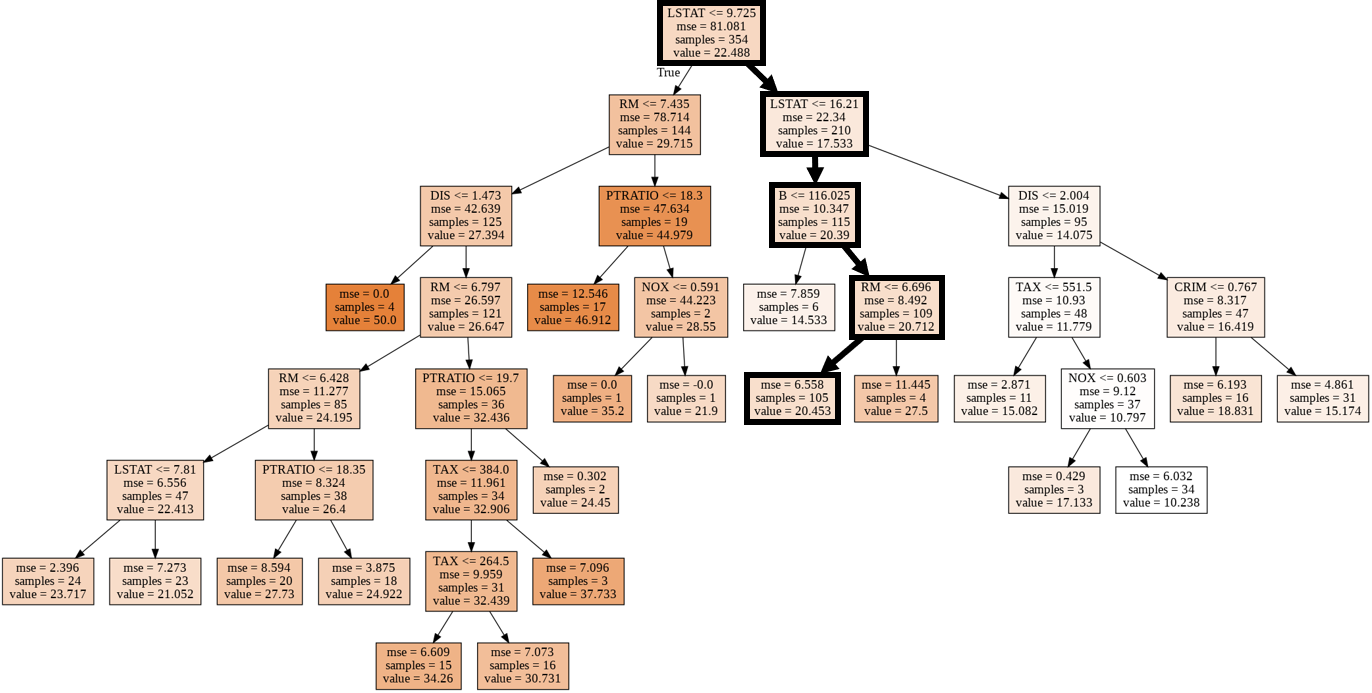
• Le parcours de l'échantillon extrait au hasard (ID: 68) est indiqué par une ligne épaisse.
• En passant, la quantité d'entités "LSTAT" du nœud parent et du nœud enfant de la première couche est une abréviation de "statut inférieur" et signifie le rapport de la classe inférieure à la population.