[PYTHON] Chainer et deep learning appris par approximation de fonction
Apprenons à chainer à travers le thème de l'apprentissage de la fonction $ y = e ^ x $ par le soi-disant apprentissage profond. Ce qui suit est confirmé avec le chainer 1.6.2.1.
Le même contenu est placé au format notebook Jupyter ici, donc si vous voulez le vérifier en vous déplaçant, veuillez vous y référer.
Tout d'abord, importez les modules requis.
import numpy as np
import chainer
from chainer import cuda, Function, gradient_check, Variable, optimizers, serializers, utils
from chainer import Link, Chain, ChainList
import chainer.functions as F
import chainer.links as L
from matplotlib import pyplot as plt
%matplotlib inline
Création de données enseignants
Tout d'abord, créez une fonction qui génère des données sur l'enseignant. Cette fois, $ e ^ x $ est la valeur attendue de la fraction flottante $ x $ de 0 à 1,0.
Nous utilisons une technique appelée apprentissage par lots, mais il est pratique d'avoir une fonction qui renvoie un ensemble de questions et réponses $ n $.
def get_batch(n):
x = np.random.random(n)
y = np.exp(x)
return x,y
print get_batch(2)
(array([ 0.25425583, 0.87356596]), array([ 1.28950165, 2.39543768]))
Conception de réseau neuronal
Ensuite, concevez le réseau neuronal.
Puisque $ y = e ^ x $ est une fonction non linéaire, l'approximation avec seulement une fonction linéaire n'est pas assez précise. Lorsque l'entrée est $ x $, quelque chose comme $ y = Wx + b $ est appelé une fonction linéaire. $ W $ est appelé un poids et $ b $ est appelé un biais, qui ne sont que des matrices. En d'autres termes, c'est une ligne droite (comme).
D'ailleurs, pour cette opération linéaire, il semble qu'on puisse l'appeler un réseau de neurones simplement en ajoutant une couche d'activation par une fonction non linéaire. Une version multicouche de ceci est un réseau neuronal profond, une fonction non linéaire utilisée dans ce que l'on appelle l'apprentissage profond. Je ne sais pas à quelle profondeur cela devrait être appelé deep, mais cette fois, je vais essayer environ 3 étapes.
Dans un problème de classification général, une fonction non linéaire appelée relu est utilisée très souvent, mais dans le cas de relu, le différentiel disparaît, donc leaky_relu est utilisé cette fois (dans ce cas, relu n'a pas convergé). .. leaky_relu est une fonction simple qui multiplie 0,2 si l'entrée est négative.
En optimisant les paramètres $ W et b $ de chaque couche linéaire, nous essaierons d'exprimer une fonction qui correspond à $ y = e ^ x $.
Alors, configurons le réseau neuronal comme suit. L1, L2 et L3 sont respectivement des fonctions linéaires. Après avoir augmenté les dimensions de la couche intermédiaire $ h1 et h2 $ à 16 et 32, elles sont finalement ramenées à une dimension.

Dans ce qui suit, les paramètres $ W, b $ de $ L_n $ sont exprimés comme $ W_n, b_n $.
Le fait que la couche intermédiaire (couche cachée) $ h1, h2 $ puisse avoir plusieurs canaux (c'est-à-dire que la matrice de paramètres $ W_n, b_n $ est énorme) montre la puissance expressive du réseau. S'il n'y a pas d'élément non linéaire au milieu
\begin{eqnarray*}
h_3 &=& W_3 (W_2(W_1x+b_1)+b_2)+b_3 \\
&=& W_3 W_2 W_1 x + W_3W_2b_1 + W_3b_2 + b_3 \\
&=& W x + b
\end{eqnarray*}
Ce sera. $ W = W_3 W_2 W_1, b = W_3 W_2b_1 + W_3b_2 + b_3 $, mais quelle que soit la taille de la matrice telle que $ W_1, W_2, W_3 $, les paramètres $ W et b $ de la fonction composite sont tous les deux. Ce sera un scalaire. Le fait que $ x, W, b $ soient tous des scalaires signifie que $ y = Wx + b $ est une ligne droite qui ne peut changer que la pente et la section, et l'ajuster à $ e ^ x $. C'est impossible. Cependant, tous les paramètres de $ W_1, W_2, W_3 $ seront vivants simplement en insérant un élément non linéaire. C'est la raison pour laquelle j'ai mentionné au début, "Si vous avez un élément non linéaire, vous pouvez l'appeler un réseau neuronal."
Implémentation du réseau neuronal
Écrivez ceci avec le chainer.
Dans le chainer, les fonctions avec des paramètres à optimiser sont appelées L (lien), et les fonctions sans paramètres sont appelées F (fonction) pour les distinguer. Il semble que ce domaine soit un concept introduit à partir de la version 1.5 environ, et je vois souvent des tutoriels qui écrivent des liens avec des fonctions. Les liens sont définis en commençant par des majuscules comme L.Linear (taille d'entrée, taille de sortie), et les fonctions sont définies en commençant par des minuscules comme F.linear (x, W, b). Les versions plus anciennes semblaient utiliser des fonctions basées sur les majuscules, notamment F.Linear (), L.Linear () et F.linear (). Les deux premiers sont des fonctions équivalentes et paramétrées, et le dernier est juste une fonction qui donne des paramètres. J'étais assez confus avant de comprendre cela.
L'histoire était un peu décalée. Ensuite, passez une collection de liens pour créer une classe appelée chaîne. Si vous n'êtes pas familiarisé avec l'écriture de classes Python, vous serez ennuyé, mais tout ce dont vous avez besoin est \ _ \ _ init \ _ \ _ () pour définir la liste de liens et une fonction pour renvoyer le graphique calculé à la sortie. Ici, nous retournerons la perte comme \ _ \ _ cal \ _ \ _ (). La fonction définie par \ _ \ _ call \ _ \ _ () est
m=MyChain()
loss=m(x,t)
Vous pouvez l'appeler comme ça.
Le fait est que la fonction incluant le paramètre est séparée en \ _ \ _ init \ _ \ _ (), et les autres sont séparées afin qu'elles puissent être utilisées dans \ _ \ _ call () \ _ \ _ et d'autres méthodes. L.Linear () est beaucoup plus facile à écrire que TensorFlow car il vous suffit de transmettre le nombre de canaux d'entrée et de sortie comme paramètres.
class MyChain(Chain):
def __init__(self):
super(MyChain, self).__init__(
l1=L.Linear(1, 16), #1 canal d'entrée, 16 canaux de sortie
l2=L.Linear(16, 32),
l3=L.Linear(32, 1),
)
def __call__(self,x,t):
#Renvoie la différence entre la sortie réseau lorsque x est entré et la réponse t.
#Cette fois, nous utiliserons l'erreur quadratique moyenne.
return F.mean_squared_error(self.predict(x),t)
def predict(self,x):
#Renvoie la sortie réseau lorsque x est entré.
h1 = F.leaky_relu(self.l1(x))
h2 = F.leaky_relu(self.l2(h1))
h3 = F.leaky_relu(self.l3(h2))
return h3
def get(self,x):
#Il s'agit d'une fonction pratique qui renvoie la sortie sous forme de nombre réel après avoir entré x comme nombre réel.
# numpy.C'est un peu déroutant car il passe par ndarray et Variable.
return self.predict(Variable(np.array([x]).astype(np.float32).reshape(1,1))).data[0][0]
Créez une instance de ce modèle et configurez l'optimiseur pour optimiser les paramètres en fonction de votre stratégie spécifique. Cette fois, j'utiliserai quelque chose appelé Adam ().
model = MyChain()
optimizer = optimizers.Adam()
optimizer.setup(model)
Apprentissage
Enfin, nous allons tourner la boucle d'apprentissage.
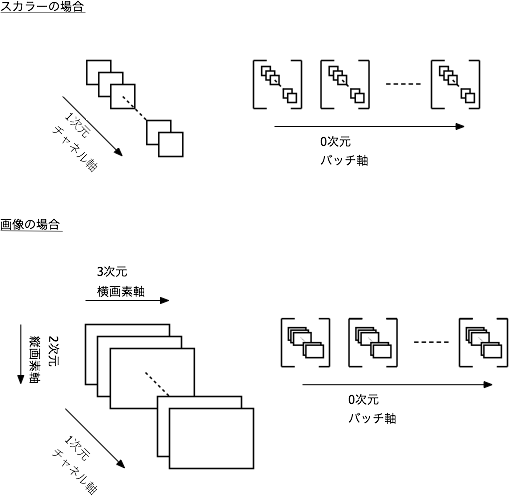
En tant que méthode de chaînage, un tableau multidimensionnel (tenseur) de np.float32 avec une structure dimensionnelle (axe batch, axe de données 1, (axe de données 2), ..) est converti en une classe Variable et échangé. Utilisez la méthode data pour récupérer le nombre réel de la classe Variable. ... Je ne comprends pas du tout quand je l'écris.
Un lot est un échantillon de certains des données de l'enseignant. Est-il plus facile de comprendre le nombre de lots comme le nombre d'échantillons? Les paramètres sont toujours mis à jour pour plusieurs numéros d'échantillons, mais un tableau multidimensionnel (tenseur) est géré, dans lequel une dimension appelée le nombre de canaux de données est ajoutée, puis les dimensions requises pour la représentation des données sont ajoutées. Ce sera.
Dans ce cas, les données d'entrée sont unidimensionnelles, donc (Axe des lots, axe des données) C'est bien, mais les données composées de canaux RGB3 d'images 2D sont (Axe du lot, axe du canal = axe des couleurs, axe vertical, axe horizontal) Passez comme. C'est difficile à comprendre à moins de s'y habituer. J'imagine la figure ci-dessous.
Mises à jour d'apprentissage
- Initialisation de la différenciation
- Propagation en avant (en suivant le réseau en avant pour calculer la sortie, dans ce cas modèle (x \ _, t \ _))
- Propagation vers l'arrière (traçage du réseau en arrière pour calculer le différentiel des paramètres)
- Mise à jour de l'optimiseur (mise à jour des paramètres en utilisant la différenciation)
Est une série de flux. optimizer.update (model) le fera immédiatement, mais je veux souvent voir la progression de forward, donc j'écris souvent tout comme suit.
losses =[]
for i in range(10000):
x,y = get_batch(100)
x_ = Variable(x.astype(np.float32).reshape(100,1))
t_ = Variable(y.astype(np.float32).reshape(100,1))
model.zerograds()
loss=model(x_,t_)
loss.backward()
optimizer.update()
losses.append(loss.data)
plt.plot(losses)
plt.yscale('log')

L'axe horizontal est le nombre de boucles et l'axe vertical est le tracé logarithmique de la perte. Cela a été réduit à un bon sentiment.
Vérifiez le résultat
Vérifions maintenant la sortie du modèle terminé. Si vous entrez 0,2, obtiendrez-vous une valeur proche de exp (0,2)?
print model.get(0.2)
print np.exp(0.2)
1.22299
1.22140275816
Ça m'a l'air bien. Alors, dans quelle mesure la fonction peut-elle s'intégrer dans la plage de 0 à 1?
x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=model.predict(Variable(x.astype(np.float32).reshape(100,1))).data
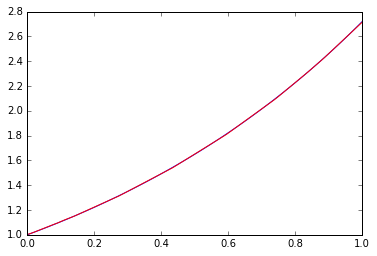
_=plt.plot(x, p,"r")

Le bleu est la bonne réponse et le rouge est le résultat de l'apprentissage.
se sentir bien. Cette performance d'ajustement ne peut pas être obtenue avec la fonction linéaire seule. Il est intéressant de changer la profondeur, la largeur (nombre de dimensions), etc. du filet, mais comme on le dit souvent, on peut confirmer que les éléments non linéaires et la profondeur sont plus importants que la largeur.
Observation du modèle de résultats d'entraînement
Voyons maintenant de quel type de coefficient le modèle après l'entraînement des résultats est constitué. Par exemple, le poids $ W $ de la première couche l1 est accessible comme suit.
model.l1.W.data
array([[ 0.31513408],
[ 0.75111604],
[ 0.48637491],
[-1.34837043],
[ 0.0388922 ],
[-1.29884255],
[-0.49960354],
[ 0.35992688],
[ 0.25262424],
[-2.14205575],
[ 0.83558381],
[-0.61535668],
[ 2.15679836],
[-0.17658199],
[-1.36228967],
[-0.5751065 ]], dtype=float32)
Vous pouvez l'utiliser pour créer une fonction qui renvoie la même sortie avec numpy, par exemple:
def leaky_relu(x):
#Parcourez ndarray une fois pour effectuer une opération élément par élément
m = np.array((x<0))
x = np.array(x)
return np.matrix((x*0.2)*m + x*(~m))
def pseudo_exp(x):
x = np.matrix(x)
W1 = np.matrix(model.l1.W.data)
b1 = np.matrix(model.l1.b.data)
W2 = np.matrix(model.l2.W.data)
b2 = np.matrix(model.l2.b.data)
W3 = np.matrix(model.l3.W.data)
b3 = np.matrix(model.l3.b.data)
h1 = leaky_relu(W1*x+b1.T)
h2 = leaky_relu(W2*h1+b2.T)
y = leaky_relu(W3*h2+b3.T)
return y
print pseudo_exp(0.2)
print np.exp(0.2)
[[ 1.22299392]]
1.22140275816
x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=pseudo_exp(x.T)
_=plt.plot(x, p.T,"r")
Si vous notez les valeurs de coefficient telles que model.l1.W.data telles quelles, vous pouvez écrire complètement le modèle de résultat de la formation avec juste numpy. La conversion vers un langage tel que C ou Go ne devrait pas non plus être difficile. Eh bien, chainer et numpy sont assez rapides pour plus de commodité, donc je ne pense pas qu'il soit nécessaire de convertir dans une autre langue juste pour la vitesse, mais si vous voulez juste utiliser un modèle post-apprentissage, ce genre d'approche Dans certains cas, il peut être utile de convertir dans un format qui ne dépend pas d'une bibliothèque d'apprentissage automatique telle que chainer.
Observation et sauvegarde des progrès
Maintenant, lorsque vous essayez de faire des erreurs sur Jupyter, vous voudrez voir les progrès. Si vous écrivez comme ci-dessous, le tracé de progression sera mis à jour. Cela dépend de la vitesse de convergence, mais j'essaye de mettre à jour l'affichage une fois toutes les 10 fois.
De plus, l'épargne est importante. Économisez une fois toutes les 100 fois.
losses =[]
from IPython import display
model = MyChain()
optimizer = optimizers.Adam()
optimizer.setup(model)
plt.hold(False)
for i in range(500):
x,y = get_batch(100)
x_ = Variable(x.astype(np.float32).reshape(100,1))
t_ = Variable(y.astype(np.float32).reshape(100,1))
model.zerograds()
loss=model(x_,t_)
loss.backward()
optimizer.update()
losses.append(loss.data)
if i%10==0:
plt.plot(losses,"b")
plt.yscale('log')
display.clear_output(wait=True)
display.display(plt.gcf())
if i%100==0:
serializers.save_npz('my.model', model)
display.clear_output(wait=True)

Regardons la sortie en utilisant le modèle enregistré.
serializers.load_npz('my.model',model)
model.get(0.2)
1.1877015
Qu'est-ce que la rétro-propagation?
Maintenant, entrons dans un petit principe. Qu'est-ce que cela signifie que les paramètres sont optimisés par rétro-propagation en premier lieu?
Par souci de simplicité, une fois que le réseau est retourné à une fonction linéaire ($ y = Wx + b $, $ W, b $ est juste une expression linéaire appelée scalaire), et l'optimiseur est renvoyé à un algorithme simple appelé SGD. Faites un seul lot.
Les valeurs initiales de $ W et b $, mais par défaut dans chainer, $ W $ est choisi comme nombre aléatoire et $ b $ est choisi comme $ 0 $. Ici, par souci de clarté, les valeurs initiales sont $ W = 0 et b = 0 $.
def get_batch(n):
x=np.random.random(n)
y= np.exp(x)
return x,y
class LinearChain(Chain):
def __init__(self):
super(LinearChain, self).__init__(
l1=L.Linear(1, 1,initialW=0.0),
)
def __call__(self,x,t):
return F.mean_squared_error(self.predict(x),t)
def predict(self,x):
return self.l1(x)
def get(self,x):
return self.predict(Variable(np.array([x]).astype(np.float32).reshape(1,1))).data[0][0]
Pour la fonction linéaire $ y = Wx + b $, l'erreur carrée de $ E = (y-t) ^ 2 $ est définie comme la fonction d'erreur.
Les paramètres $ W $ et $ b $ sont mis à jour afin de rapprocher cette erreur carrée de 0, et le sens de mise à jour est défini par la différenciation partielle de l'erreur $ E $ par chaque paramètre. En d'autres termes
\varDelta W = \frac{\partial E}{\partial W},\quad
\varDelta b = \frac{\partial E}{\partial b}
est. Cette valeur est appelée la différenciation des paramètres. Élargir cette formule
\begin{eqnarray*}
\varDelta W &=& \frac{\partial E}{\partial y} \frac{\partial y}{\partial W} &=& 2 \left(y-t \right) x \\
\varDelta b &=& \frac{\partial E}{\partial y} \frac{\partial y}{\partial b} &=& 2 \left( y-t \right) \\
\end{eqnarray*}
Ce sera. En transformant de cette manière, la différenciation du paramètre peut être exprimée par la différence de l'erreur, $ y-t $, et de l'entrée connue $ x $. Dans le processus de calcul, la différence de l'erreur qui est en aval renvoie à la différence des paramètres de l'expression qui est en amont, elle est donc appelée propagation en retour. $ t et x $ sont connus, mais $ y $ ne peut être obtenu qu'en calculant la propagation avant, ou $ Wx + b $. Ainsi, si vous effectuez le calcul de la propagation avant, puis de la propagation arrière, vous pouvez obtenir la différence entre les paramètres.
Cela ressemble à ceci sur la figure.

Mettez à jour $ W, b $ en utilisant $ \ varDelta W, \ varDelta b $ calculé de cette manière. SGD met simplement à jour les paramètres en multipliant la pente par un taux d'apprentissage constant $ \ alpha $. En d'autres termes
W \leftarrow W-\alpha \varDelta W , \quad b \leftarrow b-\alpha\varDelta b
Il sera mis à jour comme ça. La valeur par défaut du chainer est $ \ alpha = 0,01 $.
Vérifions ce mouvement.
model2 = LinearChain()
optimizer2 = optimizers.SGD()
optimizer2.setup(model2)
losses=[]
trace=[]
def scalar(v):
#Renvoie Valiable à la valeur scalaire
return v.data.ravel()[0]
for i in range(5):
x,y = get_batch(1)
x_ = Variable(x.astype(np.float32).reshape(1,1))
t_ = Variable(y.astype(np.float32).reshape(1,1))
model2.zerograds()
loss=model2(x_,t_)
loss.backward(retain_grad=True)
y = scalar(model2.predict(x_))
t=scalar(t_)
x=scalar(x_)
W=scalar(model2.l1.W)
b=scalar(model2.l1.b)
#Delta calculé manuellement_W,delta_b
dW_hand = 2*((y-t)*x)
db_hand = 2*((y-t))
#Delta calculé par le chainer_W, delta_b
dW=model2.l1.W.grad.ravel()[0]
db=model2.l1.b.grad.ravel()[0]
print "====== step %d ======" % i
print "W,b \t\t\t\t%2.8f, %2.8f" % (W,b)
print "2(y-t)x,2(y-t)\t\t%2.8f, %2.8f" % (2*((y-t)*x), 2*((y-t)))
print "⊿W,⊿b\t\t\t\t%2.8f, %2.8f" % (dW,db) #delta émis par le chainer_W, delta_b
print "W-α⊿W,b-α⊿b \t\t%2.8f, %2.8f" % (W-0.01*dW,b-0.01*db)
optimizer2.update()
====== step 0 ======
W,b 0.00000000, 0.00000000
2(y-t)x,2(y-t) -3.58069563, -4.46209097
⊿W,⊿b -3.58069563, -4.46209097
W-α⊿W,b-α⊿b 0.03580696, 0.04462091
====== step 1 ======
W,b 0.03580695, 0.04462091
2(y-t)x,2(y-t) -0.08072093, -1.99062216
⊿W,⊿b -0.08072093, -1.99062216
W-α⊿W,b-α⊿b 0.03661416, 0.06452713
====== step 2 ======
W,b 0.03661416, 0.06452713
2(y-t)x,2(y-t) -1.16285205, -2.84911036
⊿W,⊿b -1.16285205, -2.84911036
W-α⊿W,b-α⊿b 0.04824269, 0.09301824
====== step 3 ======
W,b 0.04824268, 0.09301823
2(y-t)x,2(y-t) -0.44180280, -2.23253369
⊿W,⊿b -0.44180280, -2.23253369
W-α⊿W,b-α⊿b 0.05266071, 0.11534357
====== step 4 ======
W,b 0.05266071, 0.11534357
2(y-t)x,2(y-t) -1.07976472, -2.70742726
⊿W,⊿b -1.07976472, -2.70742726
W-α⊿W,b-α⊿b 0.06345836, 0.14241784
Les deux points suivants peuvent être confirmés.
--Chainer grad renvoie la même valeur que le calcul manuel de $ 2 (y-t) x, 2 (y-t) $ --SGD met à jour $ W et b $ de 0,01 grad
Si vous regardez la source linéaire de chainer, elle est écrite de manière à pouvoir gérer plusieurs entrées et sorties. C'est un peu difficile à comprendre parce que c'est le cas, mais forward () est sorti comme $ Wx + b $, et backward () est sorti comme différentiel de $ W $ en multipliant le différentiel plus tard grad_outputs par $ x $. Vous pouvez voir qu'il est décrit. La sortie de backward () renvoie toutes les différentielles de $ x, W, b $.
De plus, si vous regardez la Source SGD, grad aura lr = 0.01 lorsque update () sera appelé. (lr est une abréviation pour le taux d'apprentissage) est multiplié et renvoyé en tant que paramètre.
Voyons maintenant comment la mise à jour aboutit à approcher la valeur optimale.
import matplotlib.path as mpath
import matplotlib.patches as patches
#Dessiner les contours de Ross
psize=40
W=np.linspace(-1,3,psize)
B=np.linspace(-1,3,psize)
Wm, Bm = np.meshgrid(W, B)
Z=np.zeros((psize,psize))
for w in range(psize):
for b in range(psize):
Z[b,w]=0.0
for x in np.linspace(0,1,10):
Z[b,w] += (W[w]*x+B[b]-np.exp(x))**2
plt.contourf(Wm,Bm, Z, 100,vmax=80,vmin=0)
plt.colorbar()
plt.hold(True)
model2 = LinearChain()
optimizer2 = optimizers.SGD()
optimizer2.setup(model2)
losses=[]
verts = [ ]
batchsize=20
for i in range(1000):
x,y = get_batch(batchsize)
x_ = Variable(x.astype(np.float32).reshape(batchsize,1))
t_ = Variable(y.astype(np.float32).reshape(batchsize,1))
#Enregistrer la progression une fois toutes les 10 fois
if i%10==0:
w= model2.l1.W.data[0][0]
b = model2.l1.b.data[0]
verts.append((w,b))
model2.zerograds()
loss=model2(x_,t_)
loss.backward()
optimizer2.update(retain_grad=True)
#Tracez la progression
xs, ys = zip(*verts)
_=plt.plot(xs, ys, 'o', lw=1, color='white') #, ms=10)

L'axe horizontal est $ W $ et l'axe vertical est $ b $. Les courbes de niveau montrent la perte. Vous pouvez voir qu'il se dirige vers le bas.
Bien entendu, en raison de la simplification, le résultat de l'ajustement est droit même au point optimal. C'est la ligne droite la moins au carré. Il est montré ci-dessous.
x=np.linspace(0,1,100)
plt.plot(x,np.exp(x))
plt.hold(True)
p=model2.predict(Variable(x.astype(np.float32).reshape(100,1))).data
_=plt.plot(x, p,"r")

Avec ce qui précède, nous avons appris à utiliser le chainer en optimisant le réseau neuronal qui se rapproche de la fonction $ y = e ^ x $. C'est juste une touche, mais j'ai abordé le principe de l'optimisation et comment cela se déroule.
Recommended Posts