[PYTHON] [Computer Vision] Géométrie épipolaire apprise avec des chats

introduction

Le chat est mignon ~

Dans cet article, nous allons apprendre avec les chats ** la technologie pour restaurer le monde 3D à partir d'images multi-vues, qui est traitée dans le domaine de la vision par ordinateur **.

Ce domaine est encore à l'étude, et des formules parfois difficiles sortent, mais j'espère que la douleur sera neutralisée en apprenant avec les chats.

Cet article correspond au chapitre 5, "5.1 Géométrie épipolaire, 5.2 Calculs à l'aide de caméras et de structures 3D" dans "Practical Computer Vision" Faire.

Je souhaite restaurer le monde 3D à partir d'une image à vues multiples

L'image du chat au début était une image en deux dimensions. Alors, comment restaurer la forme tridimensionnelle de ce chat?

La bonne réponse est ** de photographier à partir de plusieurs perspectives tout en déplaçant la caméra vers le chat **.

En fonction de l'apparence du chat de chaque point de vue, le changement de posture de la caméra et la structure géométrique du chat que la caméra prend en photo sont calculés à nouveau.

Cela s'appelle Structure from Motion (SfM).

La procédure est la suivante.

• ** 1. Trouvez un point correspondant ** Les points correspondants sont, par exemple, une paire de points qui apparaissent dans chaque image lorsque la main du chat est vue sous différentes perspectives. La recherche des points correspondants dans l'image avant et après le déplacement du point de vue vous donne un indice sur la façon dont vous vous êtes déplacé.

• ** 2. Estimation du mouvement de la caméra ** Estimez comment le point de vue s'est déplacé, en utilisant les points correspondants comme indices.

• ** 3. Reconstruisez la scène 3D ** La forme tridimensionnelle est restaurée sur la base des points correspondants et du résultat de l'estimation du mouvement de la caméra.

• ** 4. Optimisation globale ** En répétant les étapes 2 et 3 à chaque fois que la caméra est déplacée, les erreurs de mouvement de caméra / de restauration de scène 3D s'accumulent. Pour résoudre ce problème, la précision globale est améliorée en trouvant la solution optimale qui minimise l'erreur entre la valeur mesurée et la valeur estimée en utilisant tous les points correspondants et les résultats d'estimation du mouvement du point de vue.

Pour simplifier le problème, considérez ici les paires d'images. En d'autres termes, considérez seulement deux points de vue.

Tout d'abord, je vais expliquer la théorie de base qui se produit entre ces images. Après cela, nous évaluerons le mouvement de la caméra et reconstruirons la scène 3D. L'optimisation globale de 4. est un processus qui n'est nécessaire que lorsqu'il y a beaucoup de points de vue, nous ne l'envisagerons donc pas ici.

La géométrie épipolaire est quoi?

Avant de déplacer la caméra ou de restaurer une scène 3D à partir d'une image à deux vues, il est nécessaire de comprendre la théorie de base de la géométrie épipolaire. La géométrie épipolaire est la géométrie qui se produit lorsque deux caméras capturent le même objet tridimensionnel à partir de perspectives différentes.

Les éléments qui systématisent la géométrie épipolaire sont le plan épipolaire, les lignes épipolaires, les épipoles, la matrice de base et la matrice de base, que nous présenterons ensuite.

Cinq mots super importants qui apparaissent dans la géométrie épipolaire

• ** Plan épipolaire ** (plan bleu sur la figure) En supposant que les centres optiques des deux caméras sont $ O_ {1} $ et $ O_ {2} $, les points tridimensionnels $ X $, $ O_ {1} $, $ O_ {2} $, soit un total de trois points Le plan par lequel il passe s'appelle le plan épipolaire. Le plan bleu sur la figure.

• ** Ligne épipolaire ** (ligne jaune sur la figure) Une ligne épipolaire est une ligne où le plan épipolaire et chaque plan image se croisent. Par exemple, lorsqu'un point tridimensionnel X apparaît comme un point x1 sur l'image 1, le même point X apparaît quelque part sur la ligne épipolaire sur l'image 2.

• ** Epipole ** (point rouge sur la figure) Les lignes épipolaires de toutes les images se croisent toujours en un point. C'est Epipole. Par conséquent, toutes les lignes épipolaires traversent des épipoles. Ce point est le point où le centre de la caméra de l'autre image est projeté sur votre image.

Points correspondants et lignes épipolaires dessinés sur l'image réelle:

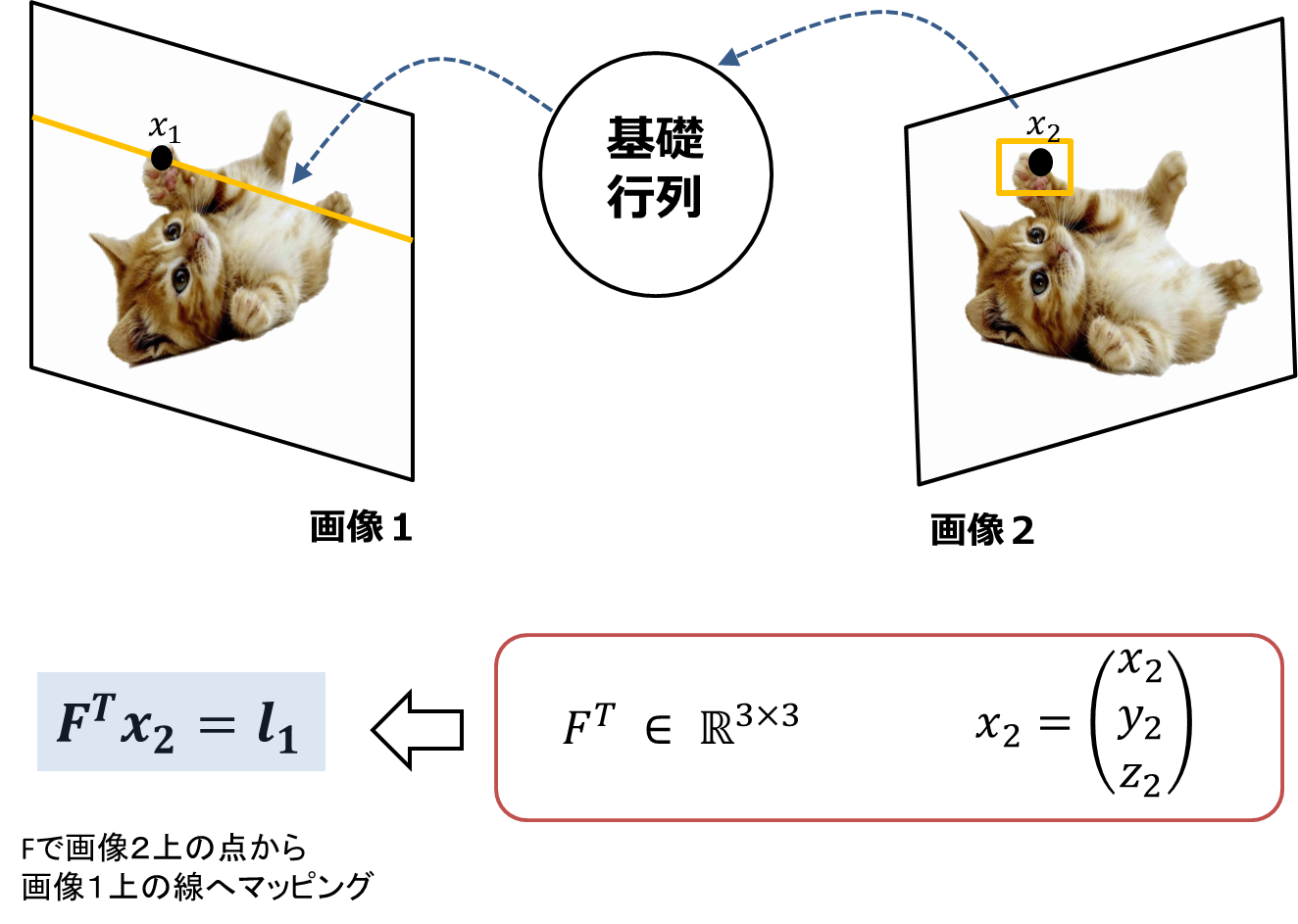
• ** Matrice fondamentale ** Il s'agit d'une matrice 3x3 et contient ** des informations de matrice interne / externe de la caméra. ** Il a également le rôle de ** mapper un point (dimension 0) sur une image à une ligne épipolaire (1 dimension) sur une autre image. Si cette matrice peut être estimée, elle peut être utilisée plus tard lors de l'estimation du mouvement de la caméra, etc., il est donc très important de trouver cette matrice correctement. Regardons de plus près ensuite.

• ** Matrice essentielle ** Semblable en nom à la matrice de base, mais un parent de la matrice de base. Il s'agit d'une matrice 3x3 et contient ** des informations sur la matrice externe de la caméra. ** Vous pouvez convertir $ F $ en $ E = K_ {2} FK_ {1} $ en utilisant la matrice interne de la caméra $ K $.

Matrice de base F

Apparition de la cérémonie de contention épipolaire

Si $ x_ {1} $ et $ x_ {2} $ sont des points de correspondance, la relation suivante est valable pour tous les points de correspondance $ x_ {1} $, $ x_ {2} $.

\boldsymbol{x_{2}^{T}}F\boldsymbol{x_{1}} = 0

$ F $ s'appelle la matrice de base et est une matrice 3x3. $ x_ {1} $, $ x_ {2} $ sont des vecteurs tridimensionnels qui représentent les coordonnées des points correspondants dans le ** système de coordonnées d'image dans le système de coordonnées simultanées.

Cette formule montre qu'il existe une relation de contrainte entre les points correspondants des deux images. ** Cette formule est appelée formule de contention épipolaire. ** Une fois le point de vue décidé, il sera décidé (= contrainte) de quel côté dans l'image 2 se trouve le point correspondant trouvé dans l'image 1. Et cette formule de contrainte ne dépend que de ** 2 points de vue et pas du tout de la scène 3D. ** **

Maintenant, vérifions si $ \ boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}} = 0 $ tient.

Puisque $ x_ {1} $ est un point sur l'image 1, il est exprimé comme $ x_ {1} = (x_ {1}, y_ {1}, z_ {1}) ^ {T} $ ($ z_ {1) } $ Est 1).

D'autre part, puisque F est une matrice 3x3, $ Fx_ {1} $, qui est le produit de $ x_ {1} $, est un vecteur tridimensionnel. Soit ce vecteur $ Fx_ {1} = (a, b, c) ^ T $.

Ce $ Fx_ {1} = (a, b, c) ^ T $ est le coefficient de la ligne épipolaire sur l'image 2. Ensuite, multiplier ce coefficient par x2 sur la ligne épipolaire montre que l'équation linéaire $ ax + par + c = 0 $ est satisfaite. En d'autres termes, $ \ boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}} = 0 $ tient!

Inversement, si le résultat de la substitution de $ x_ {2} $ n'est pas 0, alors on peut dire que ce point $ x_ {2} $ ne correspond pas à x1 (voir la figure ci-dessous).

Lors de la recherche du point correspondant $ x_ {2} $ dans l'image 2 du point $ x_ {1} $ dans l'image 1, au lieu de rechercher l'image entière dans ** image 2, $ x_ {1} $ Seule la ligne épipolaire $ l_ {2} $ projetée sur l'image 2 doit être recherchée **, de sorte que le coût du calcul et le taux de réponse aux erreurs diminuent.

À propos, l'équation ci-dessus $ \ boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}} = 0 $ mappe le point $ x_ {1} $ de l'image 1 sur l'image 2 sous forme de ligne droite. Cela représente le cas. Au contraire, lorsque le point $ x_ {2} $ sur l'image 2 est mappé sur l'image 1 sous forme de ligne droite, l'équation suivante est obtenue et les deux côtés sont transposés, donc c'est mathématiquement le même. ($ (\ Boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}}) ^ {T} = $ La formule suivante)

\boldsymbol{x_{1}^{T}}F^{T}\boldsymbol{x_{2}} = 0

Le fait est que les positions de $ x_ {1} $ et $ x_ {2} $ sont permutées et F est transposée.

1. Trouvez F

Alors, comment trouvez-vous F? Il existe plusieurs méthodes typiques pour cela.

• ** Algorithme en 8 points ** Estimer F en utilisant 8 points correspondants ou plus. Résolvez avec la méthode des moindres carrés en utilisant SVD. Pour une utilisation pratique, utilisez l'algorithme normalisé à 8 points.

• ** Algorithme normalisé à 8 points ** Une version améliorée de l'algorithme en 8 points. En tant que processus de normalisation, l'origine est amenée au centre de gravité du groupe de points des points correspondants et la distance moyenne du centre de gravité à chaque point correspondant est fixée à $ \ sqrt2 $, de sorte que la précision est considérablement améliorée. [Implémentation d'algorithme normalisé en 8 points] (http://www.peterkovesi.com/matlabfns/Projective/fundmatrix.m) Mise en œuvre de la normalisation

• ** Minimisation des coûts algématiques (répétition) ** Plus précis que l'algorithme normalisé à 8 points.

• ** Minimisez l'erreur de distance entre le point d'observation et le point d'estimation ** Après avoir donné F comme valeur initiale par la méthode ci-dessus, calculez une fois la position de X et projetez-la sur l'image. Minimisez la distance (erreur) entre le point d'observation et le point d'estimation en tant que fonction de coût. On dit qu'il s'agit de l'algorithme Gold Standard et qu'il a la plus grande précision.

De plus, si les deux matrices de caméras sont connues, vous pouvez également les trouver Implémentation

Algorithme en 8 points

Voici un aperçu de l'algorithme en 8 points le plus basique (voir le lien ci-dessus pour une implémentation détaillée).

L'expression de contrainte épipolaire $ \ boldsymbol {x_ {2} ^ {T}} F \ boldsymbol {x_ {1}} = 0 $ donne une équation pour chaque point de correspondance i:

Puisque la variable inconnue est ici une matrice F, nous résumerons F et résoudrons pour f sous la forme de l'équation Af = 0. Ici, F est une matrice 3x3, mais comme l'échelle est indéfinie, elle peut être résolue s'il y a pratiquement 8 points correspondants. Le nom de "l'algorithme en 8 points" vient d'ici.

Après le démontage avec SVD, utilisez que F est le rang 2. Si la singularité minimale de la composante diagonale de Σ est fixée à 0 et résolue, la précision de F augmentera. Le côté gauche de la figure ci-dessous est le cas où la contrainte de rang 2 n'est pas appliquée, et le côté droit est le cas où la contrainte de rang 2 est appliquée.

Cité de la référence [1].

2. Trouvez la matrice de caméra à partir de F

Alors pourquoi avons-nous trouvé F? Parce que nous pouvons trouver la matrice de caméra P à partir de ** F **.

Comme mentionné précédemment, F contient une matrice de caméra interne et une matrice de caméra externe. Par conséquent, si F est décomposé en matrices de caméra interne et externe, la matrice de caméra peut être estimée à partir de F.

Cependant, la précision de l'estimation dépend du fait que la caméra a été calibrée à l'avance ou non. Si les paramètres internes de la caméra sont inconnus, seule la transformation de projection peut être estimée à partir de F.

Le déroulement du processus de F à l'estimation de la matrice de la caméra est illustré dans la figure ci-dessous.

Si la caméra n'est pas calibrée

Si la caméra n'est pas étalonnée, c'est-à-dire si les paramètres internes de la caméra sont inconnus, les paramètres internes et externes de la caméra doivent être estimés. Dans ce cas, ** la matrice de la caméra ne peut être estimée que jusqu'à la transformation de projection. ** **

Normalement, vous pouvez trouver P de F dans un, mais ** au contraire, vous ne pouvez pas trouver P de F dans un **. En effet, les matrices de base des deux ensembles d'images projetées sont les mêmes.

Par exemple, F dans la matrice de caméra (P, P'H) et F dans la matrice de caméra (PH, P'H) sont identiques.

La matrice de caméra $ P_ {1} $, $ P_ {2} $ est la suivante. × est le produit extérieur.

P_{1}=[I|0]Et P_{2} =[[e_{2}]×F|e_{2}]

Si la caméra a été calibrée

Si la caméra a été calibrée, il vous suffit d'estimer les paramètres externes de la caméra. Tous les paramètres peuvent être estimés à l'exception de l'échelle de translation. F a l'ambiguïté de la transformation de projection, tandis que E a l'ambiguïté d'avoir quatre solutions.

Tout d'abord, trouvez la matrice de base E à partir de F en utilisant $ E = K_ {2} FK_ {1} $. Ensuite, décomposez E avec SVD. Puisque E a det (E) = 0 et que les valeurs singulières autres que 0 sont égales et que leurs grandeurs sont indéfinies, la composante diagonale de Σ peut s'écrire (1,1,0). En d'autres termes, il peut être décomposé par SVD comme suit.

E=Udiag(1,1,0)V^{T}

$ u_ {3} $ est le vecteur de la troisième colonne de $ U $

W = \begin{pmatrix}
0 & -1 & 0 \\
1 & 0 & 0 \\
0 & 0 & 1 
\end{pmatrix}

Puis, à la fin, les quatre solutions suivantes apparaîtront dans la matrice de la caméra.

Parmi ceux-ci, un seul a la scène devant la caméra, donc (a) est la bonne solution. (Figure ci-dessous)

Cité de la référence [1].

3. Reconstruisez le monde 3D

La matrice de caméra P a été obtenue. Reconstruisons enfin le monde tridimensionnel.

Levé triangulaire

L'enquête triangulaire estime X qui satisfait simultanément les formules de conversion de caméra suivantes obtenues à partir de deux points de vue.

Cité de la référence [1].

À partir de la formule de conversion de la caméra où la matrice de la caméra est $ P_ {1} $, $ P_ {2} $

\lambda_{1}x_{1} = P_{1}X

\lambda_{2}x_{2} = P_{2}X

Donc, si vous l'exprimez dans une matrice,

\begin{bmatrix}
P_{1} & -x_{1} & 0 \\
P_{2} & 0 & -x_{2} 
\end{bmatrix}
\begin{bmatrix}
X \\
\lambda_{1}\\
\lambda_{2} 
\end{bmatrix}
=0

Ce sera.

Comme il est également sous la forme Ax = 0, 3D X peut être restauré en résolvant x avec SVD.

la mise en oeuvre

• ykoga/cv_tutorial_epipolar (OpenCV)
• À partir d'OpenCV3.1 (publié le 12/12/2015), le module sfm avec la fonction Structure From Motion a été ajouté.

Matériel de référence

• Livres [1] Multiple View Geometry in Computer Vision
  [2] Vision par ordinateur pratique
• La mise en oeuvre MATLAB and Octave Functions for Computer Vision and Image Processing
• Image Pakutaso GATAG ｜ Free Image / Photo Material Collection 3.0
• Autre Chanson de la matrice fondamentale