[PYTHON] We will implement the optimization algorithm (Kujira-san algorithm)
Introduction
A series of optimization algorithm implementations. First, look at Overview.
The code can be found on github.
Kujira's algorithm
Overview
The Whale Optimization Algorithm (WOA) is an algorithm created by focusing on the predatory behavior of whales. Whales prey on prey by swarm behavior called bubble nets. The bubble net seems to be an action of hunting down and preying on prey while drawing a circle as shown in the figure.

reference ・ Kujira-san algorithm ・ Whale Optimization Algorithm
algorithm
Find the prey by choosing one of the three actions of approaching the prey, searching for the prey, and drawing a circle.
- Algorithm flow

- Term correspondence
| problem | Kujira's algorithm |
|---|---|
| Input to the problem | Whale position ≒ prey position |
| Evaluation value | クジラの位置におけるEvaluation value |
- Regarding hyperparameters
| Variable name | meaning | Remarks |
|---|---|---|
| a_decrease | Decrease value of a | It moves randomly at first and approaches its prey in the second half. a is the transition speed |
| logarithmic_spiral | Logarithmic spiral coefficient | The bigger it is, the bigger it moves when it turns |
Approaching prey
I wrote that it is approaching the prey, but I do not know where the prey is actually, so I treat the whale with the highest evaluation at present as a prey and approach it.
First, issue $ \ vec {A} $ and $ \ vec {C} $.
$ \ vec {r_1} $ and $ \ vec {r_2} $ are random numbers from 0 to 1 in the same dimension as the coordinates. $ a $ is a variable that decreases step by step from the initial value 2. ($ 2 \ geqq a \ geqq 0 $)
here
The formula for approaching prey is as follows.
$ \ Vec {X} $ represents your coordinates and $ \ vec {X_ {best}} $ is the most highly rated whale. The code is as follows.
import numpy as np
a = 2 #Decrease every step
r1 = np.random.rand(problem.size) # 0-Generate a random number of 1
r2 = np.random.rand(problem.size) # 0-Generate a random number of 1
A = (2.0 * np.multiply(a, r1)) - a
C = 2.0 * r2
i =Index of target whale
if np.linalg.norm(A) < 1:
pos = np.asarray(whales[i].getArray()) #Coordinates of the target whale
best_pos = np.asarray(best_whale.getArray()) #Best whale coordinates
D = np.linalg.norm(np.multiply(C, best_pos) - pos)
pos = best_pos - np.multiply(A, D)
Search for prey
Explained in approaching prey
$ \ vec {X_p} $ is the coordinates of a random whale.
import numpy as np
i =Index of target whale
if np.linalg.norm(A) >= 1:
pos = np.asarray(whales[i].getArray()) #Coordinates of the target whale
p_pos = np.asarray(whales[random.randint(0, len(whales)-1)].getArray()) #Random whale coordinates
D = np.linalg.norm(np.multiply(C, p_pos) - pos)
pos = p_pos - np.multiply(A, D)
Draw a circle
The circle is drawn by the following formula based on the prey (the whale with the maximum evaluation value).
$ b $ is the coefficient of the logarithmic spiral (is logarithmic_spiral) and $ L $ is a random value of [-1, 1].
import numpy as np
i =Index of target whale
pos = np.asarray(whales[i].getArray()) #Coordinates of the target whale
best_pos = np.asarray(best_whale.getArray()) #Best whale coordinates
#spin
D = np.linalg.norm(best_pos - pos)
L = np.random.uniform(-1, 1, problem.size) # [-1,1]Random number
_b = logarithmic_spiral
pos = np.multiply(np.multiply(D, np.exp(_b*r)), np.cos(2.0*np.pi*r)) + best_pos
Spiral graph
I drew a circle, but I tried to see how it was moving.
The x-axis of the graph is a random number from -1 to 1 ($ L $), and the y-axis is the distance traveled. If it is a mathematical formula, only the following part is graphed.
- Changes due to Euclidean distance
It is a graph when $ b $ (logarithmic_spiral) is fixed to 1 and only $ \ vec {D'} $ is changed. Since $ \ vec {D'} $ represents the Euclidean distance between you and your prey (best whale), it can be said that it represents the change in movement depending on the distance to your prey.

You can see that the farther away you are, the more likely you are to move.
- Changes due to logarithmic spiral coefficient
This time it is the case of changing $ b $ (logarithmic_spiral). $ D'$ is fixed at 1.

As with $ D'$, the larger the $ b $, the greater the change.
Whole code
The whole code. When creating the code, I refer to Code here.
import math
import random
import numpy as np
class WOA():
def __init__(self,
whale_max, #Number of whales
a_decrease=0.001, #Decreased value of variable a
logarithmic_spiral=1, #Logarithmic spiral coefficient
):
self.whale_max = whale_max
self.a_decrease = a_decrease
self.logarithmic_spiral = logarithmic_spiral
def init(self, problem):
self.problem = problem
self.best_whale = None
self.whales = []
for _ in range(self.whale_max):
o = problem.create()
self.whales.append(o)
if self.best_whale is None or self.best_whale.getScore() < o.getScore():
self.best_whale = o.copy()
self._a = 2
def step(self):
for whale in self.whales:
pos = np.asarray(whale.getArray())
if random.random() < 0.5:
r1 = np.random.rand(self.problem.size) # 0-Random number of 1
r2 = np.random.rand(self.problem.size) # 0-Random number of 1
A = (2.0 * np.multiply(self._a, r1)) - self._a
C = 2.0 * r2
if np.linalg.norm(A) < 1:
#Approaching prey
new_pos = self.best_whale.getArray()
else:
#Search for prey
new_pos = self.whales[random.randint(0, len(self.whales)-1)].getArray()
new_pos = np.asarray(new_pos)
D = np.linalg.norm(np.multiply(C, new_pos) - pos)
pos = new_pos - np.multiply(A, D)
else:
#spin
best_pos = np.asarray(self.best_whale.getArray())
D = np.linalg.norm(best_pos - pos)
L = np.random.uniform(-1, 1, self.problem.size) # [-1,1]Random number
_b = self.logarithmic_spiral
pos = np.multiply(np.multiply(D, np.exp(_b*L)), np.cos(2.0*np.pi*L)) + best_pos
whale.setArray(pos)
if self.best_whale.getScore() < whale.getScore():
self.best_whale = whale.copy()
self._a -= self.a_decrease
if self._a < 0:
self._a = 0
Hyperparameter example
It is the result of optimizing hyperparameters with optuna for each problem. One optimization trial yields results with a search time of 5 seconds. I did this 100 times and asked optuna to find the best hyperparameters.
| problem | a_decrease | logarithmic_spiral | whale_max |
|---|---|---|---|
| EightQueen | 0.020366541568838378 | 1.5723091675627572 | 45 |
| function_Ackley | 0.012846425355295324 | 1.817054209171554 | 49 |
| function_Griewank | 0.014055305155620233 | 1.5507180701447845 | 48 |
| function_Michalewicz | 0.019651164901908023 | 1.7671279692872293 | 46 |
| function_Rastrigin | 0.0173318428180831 | 0.7578390758302801 | 46 |
| function_Schwefel | 0.007491644624065206 | 1.6917050129680944 | 9 |
| function_StyblinskiTang | 0.024426401837372255 | 1.9474471085818506 | 50 |
| function_XinSheYang | 0.005722874915111857 | 0.4779624408790928 | 24 |
| g2048 | 0.043666294831303784 | 1.09050483219953 | 37 |
| LifeGame | 0.0054058667884643585 | 0.06834119701477159 | 50 |
| OneMax | 0.014922301994610046 | 0.8650190784964947 | 27 |
| TSP | 0.0287871077043457 | 1.3855183848189636 | 45 |
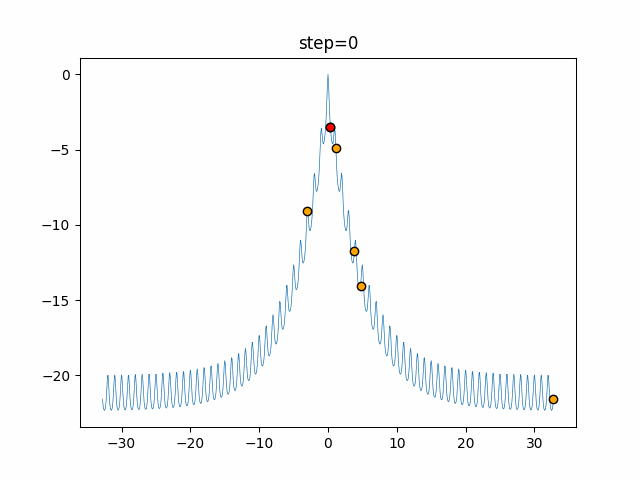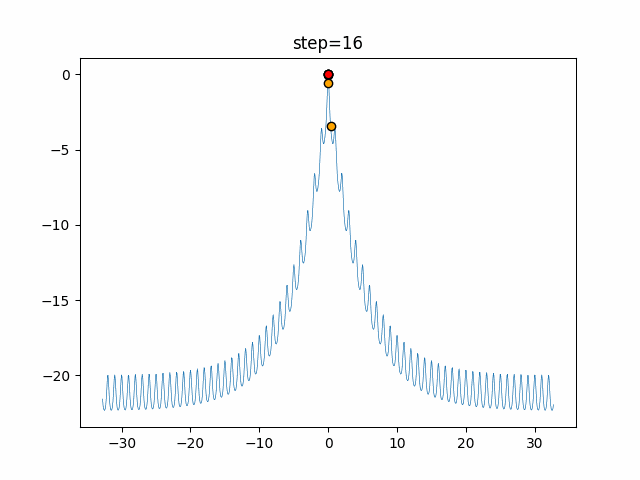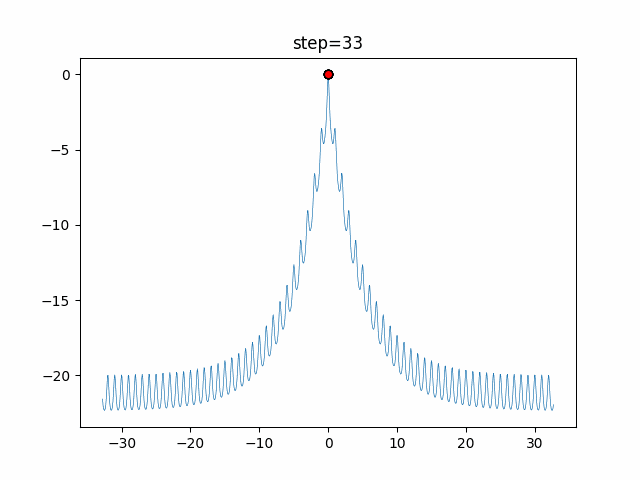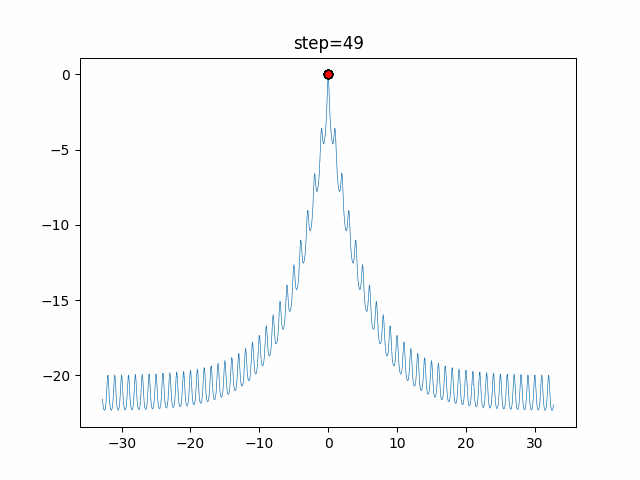
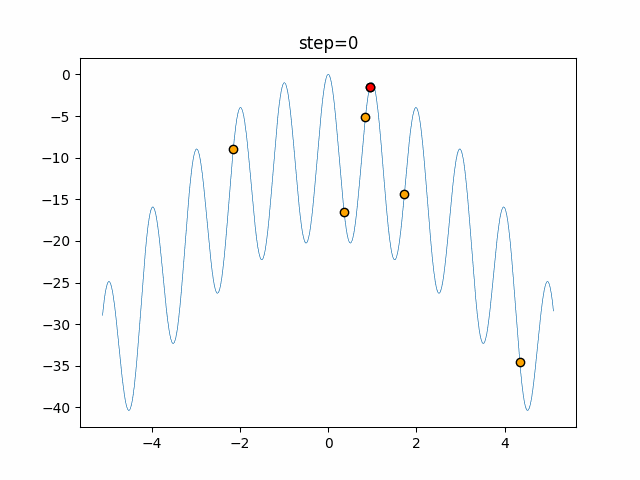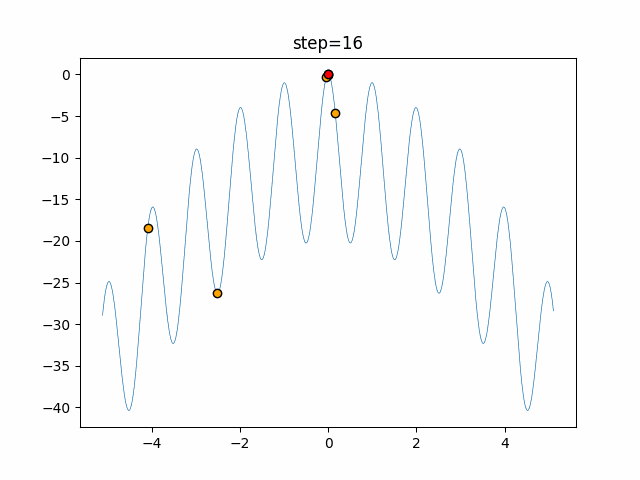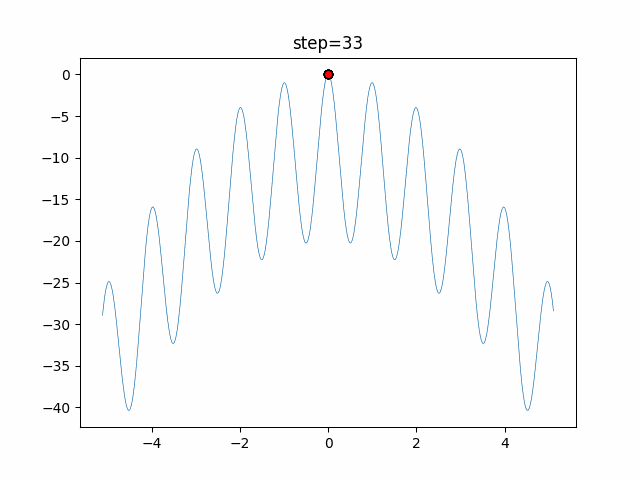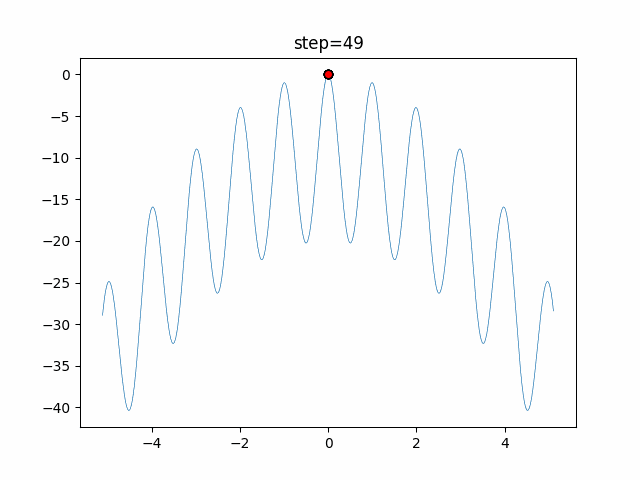
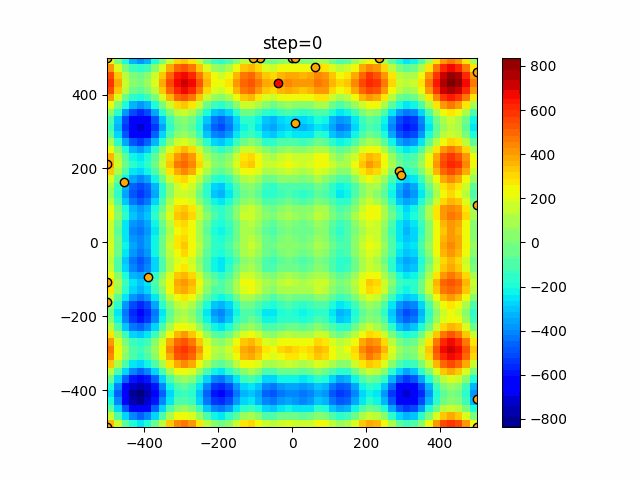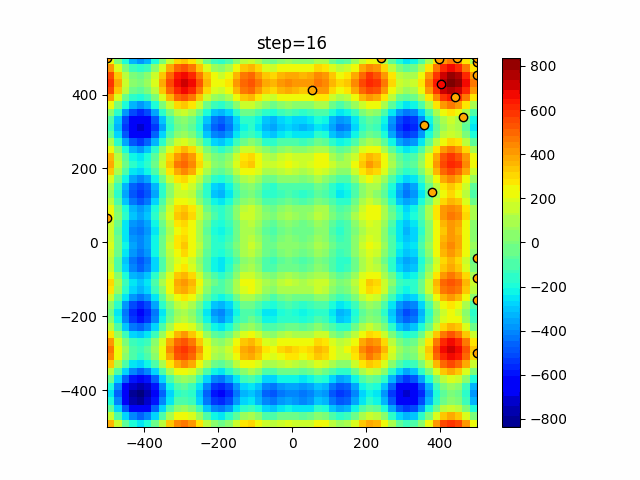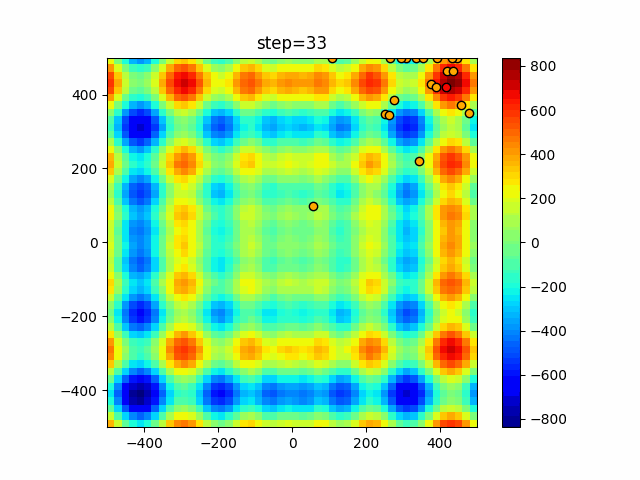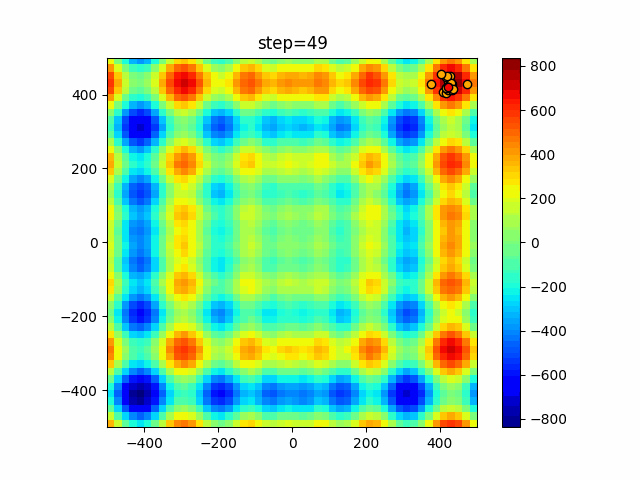
Visualization of actual movement
The 1st dimension is 6 individuals, and the 2nd dimension is 20 individuals, which is the result of 50 steps. The red circle is the individual with the highest score in that step.
The parameters were executed below.
WOA(N, a_decrease=2/50, logarithmic_spiral=1)
function_Ackley
- 1D
- 2D
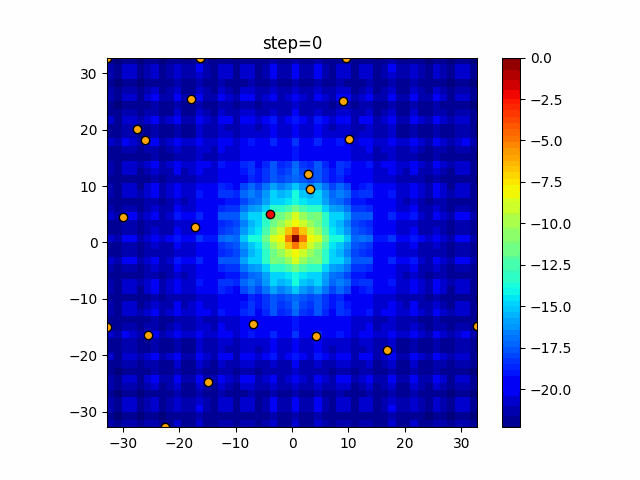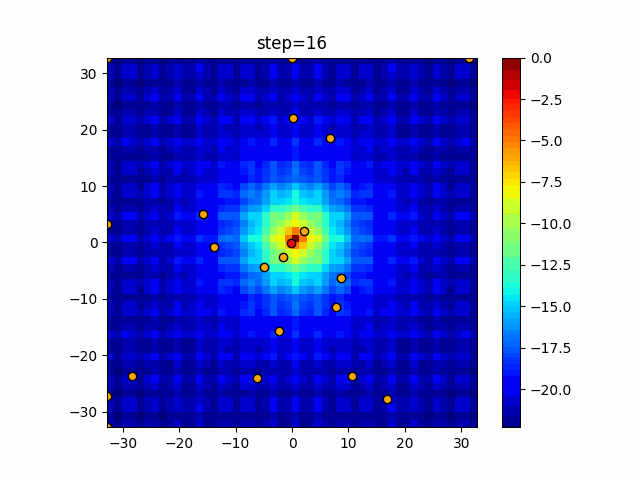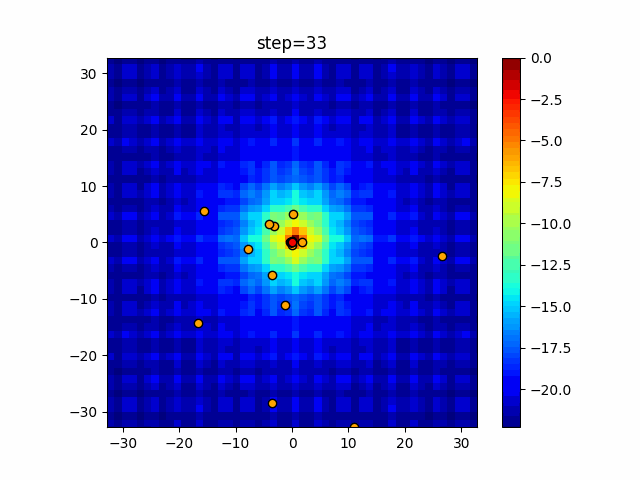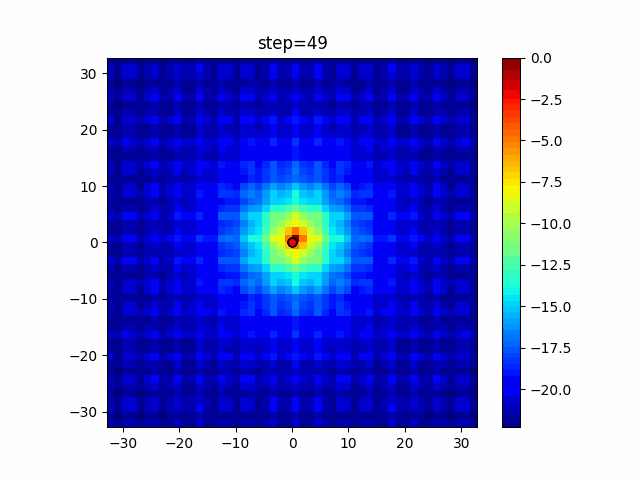
function_Rastrigin
- 1D
- 2D
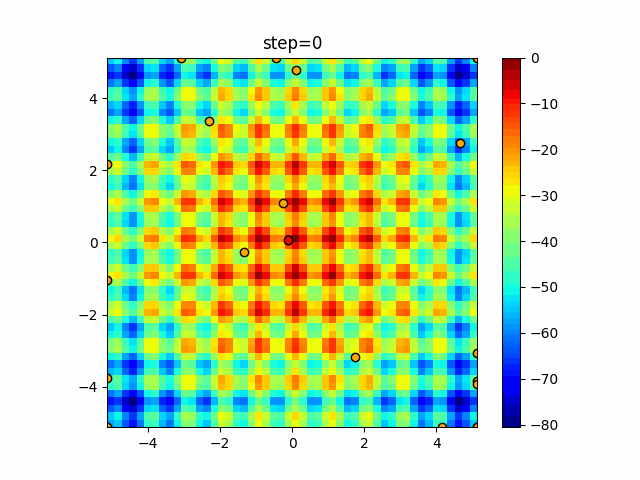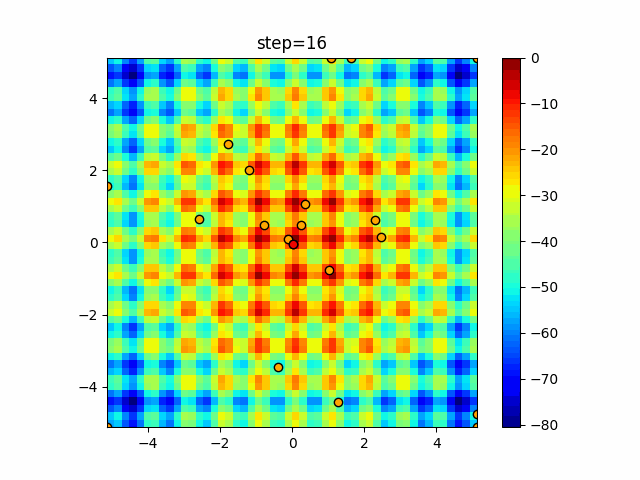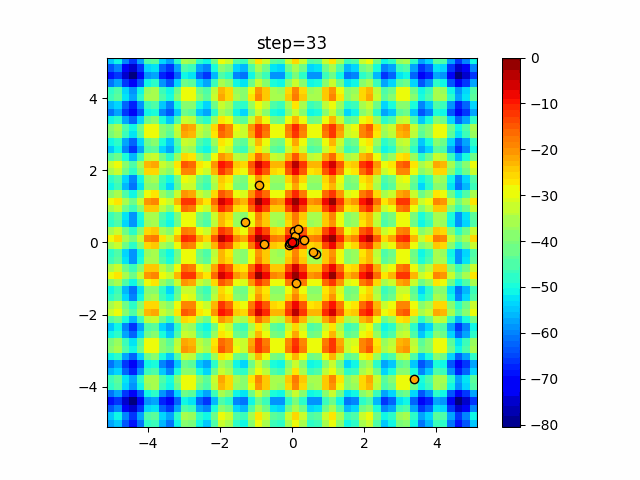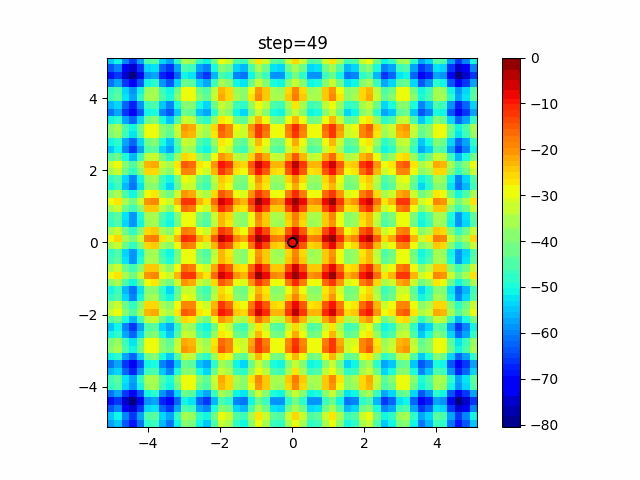
function_Schwefel
- 1D
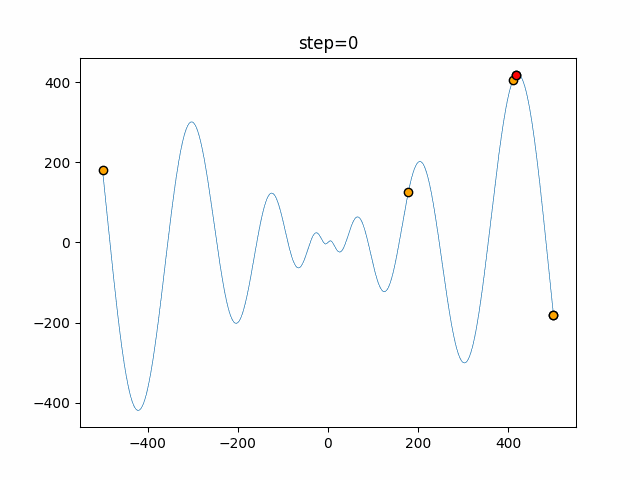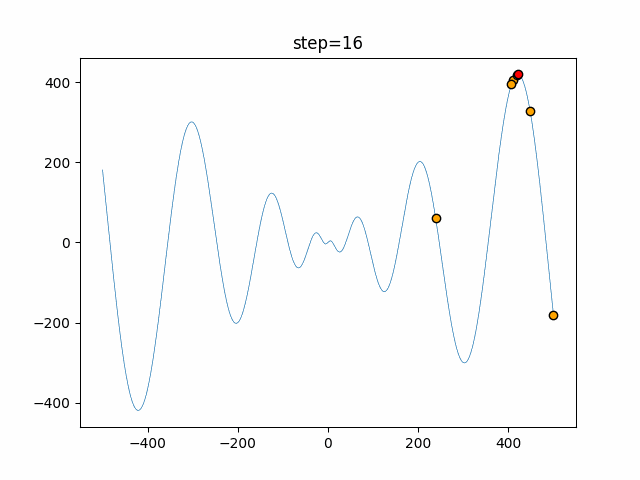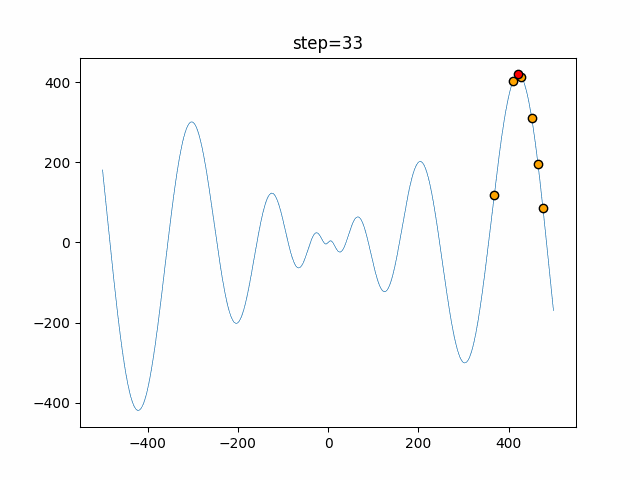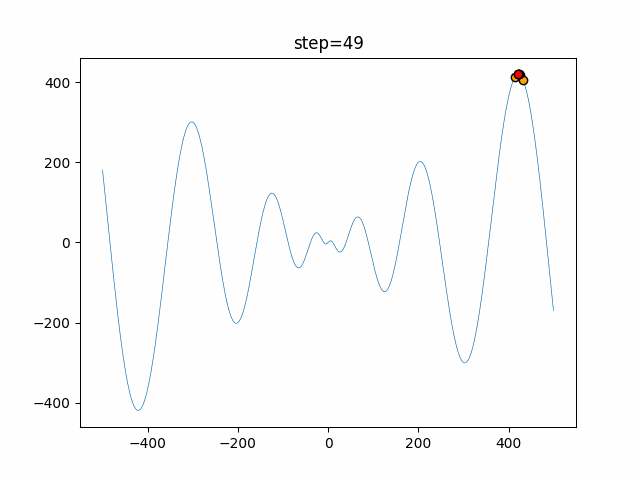
- 2D
function_StyblinskiTang
- 1D
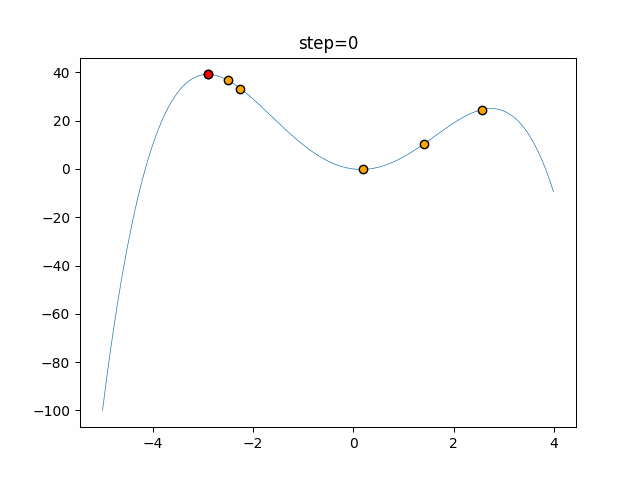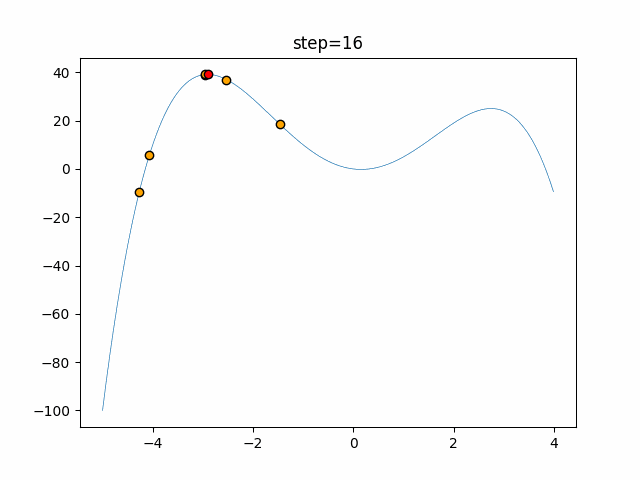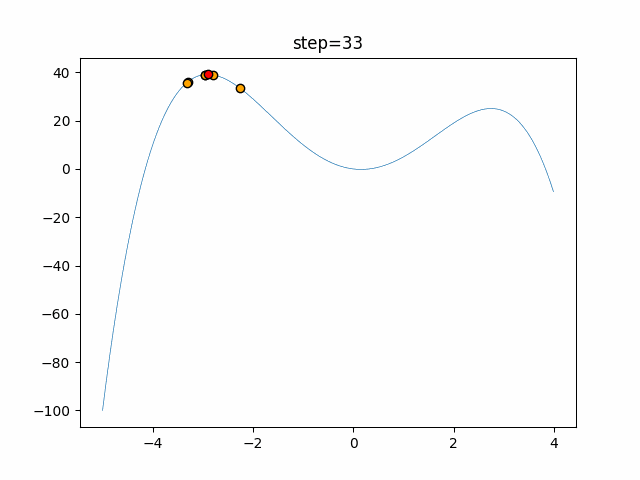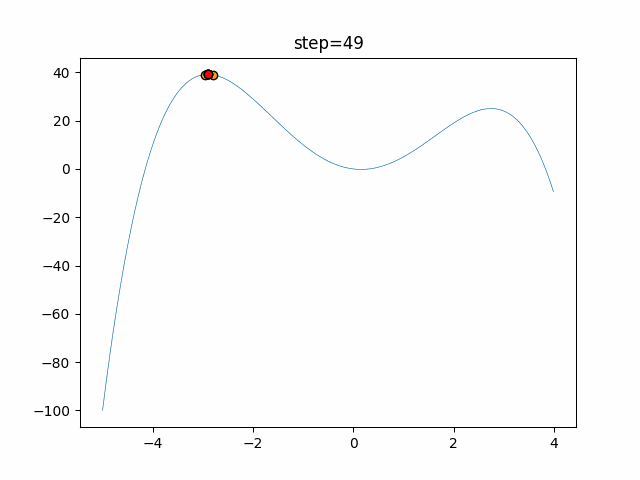
- 2D
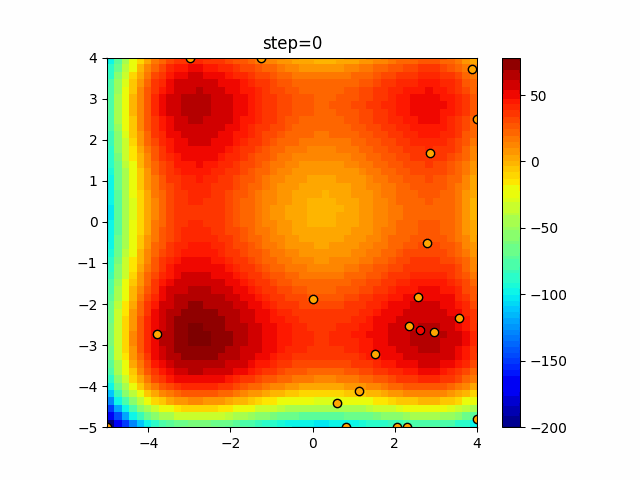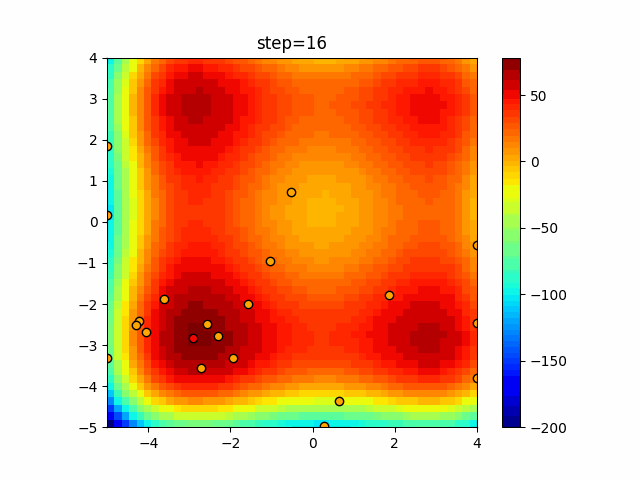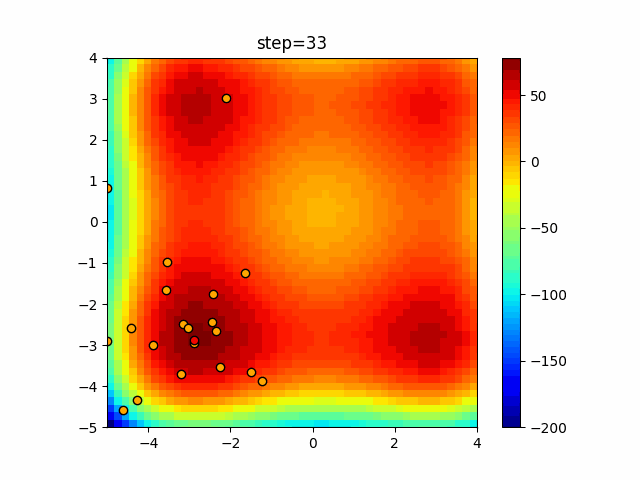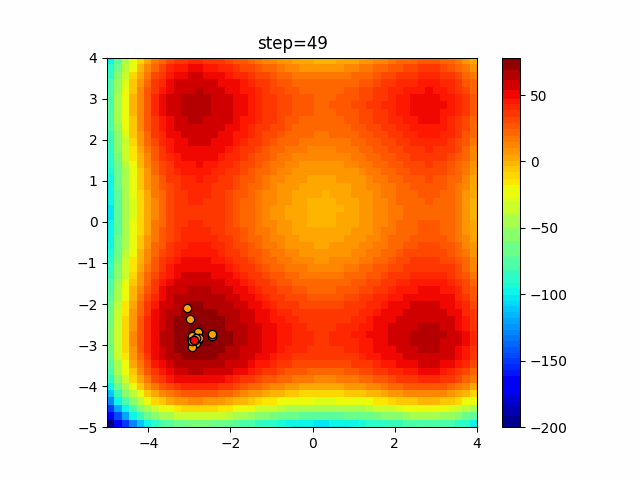
function_XinSheYang
- 1D
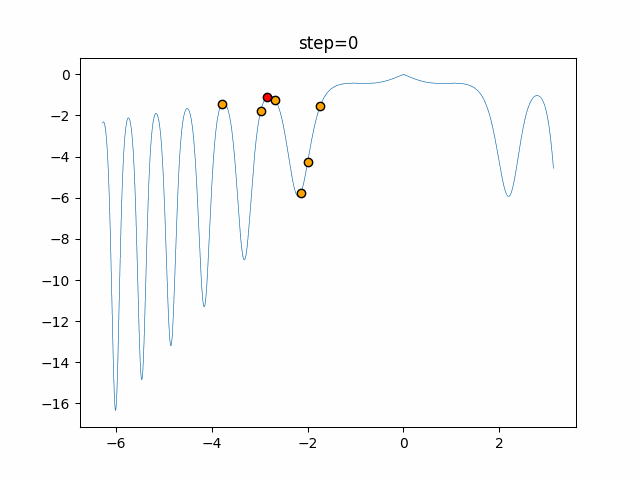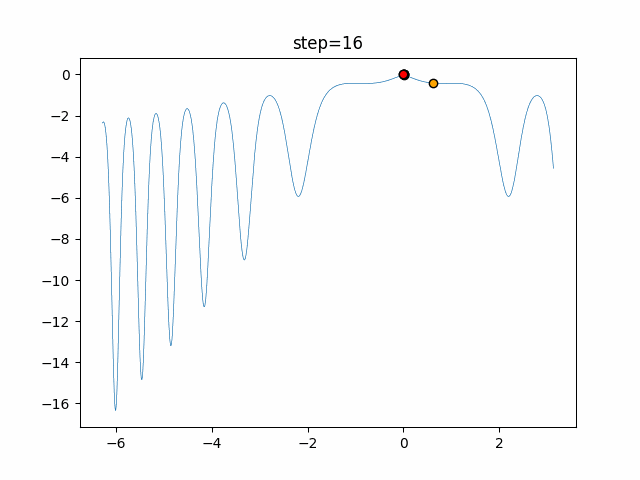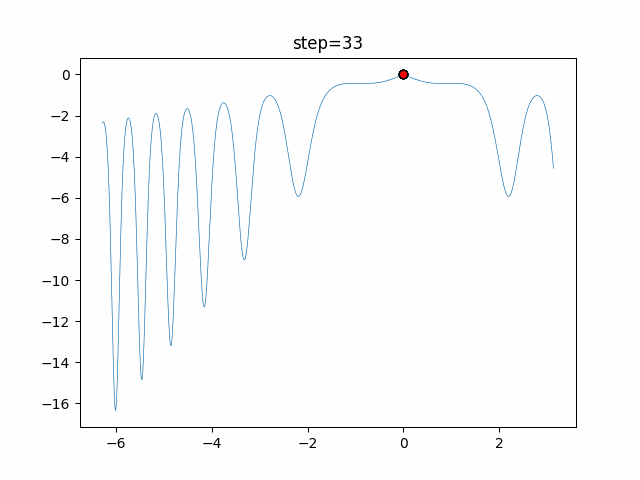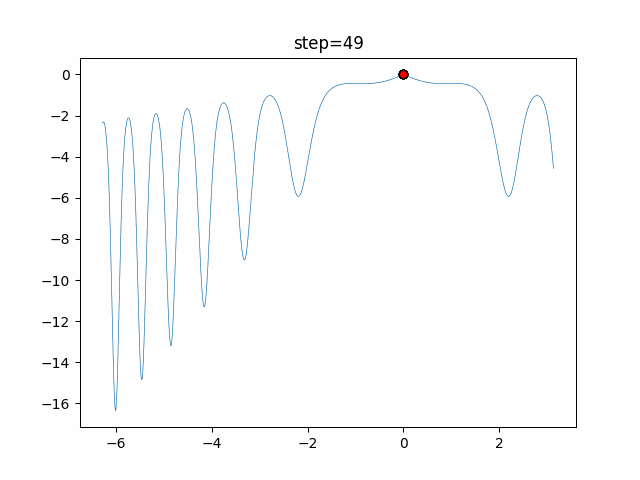
- 2D

Afterword
It gathers in a nice way while swirling around. However, once it converges, it will not escape from it, so it seems important how to control the value of a.
Recommended Posts