 | Introduction to Computational Physics
(2000 / 12)
Harvey Gold, Jant Bochinik, etc.
View product details
Is referred to.
Many things that grow by randomly adding basic units to the natural world, such as the formation of lightning-shaped cracks in snowflakes and geological faults, and the growth of bacterial colonies, can be seen. One of the well-known models is Diffusion-Limited Aggregation (DLA). This model is an example of how random movements produce beautiful self-similar clusters.
The steps of cluster growth are
- One kind of particle occupies one lattice point
- Emit a single particle from around the seed-centered circle
- Randomly walk the particles
- When you reach a point around one, it adheres to it → Go to 2
Repeat this process until a large cluster is formed (typically thousands to millions of times). Also, in order to reduce the amount of calculation, we will remove the particles that have gone too far from the cluster in step 3 and start over from step 2.
In order to actually realize this operation, we can see that it is only necessary to have a matrix representing the grid and an array that records the points around the occupied grid points. The random walk part is used many times, but it generates a uniform random number and determines the direction of up, down, left, and right based on the size of the value. Also, when actually simulating, the random walk at a position far from the cluster consumes most of the CPU time and becomes inefficient, so try increasing the stride length of the random walk at a position far from the cluster. It was. We captured the actual simulation (cluster was generated for N = 200, 500, 1000), so you can check it below.
http://youtu.be/qLii4DlBnv0
I haven't edited anything, so it's ugly, but w
a, b, c mean a, b, c of the textbook problem, and a creates a cluster with the number of particles specified in the entry box. b and c are for finding the adhesion probability by Monte Carlo simulation and for actually finding the fractal dimension. If you are interested, please refer to the source code.
The clusters obtained when N = 500 are as follows.
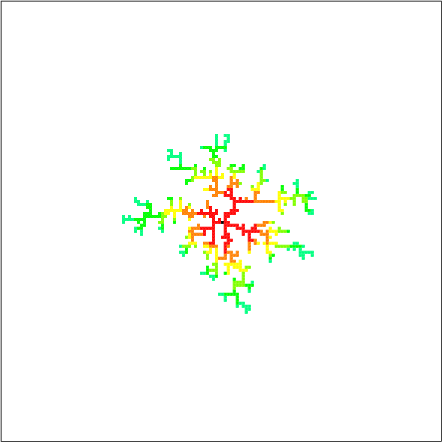
Link ( Easy Chemical Experiment-Making a Beautiful Silver Tree </ strong> Don't you think it looks a lot like the image of silver tree in a>)? In fact, since the random walk is equivalent to diffusion, it can be said that the simulation itself is based entirely on the generation of metal trees, and of course the shapes of the resulting figures are very similar.
The source code is all listed below.
The function pr for saving Canvas is likely to be used frequently in the future. SetParameter is also one of the classes I have been using for a long time. I'd like to summarize it a little more, but I'm not in trouble with this at the moment, so I think I'll continue to use it for a while.
DLA.py
#! /usr/bin/env python
# -*- coding:utf-8 -*-
#
# written by ssh0, August 2014.
from Tkinter import *
import numpy as np
import matplotlib.pyplot as plt
import random
import time
class DLA(object):
def __init__(self, N, view=True, color=True):
self.r = 3
self.N = N
self.view = view
self.color = color
self.L = int(self.N**(0.78))
if self.view:
self.default_size = 640 # default size of canvas
self.rsize = int(self.default_size/(2*self.L))
if self.rsize == 0:
self.rsize = 1
fig_size = 2*self.rsize*self.L
self.margin = 10
self.sub = Toplevel()
self.canvas = Canvas(self.sub, width=fig_size+2*self.margin,
height=fig_size+2*self.margin)
self.c = self.canvas.create_rectangle
self.update = self.canvas.update
self.sub.title('DLA cluster')
self.c(self.margin, self.margin,
fig_size+self.margin, fig_size+self.margin,
outline='black', fill='white')
self.canvas.pack()
self.start_time = time.time()
def grow_cluster(self):
lattice = np.zeros([self.L*2+1, self.L*2+1], dtype=int)
#Seed grid points
self.center = self.L
lattice[self.center, self.center] = 1
if self.view:
c = self.c
rect = c((2*self.center-self.L)*self.rsize+self.margin,
(2*self.center-self.L)*self.rsize+self.margin,
(2*(self.center+1)-self.L)*self.rsize+self.margin-1,
(2*(self.center+1)-self.L)*self.rsize+self.margin-1,
outline='black', fill='black')
rn = np.random.rand
def reset():
"""Selection of initial point"""
theta = 2*np.pi*rn()
x = int((self.r+2)*np.cos(theta))+self.center
y = int((self.r+2)*np.sin(theta))+self.center
return x, y
x, y = reset()
l = 1
n = 0
while n < self.N:
#Increase your stride far from the periphery of the cluster
r = np.sqrt((x-self.center)**2+(y-self.center)**2)
if r > self.r+2:
l = int(r-self.r-2)
if l == 0: l = 1
else:
l = 1
#Random walk
p = rn()*4
if p < 1:
x += l
elif p < 2:
x -= l
elif p < 3:
y += l
else:
y -= l
r = np.sqrt((x-self.center)**2+(y-self.center)**2)
#Redo the process at a point away from the center point
if r >= 2*self.r:
x, y = reset()
continue
judge = np.sum(lattice[x-1,y]+lattice[x+1,y]
+lattice[x,y-1]+lattice[x,y+1])
#Incorporate particles into a cluster
if judge > 0:
lattice[x, y] = 1
#drawing
if self.view:
if self.color:
colors = ['#ff0000', '#ff8000', '#ffff00', '#80ff00',
'#00ff00', '#00ff80', '#00ffff', '#0080ff',
'#0000ff', '#8000ff', '#ff00ff', '#ff0080']
color = colors[int(n/100)%len(colors)]
else:
color = "black"
rect = c((2*x-self.L)*self.rsize+self.margin,
(2*y-self.L)*self.rsize+self.margin,
(2*(x+1)-self.L)*self.rsize+self.margin-1,
(2*(y+1)-self.L)*self.rsize+self.margin-1,
outline=color, fill=color)
self.update()
#rmax update
if int(r)+1 > self.r:
self.r = int(r) + 1
x, y = reset()
n += 1
else:
if self.view:
self.end_time = time.time()
t = self.end_time-self.start_time
print "done; N = %d, time = " % self.N + str(t) + ' (s)'
return lattice
class SetParameter():
def show_setting_window(self, parameters, commands):
""" Show a parameter setting window.
parameters: A list of dictionaries {'parameter name': default_value}
commands: A list of dictionary {'name of button': command}
"""
self.root = Tk()
self.root.title('Parameter')
frame1 = Frame(self.root, padx=5, pady=5)
frame1.pack(side='top')
self.entry = []
for i, parameter in enumerate(parameters):
label = Label(frame1, text=parameter.items()[0][0] + ' = ')
label.grid(row=i, column=0, sticky=E)
self.entry.append(Entry(frame1, width=10))
self.entry[i].grid(row=i, column=1)
self.entry[i].delete(0, END)
self.entry[i].insert(0, parameter.items()[0][1])
self.entry[0].focus_set()
frame2 = Frame(self.root, padx=5, pady=5)
frame2.pack(side='bottom')
self.button = []
for i, command in enumerate(commands):
self.button.append(Button(frame2, text=command.items()[0][0],
command=command.items()[0][1]))
self.button[i].grid(row=0, column=i)
self.root.mainloop()
class Main(object):
def __init__(self):
import sys
self.sp = SetParameter()
self.dla = None
self.b = None
self.sp.show_setting_window([{'N': 200}],
[{'a': self.exp_a},
{'b': self.exp_b},
{'c': self.exp_c},
{'c:fit': self.fitting},
{'save': self.pr},
{'quit': sys.exit}])
def exp_a(self):
self.N = int(self.sp.entry[0].get())
self.dla = DLA(self.N)
lattice = self.dla.grow_cluster()
def exp_b(self):
trial = 3000
self.dla2 = DLA(2, view=False)
self.dla2.L = 6
distribution = {'p': 0, 'q': 0, 'r': 0, 's': 0}
#Classification
for i in range(trial):
lattice = self.dla2.grow_cluster()
l = lattice[self.dla2.L-1:self.dla2.L+2,
self.dla2.L-1:self.dla2.L+2]
if np.sum(l) == 2:
distribution['r'] += 1
elif np.sum(l[0,1]+l[1,0]+l[1,2]+l[2,1]) == 1:
distribution['p'] += 1
elif max(max(np.sum(l, 0)), max(np.sum(l, 1))) == 3:
distribution['s'] += 1
else:
distribution['q'] += 1
for k, v in distribution.items():
distribution[k] = float(v)/trial
distribution['p'] = distribution['p']/2.
distribution['q'] = distribution['q']/2.
print 'trial = %d' % trial
print distribution
def exp_c(self):
self.N = int(self.sp.entry[0].get())
self.dla3 = DLA(self.N, view=False)
self.lattice = self.dla3.grow_cluster()
self.view_expansion()
self.plot()
def view_expansion(self):
lattice = self.lattice
center = self.dla3.center
M_b = []
s = np.sum
ave = np.average
append = M_b.append
for k in range(1, center):
nonzero = np.nonzero(lattice[k:-k,k:-k])
tmp = np.array([0])
for i, j in zip(nonzero[0]+k, nonzero[1]+k):
tmp = np.append(tmp, s(lattice[i-k:i+k+1, j-k:j+k+1]))
append(ave(tmp))
self.b = np.array([2.*k+1 for k in range(1, center)])
self.M_b = np.array(M_b)
def plot(self):
fig = plt.figure("Fractal Dimension")
self.ax = fig.add_subplot(111)
self.ax.plot(self.b, self.M_b, '-o')
self.ax.set_xlabel(r'$b$', fontsize=16)
self.ax.set_ylabel(r'$M(b)$', fontsize=16)
self.ax.set_xscale('log')
self.ax.set_yscale('log')
self.ax.set_ymargin(0.05)
fig.tight_layout()
plt.show()
def fitting(self):
if self.b == None:
return
import scipy.optimize as optimize
def fit_func(parameter0, b, M_b):
log = np.log
c1 = parameter0[0]
c2 = parameter0[1]
residual = log(M_b) - c1 - c2*log(b)
return residual
def fitted(b, c1, D):
return np.exp(c1)*(b**D)
cut_from = int(raw_input("from ? (index) >>> "))
cut_to = int(raw_input("to ? (index) >>> "))
cut_b = np.array(list(self.b)[cut_from:cut_to])
cut_M_b = np.array(list(self.M_b)[cut_from:cut_to])
parameter0 = [0.1, 2.0]
result = optimize.leastsq(fit_func, parameter0, args=(cut_b, cut_M_b))
c1 = result[0][0]
D = result[0][1]
self.ax.plot(cut_b, fitted(cut_b, c1, D),
lw=2, label="fit func: D = %f" % D)
plt.legend(loc='best')
plt.show()
def pr(self):
import tkFileDialog
import os
if self.dla is None:
print "first you should run 'a'."
return
fTyp=[('eps flle','*.eps'), ('all files','*')]
filename = tkFileDialog.asksaveasfilename(filetypes=fTyp,
initialdir=os.getcwd(),
initialfile="figure_1.eps")
if filename == None:
return
self.dla.canvas.postscript(file=filename)
if __name__ == '__main__':
Main()
|

